基于综合相关判别的无源航迹关联算法

刘 钊，冯新喜， 周 航，刘玉磊

(空军工程大学信息与导航学院，西安 710077)

0 引言

如何判断来自于两个不同局部节点的两条航迹是否代表同一个目标，是分布式无源多目标跟踪系统的一个重要问题，即航迹与航迹的关联问题，简称航迹关联或者航迹相关问题。对于无源传感器，由于其所探测的每个航迹只对应一个辐射源，而一个目标平台可以装载多个辐射源，因此，如何利用辐射源航迹进行航迹关联，并最终得到正确的目标关联航迹就是难点所在。目前用于航迹关联的算法通常可分为两类［1－3］:一类是基于统计的方法;另一类是基于模糊数学的方法。这些方法都只利用了目标的运动状态信息。事实上，无源传感器不仅仅获取这些信息，还可以获得更多关于目标的其他特征数据(如载频、脉宽、脉幅、到达时间等)［4－5］。关于如何利用这些信息和运动状态信息综合来提高分布式无源多目标系统的航迹关联性能，文献报道上不多见。在此借鉴了文献［6］的思想后将其运用于无源传感器航迹关联上，提出了一种基于综合相关判别的无源航迹关联新方法，即首先利用一个节点获得的综合信息，对来自于一个目标平台的辐射源航迹进行节点内部的自关联，再利用自关联后的结果进行两个节点之间航迹互关联的同时，充分利用无源传感器获取的角度和属性信息建立判别函数，通过关联判决规则进行航迹关联。该算法依据分布的思想对航迹进行关联，并引进了传感器获得的其他特征数据，从而使计算量大大减少，并提高了计算精度。

1 问题描述

令 N1={1，2，…，n1}，N2={1，2，…，n2}分别为节点1和节点2的航迹编号集合，多无源传感器对目标进行联合探测可以有效提高目标的定位精度，获取目标的精确位置信息和属性信息。辐射源探测模型如图1所示。

图1 辐射源探测模型Fig.1 Radiant point exploring model

多无源传感器航迹关联的内容包括:

1)判定一个节点探测到的多个辐射源航迹是否属于同一目标平台;

2)判定两个节点在各自节点内部进行自关联后，所得到的目标航迹是否属于同一目标平台。

内容1)属于一个节点内部的航迹关联问题;内容2)属于多无源传感器之间的航迹互关联问题。无源传感器可以获得辐射源的方位角、俯仰角和丰富的参数信息。通过以上这两步对航迹进行自关联和互关联，可以实现多无源传感器之间的航迹关联。

2 多无源传感器关联算法分析

2.1 一节点内部航迹自关联判别函数

对于一个节点内部的辐射源航迹关联，在判别函数的选取时要充分利用探测到的方位角、俯仰角和辐射源属性信息相结合进行数据关联，这样才能提高航迹自关联的精度。

1)角度信息相关判别函数。

设:θej(li)、αej(li)分别为第 j条航迹的第 li个俯仰角和方位角测量值;θek(li)、αek(li)分别为第k条航迹的第li个俯仰角和方位角测量值;θi=θej(li)－θek(li)，表示第j条航迹的第li个俯仰角和第k条航迹的第li个俯仰角之差;αi=αej(li)－αek(li)，表示第 j条航迹的第li个方位角和第k条航迹的第li个方位角之差。对一个节点的内部航迹进行自关联，其俯仰角和方位角测量误差相同，服从零均值恒定方差的高斯分布，其方差表示为σe，构造统计量为

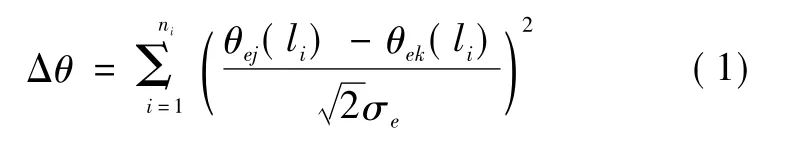
显然，当第j条辐射源航迹与第k条辐射源航迹来源于同一目标平台时，Δθ和Δα都服从均值为0、方差为1的标准正态的抽取子样［1］，且满足一般相似性测量的性质，故将其定义为基于一节点内部航迹的俯仰角和方位角相关判别函数。

2)属性相关判别函数。

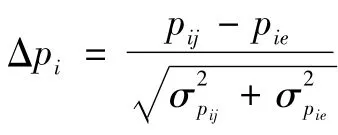
式中:pij表示第j条航迹上的第i个属性信息;pie表示第e条航迹上的第i个属性信息。式(3)满足一般相似性测量的性质，故将其定义为基于一节点内部航迹的属性相关判别函数。

3)综合相关判别函数。

由式(1)～式(3)所得到的表达式均服从正态分布且相互独立，将其综合可以得到

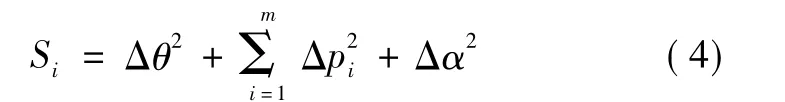
上式服从χ2(n+1)分布，其维数为俯仰角一维，方位角一维，加上属性信息多维构成。

2.2 一节点内部航迹自关联判决规则

当计算出了描述两航迹近似程度的综合相关判别值之后，下一步就是如何判决两航迹间的相似性。为了给出航迹i(i∈N1)与航迹 j(j∈N1)间的相似性判决，将相似度从大到小排序，采用最大判别值识别原则。即若γj*=max(γj)，且γj*＞ε，则在t时刻的航迹i(i∈N1)与航迹 j(j∈N1)关联。ε 为阀值参数，0.5≤ε＜1，可以通过仿真试验确定该值的大小。

为了控制航迹关联检验的完结与终止，可进一步引入航迹关联质量mij(k)。关联质量是关于航迹关联历史情况的度量，其值的大小反映正确关联的可靠程度［8］。若在 t时刻判决航迹 i(i∈N1)与航迹 j(j∈N1)为关联对，则

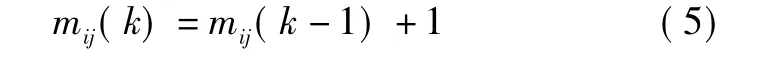
否则

式中，mij(0)=0。如果在t时刻航迹i(i∈N1)与航迹j(j∈N1)第一次关联，mij(t－1)=0，mij(t)=1。为了减少计算量，提高算法的运算速度，当mij≥6时，可以规定航迹i(i∈N1)与航迹j(j∈N1)为固定关联对，并且在后续的检验中，它们不再接受关联检验，直接进入航迹合成阶段。

通过上述的关联判别规则，可以将一个节点内部的来自于同一目标平台的辐射源航迹进行关联，为了在第二步中的两个不同节点间航迹关联，对在一个节点内部的确定为来自同一目标平台的辐射源航迹进行去均值处理，使其合成为一条航迹，反映一个目标平台的运动。

式中，mi为合成后的第i个目标平台的航迹。

2.3 两节点间航迹互关联判别函数

在对每个节点内部属于一个目标平台的辐射源航迹进行关联后，每个节点得到了自己节点探测到的目标航迹，下面的步骤就是要对两个节点得到的目标航迹进行互关联，最后获得多无源传感器的航迹关联结果。

1)角度信息相关判别函数。

设 θdej(li)、αdej(li)为第 d 个节点(d=1，2)的第 j条航迹的第li个俯仰角和方位角测量值;θpek(li)、αpek(li)为第p个节点(p=1，2)的第k条航迹的第li个俯仰角和方位角测量值;θdpi=θdej(li)－θpek(li)表示第d个节点的第j条航迹的第li个俯仰角和第p个节点的第k条航迹的第li个俯仰角之差;αdpi=αdej(li)－αpek(li)表示第d个节点的第j条航迹的第li个方位角和第p个节点的第k条航迹的第li个方位角之差，对两个节点的航迹进行互关联，其方位和俯仰测量误差相对独立，均服从零均值恒定方差的高斯分布［1］，方差表示为σe和σp，构造统计量为

显然，当第d个节点的第j条目标平台航迹与第p个节点的第k条目标平台航迹来源于同一目标平台时，Δθh和Δαh都服从均值为0、方差为1的标准正态的抽取子样，且满足一般相似性测量的性质，故将其定义为基于两节点目标航迹的俯仰角和方位角相关判别函数。

2)属性信息相关判别函数。

式中:phij表示第j条航迹上的第i个属性信息;phie表示第e条航迹上的第i个属性信息。式(10)满足一般相似性测量的性质，故将其定义为基于两节点航迹的属性相关判别函数。

3)综合相关判别函数。

由式(8)～式(10)所得到的表达式均服从正态分布且相互独立，将其综合可以得到

式(11)服从χ2(n+1)分布，其维数为俯仰角一维，方位角一维，加上属性信息多维构成。

2.4 两节点航迹互关联判决规则

关于航迹判决的方法，许多文献均有相关介绍。为了避免大的错误关联概率，可采用双门限关联决策规则［9］，即在选择门限TL的基础上，再设一门限TH，满足TH≥TL，则多节点航迹关联的双门限决策规则为:

1)若Sh≥TH，则判断辐射源航迹i和辐射源航迹j关联;

2)若Sh＜TL，则判断辐射源航迹i和辐射源航迹j有可能关联;

3)若TL≤Sh＜TH，则不确定，需继续进行观测判决。

其中:Sh为根据综合判别函数得出的相似性测度的最大值，即 Sh=max{Shi|i=1，2，…，m};TL为确定的低门限;TH为高门限。TL，TH的确定方法如下:低门限TL确定的原则是使错误拒绝多节点目标平台航迹关联的概率小于预先给定的漏关联概率β，若选择TL=β，则可保证漏关联的概率小于β，故选择低门限TL=β;高门限TH确定的原则是当多节点目标平台航迹is、js本来不关联的情况下，Sh大于TH的概率要小于预先给定的误关联概率α。

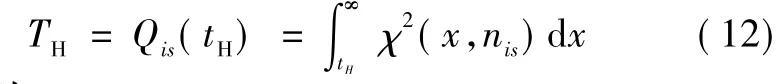
约束条件为

3 算法流程

本文综合相关判别的多无源航迹关联算法步骤如下。

1)设定节点n(n=1，2)的航迹编号集合为

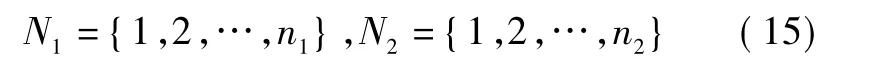
2)对节点n中的每一个节点内部的辐射源航迹进行自关联:

① 选择节点ni，i=1;

② 任取节点n1中的两条辐射源航迹i，j(i≠j)，将两航迹的综合信息代入式(4)，求出综合相关判别函数值;

③若遍历求解完节点n1中的辐射源航迹对后，则 i=i+1(i≤2)，转至②。

3)通过判别规则，依次对节点ni中的辐射源航迹对的判别函数值进行判决，若在t时刻判决航迹i与航迹j为关联对，则

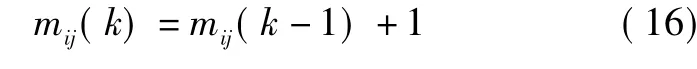
否则

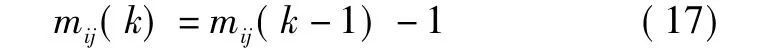
4)当mij≥6时，航迹i与航迹j为固定关联对，并且在后续的检验中，它们不再接受关联检验，直接代入式(7)进行航迹合成;否则，不关联。

5)在4)所合成的目标平台航迹的基础上，对节点n的目标平台航迹进行互关联:

①任取节点n1和n2中各一条目标平台航迹i，j，将两航迹的综合信息代入式(11)，求出综合相关判别函数值;

②若遍历求解完两节点的目标平台航迹对后，进入6);否则转至5)中的①。

6)通过双门限判决规则，对5)中所得判别函数值进行判决，最终获得关联后的航迹。

算法流程如图2所示。

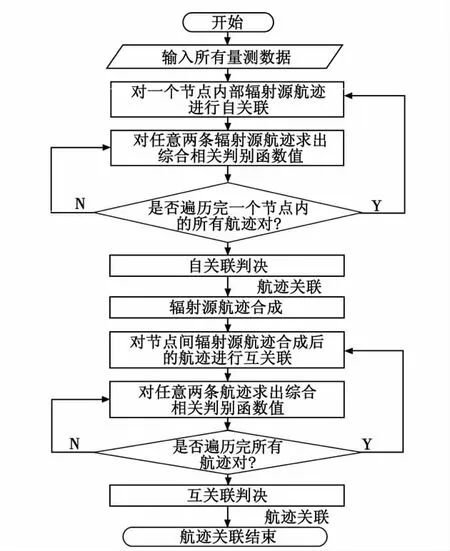
图2 算法的流程图Fig.2 Flow chart of the arithmetic

4 算法仿真与性能分析

仿真考虑两传感器观测3个目标的情况，并且每个目标上面都有两个辐射源。目标1、目标2和目标3均做匀速直线运动，3个目标的6个辐射源的飞行轨迹如图3所示，初始参数如表1所示。

表1 6辐射源的飞行初始参数Table 1 Flight initialization parameters of six radiant points

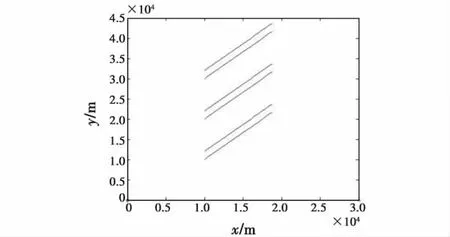
图3 6个辐射源的飞行轨迹示意图Fig.3 The flight contrail pictorial view of six radiant points

传感器1位于(0，0，0，)(单位为 m)，传感器 2位于 (3000，0，0)(单位为m)，传感器1和传感器2的方位角和俯仰角测角误差分别为1.8°和1.6°。

为了验证算法的性能，用蒙特卡罗方法对本文算法进行50次仿真，图4、图5分别为对节点1和节点2探测到的辐射源航迹进行节点内部自关联的正确关联率。为了计算简便，属性相关信息取的是对航迹关联影响最大的3个信息，即工作频率、PRI、脉宽。工作频率的误差 σe1为1 ～1.5 MHz，PRI的误差 σe2为 0.002 ～0.0023 ms，脉宽的误差 σe3为0.002 ～0.0023 μs［10］，在一节点内部航迹自关联判决时，经过试验取阀值参数ε=0.68。

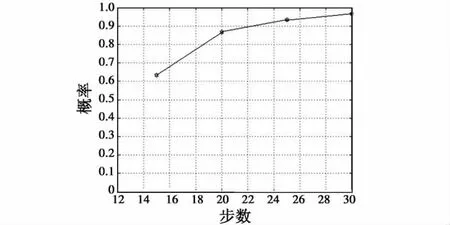
图4 节点1中辐射源航迹正确关联率Fig.4 Correct association rate of radiant point flight path of node 1

图5 节点2中辐射源航迹正确关联率Fig.5 Correct association rate of radiant point flight path of node 2

图6 表示两节点进行互关联的正确关联率，并和加权法进行比较。

图6 综合信息法和加权法关联正确率Fig.6 The integrated correct association rate

表2表示的是综合信息法和加权法正确率的定量比较。

表2 综合信息法和加权法正确率的定量比较Table 2 Comparison of correct association rate of different methods

从仿真实验来看，本文所提的算法能够较为精确地进行多无源传感器的航迹关联，分析图3～图6及表2的结果，可以得到以下结论。

1)在进行各自节点内部自关联时，随着步长的增加，辐射源航迹正确关联率也逐渐增高;在进行两节点间的互关联时，关联正确率也是随着步长的增加而增加，说明此算法能有效进行无源传感器的航迹关联，且正确率较高。

2)综合信息法与加权法进行比较可知，本文所提出的方法，在关联正确率上要远远高于加权法的关联正确率。

5 结束语

针对无源传感器航迹关联的问题，本文提出了一种基于辐射源航迹自关联和目标平台航迹互关联的综合相关判别算法。该算法的特点是，充分考虑到了无源传感器探测目标平台时得到辐射源航迹这一特点，通过辐射源航迹到目标平台航迹两步关联，实现最终的航迹关联，而且该算法充分运用了无源传感器探测得到的角度信息和属性信息，增强了关联的精确度。通过仿真实验表明，该算法能够有效解决多无源传感器的航迹关联问题，并且有较高的关联正确概率。

［1］ 何友，王国宏，彭应宁，等.多传感器信息融合及应用［M］.北京:电子工业出版社，2000.

［2］ 依晓，关欣，何友.分布式跟踪系统的灰色航迹关联模型［J］.信号处理，2005，21(6):653－655.

［3］ LLINAS J，WALTZ E.Multisensor data fusion［M］.Norwood，Massachusetts:Artech House，1990.

［4］ 朱必浩，冯新喜，鹿传国，等.综合利用各类信息的一类灰色航迹关联算法［J］.电光与控制，2011，18(7):22－25.

［5］ 李敬辉，涂拥军，黄高明.舰载被动传感器数据关联算法研究［J］.海军工程大学学报，2008，20(1):44－49.

［6］ 董红波，王刚，刘进忙，等.机载雷达与ESM航迹关联技术研究［J］.传感器与微系统，2010，29(1):12－14.

［7］ 赵海英，黄辉.基于正态分布判别函数的航迹关联门限算法［J］.舰船电子工程，2005，25(6):8－10.

［8］ 颜坤玉，王杰贵，白日辉.基于D－S证据理论的无源航迹关联算法［J］.信息与电子工程，2010，8(5):550－504.

［9］ 杨万海.多传感器数据融合及其应用［M］.西安:西安电子科技大学出版社，2004.

［10］ 王杰贵，罗景青，革学明.无源跟踪中基于灰关联信息融合的概率数据关联算法［J］.电子学报，2006，3(3):391－395.