基于乘性信道的单输入系统均方镇定

沈志萍， 邬依林， 刘 屿

(1.新乡学院数学与信息科学系，河南 新乡 453000; 2.华南理工大学，a.自动化科学与工程学院;b.精密电子制造装备教育部工程研究中心，广州 510640; 3.广东第二师范学院计算机科学系，广州 510310)

0 引言

网络控制系统(Networked Control Systems，NCS)的特征是系统各组件(传感器、控制器、执行器)之间可以通过网络交换信息。在过去几年中，网络控制系统在移动传感器网络、制造系统、遥操作机器人、汽车、航天器等领域已有广泛的应用。物联网产业的兴起和逐渐进入应用阶段，以及计算机、通信和电子技术的飞速发展，为网络控制系统的发展提供了物质准备。例如微型化、智能化传感器的进步，使得价格越来越低、计算机的数据处理能力越来越强;网络技术的不断发展，使得构造的网络控制系统经济且功能强大，足以控制复杂的对象或过程，其应用前景及应用价值将更加诱人，这也是近十年来国内外网络控制系统研究一直十分热门的主要原因。与传统控制系统和控制方法相比，由于网络本身存在着一些信息约束固有本质，如延时、数据传输率和信噪比受限、量化的影响等，使得基于网络控制系统的稳定性条件、性能分析和鲁棒性条件需要重新建立，当前，国内外对这些问题的研究成果主要还集中在系统的稳定性分析上，而对系统性能分析等重要问题的进一步研究正在努力推进中［1－6］。在不同文献中，输入信道的信息约束源于不同形式，如数据传输率［7－8］、量化［9－10］、信噪比受限［11］、延时［12］等。本文将这些源于不同形式信息约束模拟为白噪声随机过程，统一为系统随机不确定性参数来处理，进而得到系统的随机模型，研究具有这种随机模型的网络控制系统的均方可镇定问题，获得均方可镇定的充要条件。其潜在益处在于，不仅可以补充网络控制理论的基本理论和方法，也可以为研究网络控制系统的分析和设计提供一个基本的理论基础。

1 问题的描述

考虑如图1所示的线性时不变离散系统，其系统方程为

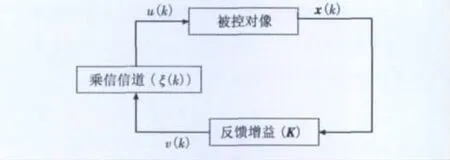
图1 具有乘性信道网络控制系统结构图Fig.1 The structure of networked control system over multiplicative channel

图1 中，输入信道建模成乘性信道ξ(k)，可以是确定性函数或具有某种数理统计特性随机函数。对于文献［10］中的对数量化器而言，输入信道ξ(k)=1+Δ，‖Δ‖≤δ为相对量化误差，ξ(k)是一个非线性的、时变的、具有确定边界的不确定函数，即输入信道模型为一个具有确定扇区边界的函数，文献［10］解决了这种模型信道下系统的均方可镇定问题。不难看出，文献［6］中ξ(k)只是随机函数的一种特例。因此当ξ(k)为具有某种数理统计特性随机函数时，输入信道模型更具一般性和泛化性，本文考虑该种模型下系统均方可镇定时的充要条件。为此，针对ξ(k)提出如下假设。

假设1 ξ(k)为一个离散的白噪声随机过程，具有如下数理统计特性:E{ξ(k)}= μ≠0，var{ξ(k)}=σ2＜ +∞。

定义1随机系统［9］

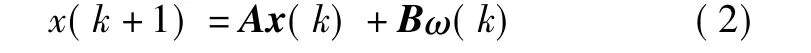
式中，ω(k)为有界随机过程，如果M(k)=E{x(k)x′(k)}对所有的k是适定的，且有，则系统(2)是均方稳定的。

定义2系统(1)中乘性信道ξ(k)的均方容量为

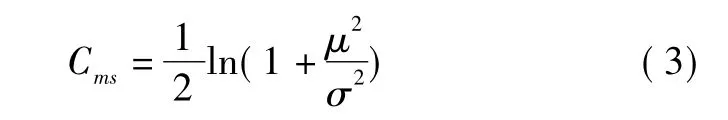
引理1均方小增益定理［14］。对于BS中任意范数有界随机动态系统T1，图2所示的关联系统是均方稳定的充要条件，为:‖T2‖2＜1。

注1:若引理1中T1为随机乘性增益，协方差为，则图2所示的关联系统是均方稳定的充要条件，为:

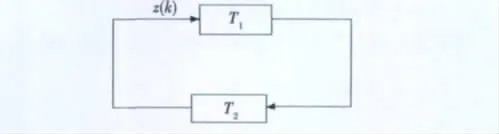
图2 均方小增益定理Fig.2 Mean square small gain theorem

2 主要结果

定理1线性时不变离散系统(1)均方可镇定的充要条件为

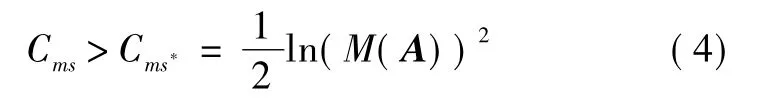
表示A矩阵不稳定的特征值。

证明 系统(1)可重写为

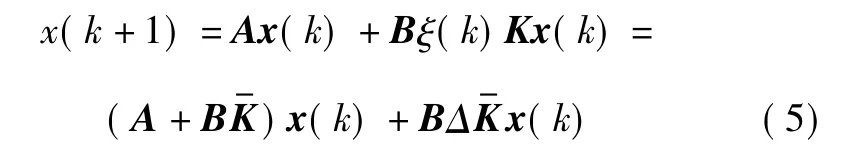
进而，系统(1)可转换为

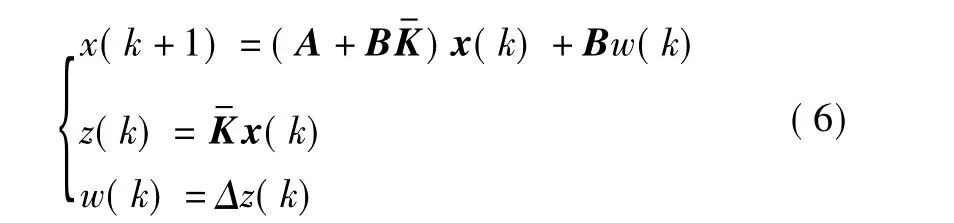
其中，乘性信道模型ξ(k)结构转换如图3所示。

图3 乘性信道转换形式Fig.3 Converted form of the multiplicative channel

而

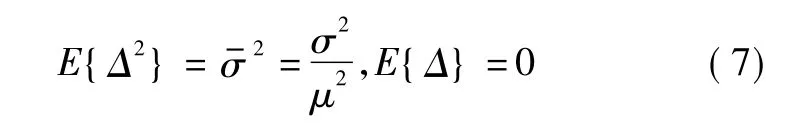
注:真实世界中的白噪声高斯随机过程Δ就可满足式(7)。

进一步，具有乘性信道网络控制系统由图1可转化为图3。

图4中，w(k)到z(k)的传递函数Gzw为

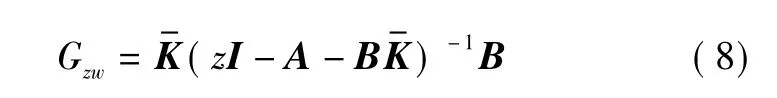
进而

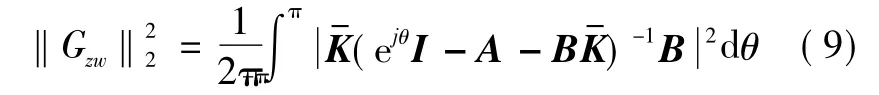
由于图1和图4是等效的，因而系统(1)的均方可镇定性问题可等效为结构图4的均方镇定性问题。

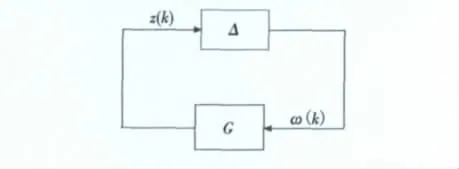
图4 系统结构等效图Fig.4 The equivalent structure of the system

为证明需要，先考虑如下一最小能量LQR控制问题。

考虑如下系统最小能量LQR控制问题

下面采用动态规划方法求解系统(10)最小能量LQR控制问题。设

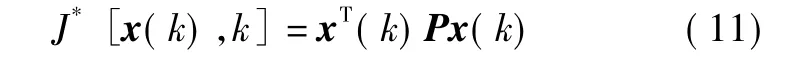
利用经典动态规划法可得

其中，P满足下列Riccati方程。

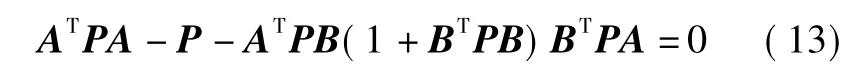
进而，最小能量代价为

对任意x0上述恒成立，当x0=B时，有

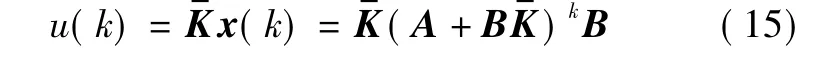
进而将式(15)代入式(10)

由Parseval定理及Fourier变换，式(16)可变换为

由式(9)和式(17)可得

下面来求解J(B)。

不失一般性，假设系统是反稳定的(即系统的特征根均位于单位圆外或单位圆上)，考虑如下系统的能控标准形式。

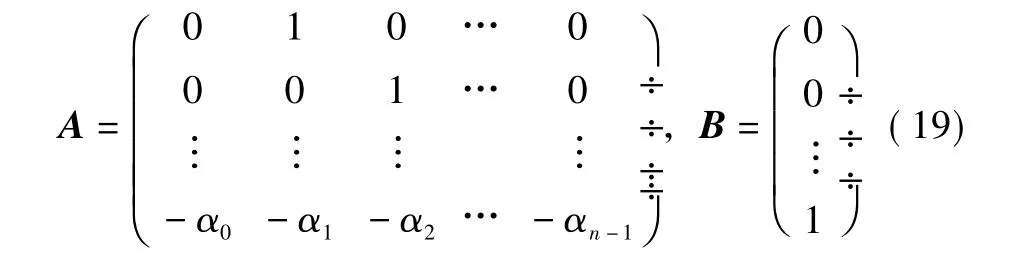
从而

Pnn为P矩阵的第n行、第n列元素(即最后一行、最后一列元素)，且系统开环特征方程为

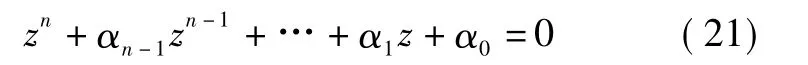
由LQR控制问题［15］可知，可通过设计最优控制器，将系统单位圆外的不稳定的特征根镜像配置到单位圆内，即系统闭环特征方程具有下列形式

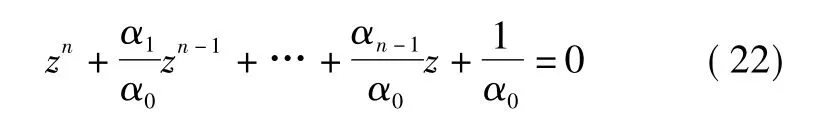
对应的闭环特征矩阵Ac为

从而求得

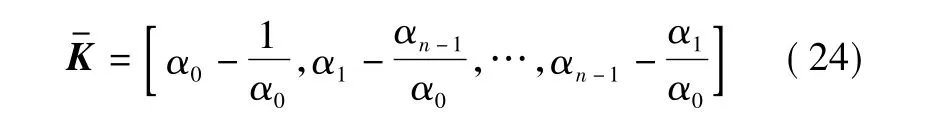
由最小能量控制必在镜像极点上可知

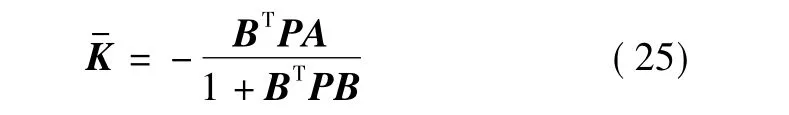
即

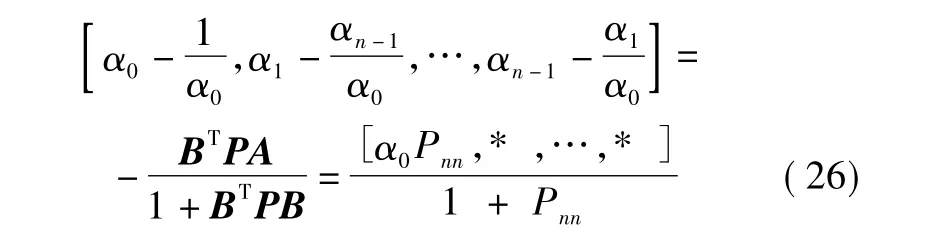
易得

所以由式(18)可得

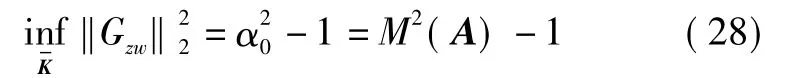
由引理1可知，系统(1)稳定的充要条件是

注2:不等式(29)右边一项为系统Gzw所能容许的随机变量的最大协方差，通常也称为最大均方稳定域度［16］。注3:在证明定理1的过程中，只考虑了系统A反稳定的情形，但对于系统部分特征根稳定情形也同样成立。注4:证明中只考虑了能控标准型;若非能控标准型，可通过等价的坐标变换化成能控标准型。

3 应用

分析各种形式乘性噪声情形下，系统可镇定的充要条件，与现有文献相应问题求解的结论是一致的。

3.1 擦除信道

3.2 扇形边界

4 结束语

本文运用小增益理论、Parseval定理及Fourier变换，将求解基于系统均方可镇定要求的乘性信道均方容量的问题转化为求解一个最小能量LQR控制问题，采用动态规划法和镜像极点配置法，得到了单输入系统情况下，用系统Mahler测度表示的乘性信道均方容量的构成系统均方可镇定的充要条件，并给出了证明。文中用信道容量给出系统可镇定条件，较传统用线性矩阵不等式表示的可镇定条件具有明显的优势，很容易判定系统是否可镇定，给网络工作者带来了方便。

［1］ ZHANG W，BRANICKY M，PHILLIPS S.Stability of networked control systems［J］.IEEE Control Systems Magazine，2001，21(1):84-99.

［2］ HESPANHA J P，NAGHSHTABRIZI P，XU Y.A survey of recent results in networked control systems［J］.Proceedings of the IEEE，2007，95(1):138-162.

［3］ SCHENATO L，SINOPOLI B，FRANCESCHETTI M，et al.Foundations of control and estimation over lossy networks［J］.Proceedings of the IEEE，2007，95(1):162-187.

［4］ ANTSAKLIS P，BAILLIEUL J.Guest editorial special issue on networked control systems［J］.IEEE Transactions on Automatic Control，2004，49(9):1421-1423.

［5］ NAIR G N，FAGNANI F，ZAMPIERI S，et al.Feedback control under data rate constraints:An overview［J］.Proc.IEEE，2007，95(1):108-137.

［6］ HESPANHA J P，NAGHSHTABRIZI P，XU Yonggang.A survey of recent results in networked control systems［J］.Proc.IEEE，2007，95(1):138-162.

［7］ BAILLIEUL J.Feedback coding for information based control:Operating near the data rate limit［C］//Proc.41st IEEE Conf.Decision and Control，Las Vegas，NV，2002:3229-3236.

［8］ NAIR G N，EVANS R J.Exponential stability of finitedimensional linear systems with limited data rates ［J］.Automatica，2003，39(5):585-593.

［9］ ELIA N，MITTER S K.Stabilization of linear systems with limited information［J］.IEEE Transactions on Automatic Control，2001，46(9):1384-1400.

［10］ FU M，XIE L.The sector bound approach to quantized feedback control［J］.IEEE Transactions on Automatic Control，2005，50(11):1698-1711.

［11］ BRASLAVSKY J R，MIDDLETON R H，FREUDENBERG J S.Feedback stabilization over signal-to-noise ratio constrained channels［J］.IEEE Transactions on Automatic Control，2007，52(8):1391-1403.

［12］ NILSSON J.Real-time control systems with delays［M］.Lund，Sweden:Lund Institute of Technology，1998.

［13］ ELIA N.Remote stabilization over fading channels［J］.Systems Control Letters，2005，54(3):237-249.

［14］ JIANBO L，SKELTON R E.Mean-square small gain theorem for stochastic control:Discrete-time［J］.IEEE Transactions on Automatic Control，2002，47(3):490-494.

［15］ KWAKERNAAK H.Linear optimal control systems［M］.New Nork:Wiley，1972.

［16］ BOYD S P，GHAOUI L E，FERON E，et al.Linear matrix inequalities in system and control theory［M］.SIAM Studies in a Applied Mathematics，vol 15，Society for Industrial and Applied Mathematical，Philadelphia，1994.