降雨入渗时沥青路面流固耦合作用的力学响应

吴国雄，周 宇，杨 锐

(1.重庆交通大学土木建筑学院，重庆400074;2.中国水电顾问集团成都勘测设计研究院，四川 成都610072)

流固耦合作用现象越来越受到人们的重视，耦合理论从20世纪70年代正式提出，20世纪80年代后以美国学者Noorishad［1-2］为代表的一批科学家不断加以完善和发展，目前，在工程界已得到广泛应用。沥青路面不仅具有层状特性，而且还是流、气、固三相构成的多孔多相介质。混合料结构微观分析表明，沥青混合料结构层不是连续的均匀介质，而是满布孔隙、裂隙的多孔介质。在实际的渗流过程中，由于孔隙流体压力的变化，一方面要引起多孔介质骨架有效应力变化，如渗透流、孔隙度等变化;另一方面，这些变化反过来又会影响孔隙流体的流动和压力的重分布［3］。因此，对处于潮湿状态的沥青路面在行车荷载作用下考虑渗流场-应力场耦合作用更符合实际。

目前，沥青路面结构力学响应分析中，未考虑孔隙水压力作用，无法模拟车辆荷载作用下骨料变形和孔隙水压的瞬间耦合作用，从而在处理含水沥青路面受力问题时较实际有很大误差。笔者通过软件ABAQUS建立降雨入渗条件下的沥青路面渗流有限元模型，得到了不同降雨历时后沥青路面结构的渗流规律和渗流场的分布状态。在建立合理的降雨入渗初始边界的基础上，采用多孔介质流固耦合理论对沥青路面结构在行车荷载作用下的力学响应进行分析。

1 数值模型的基本控制方程

1.1 降雨入渗条件下多孔介质饱和-非饱和渗流的控制方程

对于雨水入渗，饱和区及非饱和区的地下水运动互相联系，应将两者统一进行研究，即所谓的饱和-非饱和流动问题。应以土水势为因变量，建立统一的控制方程。

以二维情况为例，控制方程为［4］:

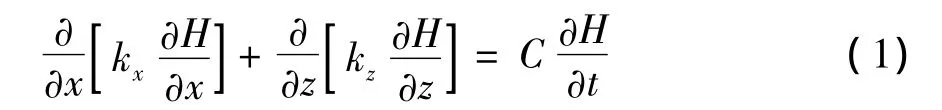
式中:H=h+z(在饱和区，H为饱和流总水头，h为渗透压力水头;在非饱和区，H为非饱和流总水头，h为毛细管压力水头;z为位置水头);kx，kz分别为x和z方向的渗透系数;t为时间;C为比水容，表示单位基质势变化引起的含水量变化，由土水特征曲线的斜率倒数求得。

渗透系数k有如下两种情况:

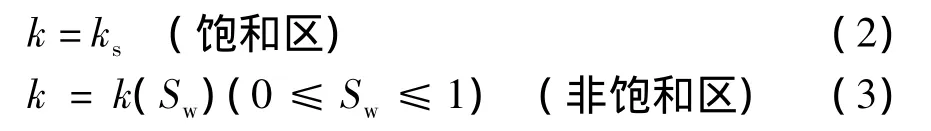
式中:ks为饱和土渗透系数;k(Sw)为非饱和土的渗透系数，Sw随含水率或基质势的变化而变化。

1.2 降雨入渗的多孔介质饱和-非饱和渗流场定解问题

对于降雨入渗的多孔介质饱和-非饱和渗流问题的定解可归纳为［5］:

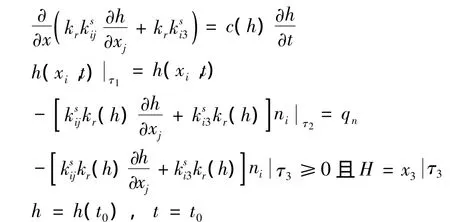
式中:qn为边界τ2上的法向量，向外为正;ni为外法线方向余弦;x3为位置水头;t0为初始时刻;h为渗流域压力水头。

1.3 多孔介质Biot固结基本控制方程

1941年Biot在考虑了土体骨架与孔隙水的相互作用基础上，建立了严格的固结理论。其总控制方程由应力平衡方程、渗流连续方程等组合而成［6］。Biot固结理论考虑了孔隙水压力的变化与土骨架间的相互制约，孔隙水压力和土骨架变形可耦合求解。应力平衡方程为:

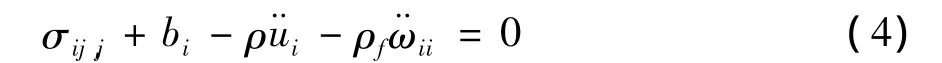
式中:bi为体力分量;¨ui为土骨架加速度;¨ωii为流体的平均相对加速度;ρf为孔隙水密度;ρ为土体的总密度，ρ=nρf+(1-n)ρs(ρs为土颗粒的密度，n 为孔隙率)。

在ABAQUS中，只对固相划分有限元网格，而孔隙水可以在网格中流动。因此，对于孔隙水而言，需要一个连续方程来计算在一定时间增量内，某一点处孔隙水质量的增长率与孔隙水的流速之间的关系。由流体力学的连续性原理，得到渗流连续方程:

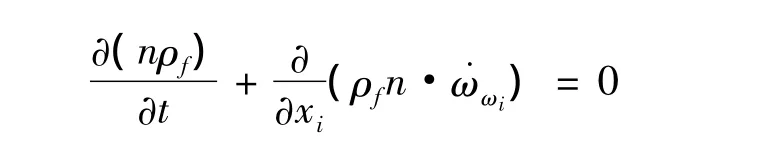
式中:˙ωωi为孔隙水相对于固体颗粒的流速。

2 分析方法与有限元模型的建立

2.1 分析方法

目前，针对沥青路面结构在荷载与水耦合作用下沥青路面结构的数值分析，都是将沥青路面结构层视为完全饱水的最不利状态进行分析。为了与实际降雨入渗后路面内部水分的分布状态更加接近，笔者建立了降雨入渗条件下的沥青路面渗流有限元模型，得到不同降雨历时后沥青路面结构的渗流规律和渗流场的分布状态。在得到合理初始渗流场的条件下，建立动态车载作用下的沥青路面结构耦合分析有限元模型，更加符合实际水环境下的沥青路面相关力学响应分析，具体的分析步骤如图1。

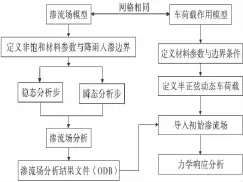
图1 基于降雨渗流分析的沥青路面渗流场-应力场耦合作用分析步骤Fig.1 Analysis steps of asphalt pavement coupled seepage and stress field which based on analysis of rainfall infiltration

2.2 有限元模型的建立

2.2.1 几何模型

为了保证有限元计算精度的同时，避免增加过多的计算工作量，分析采用的沥青路面结构的模型尺寸为 3.5 m ×3.5 m(图2)，其中，面层采用4 cm SMA-13沥青混凝土+6 cm AC-16沥青混凝土+8 cm AC-20沥青混凝土，基层为36 cm水泥稳定碎石，底基层为20 cm级配碎石，土基为砂质壤土(图3)。

图2 轮载作用下沥青路面流-固耦合分析有限元模型Fig.2 Finite element model of asphalt pavement under wheel load fluid-solid interaction

图3 沥青路面各层次参数Fig.3 Parameters of layers in asphalt pavement

2.2.2 边界条件的确定

模型的边界条件为:左右两侧边界为横向固定，竖向自由的不透水边界;下边界水平和竖向均为固定的不透水边界，即认为距路面以下足够深处，竖向和径向位移均为0;上边界在除车轮作用除外均为透水边界。在进行降雨渗流分析时将路表面设为降雨边界，即fp=q。当q大于上面层的饱和渗透系数时，将此边界设定为定水头边界H=z，当降雨停止后，路面设定为自由边界;路基底部设定为不透水边界，模型两侧边界设定为流量等于0的边界。此外，渗流分析时不考虑蒸发的影响。

2.2.3 其他计算参数的确定

采用具有恢复时间的半正弦波瞬态荷载来模拟实际路面所承受的车辆动态作用。饱和渗流中材料的渗透传导系数(k)不随孔隙水压力(p)的变化而变化，为饱和渗透系数(ks)。参考文献［7-8］，得到了沥青各面层、基层、土基的饱和渗透系数，如表1。在非饱和渗流中，多孔介质的渗透系数随基质吸力的变化有很大的改变，本文中多孔介质的渗透系数采用 R.G.Mein［9］所研究的计算公式来定义渗透系数和基质吸力的关系并参考文献［10］的计算结果。

表1 各层材料饱和渗透系数Table 1 Saturated hydraulic conductivity layers of materials /(m·s－1)

3 降雨入渗条件下渗流规律分析

为了对降雨入渗至沥青路面结构各层的规律进行更为详细的了解，选取有限元网格模型中各层的中间节点的计算结果进行分析，计算结果如图 4、图 5。

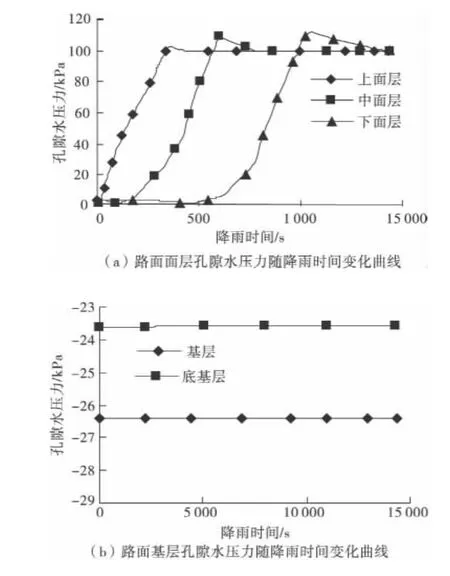
图4 路面各结构层孔隙水压力随降雨时间变化曲线Fig.4 Pore pressure of the road structures changing with the time during the rainfall

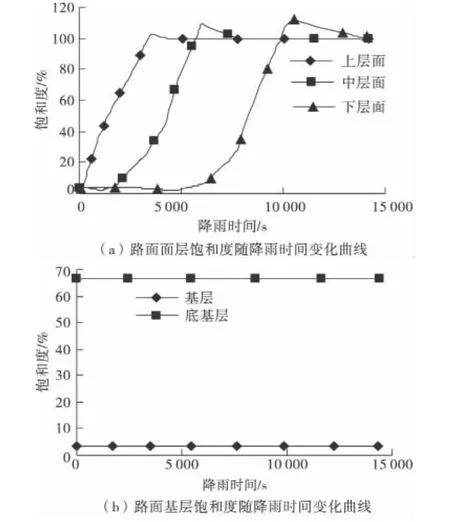
图5 路面各结构层饱和度随降雨时间变化曲线Fig.5 Saturation of the road structures changing with the time during the rainfall

由图4、图5可见，在4 h的降雨过程中，各面层结构降雨入渗有着相似的规律。在降雨初期，饱和度随着降雨的历时延续而显著的提高，随后饱和度会有所下降，然后逐渐趋向稳定，并且由上至下，各面层逐步达到完全饱和状态，孔隙水压力也随着时间的增加而逐步提高，由初始状态下的基质吸力变化为正的水压力。而在4 h的降雨历时中，由于水泥稳定碎石基层的渗透系数与面层材料相比有数量级的差别，故而基层材料对下渗的水流起到了暂时阻挡的作用，故基层和底基层保持初始的非饱和状态不变。由此可见，降雨入渗过程对沥青路面特别是面层结构影响显著。

4 流固耦合作用下力学响应分析

沥青路面常出现的破坏模式主要包括沉陷、车辙、疲劳开裂、泛油、推移和拥包、松散与坑槽等［7］。而沥青路面在复杂水环境下发生损坏的模式的原因［8］并不单一，各种水损坏对路面的使用性能有不同性质和程度的影响。笔者选取较为关注的孔隙水压力、孔隙水流速、各结构层层底最大主应力及剪应力作为研究对象，选取路面结构在降雨7 200 s后的渗流场作为初始边界条件，对其在动态车荷载作用下的变化规律进行分析，结果如图6。

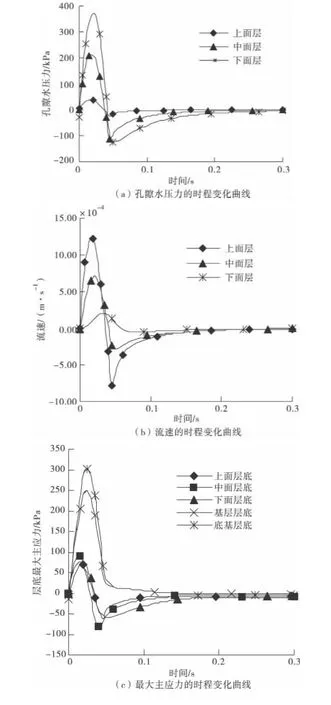
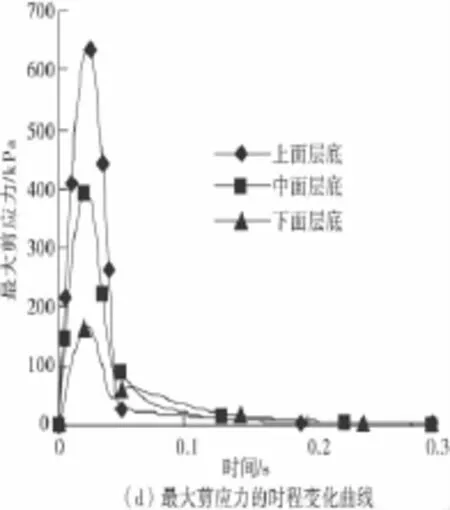
图6 各计算指标的时程变化曲线Fig.6 Time history curve of parameters

分析图6可知:

1)在整个车辆荷载作用过程中，孔隙水压力和孔隙水流速同样具有波的传播特性。孔隙水压力与水的流速均出现了较大的正、负逆转，这一过程反映了处于潮湿状态沥青路面在行车荷载作用下其内部先后产生正负压的泵吸作用与反复冲刷过程。

2)车辆荷载作用下，沥青面层内部的孔隙水压力随着深度的增加而增加，正向与负向的孔隙水压力最大值均出现在下面层底部，分别达到387 kPa和－113 kPa;上面层的孔隙水压力为最小值，分别为35 kPa和－10 kPa，二者位置不同，孔隙水压力的最大值差距超过10倍;而孔隙水的流速却随着深度的增加而减小，最大的正向与负向的孔隙水流速出现在上面层，上面层与下面层的孔隙水流速最大值差距同样也有近6倍。

3)考虑水和动态荷载耦合作用时，路面结构内部的应力状态同样存在波动特性，基层与底基层始终处于受拉状态，而沥青面层整个加载过程中承受了拉、压应力的反复作用。一旦材料所受到的最大拉应力超过极限拉应力值，将导致开裂破坏。

5 结论

分析了降雨入渗条件下沥青路面的渗流规律，及沥青路面流固耦合作用下的力学响应规律，得到了以下主要结论:

1)在降雨入渗初期，饱和度随着降雨的历时延续而显著的提高，随后饱和度会有所下降，并逐渐趋向稳定，同时，由上至下，各面层逐步达到完全饱和状态;孔隙水压力也随着时间的增加而逐步提高，由初始状态下的基质吸力变化为正的水压力。

2)动态车荷载作用过程中，孔隙水压力与流速均出现了较大的正、负逆转，这一过程反映了处于潮湿状态沥青路面在行车荷载作用下，其内部先后产生正负压的泵吸作用与反复冲刷过程，并且孔隙水压力与水的流速最大位置分别位于沥青面层的底层与上层。此外，在水与荷载的动态耦合作用下，结构层层底主应力与剪应力均呈现波动特性。

［1］ Noorishad J.Coupled thermal-hydraulic-mechanical phenomena in saturated fractured porous rocks:numerical approach［J］.Geophysical Research，1989，89(B12):65-73.

［2］ Oda M.Permeability tensor for discontinuous rock masses［J］.Geotechnique，1985，35(4):483-495.

［3］ 董平川，徐小荷，何顺利.流固耦合问题及研究进展［J］.地质力学学报，1999，5(1):17-26.

Dong Pingchuan，Xu Xiaohe，He Shunli.Fluid-solid coupling problem and research progress ［J］.Journal of Geomechanics，1999，5(1):17-26.

［4］ 王彦.降雨入渗对边坡稳定的影响［D］.南京:河海大学，2001.

［5］ 戚国庆，黄润秋，速宝玉，等.岩质边坡降雨入渗过程的数值模拟［J］.岩石力学与工程学报，2003，22(4):625-629.

Qi Guoqing，Huang Runqiu，Su Baoyu，et al.Rock slope of the process of rainfall infiltration numerical simulation［J］.Journal of Rock Mechanics and Engineering，2003，22(4):625-629.

［6］ 岳庆霞，李杰.软件ABAQUS在饱和土体动力响应分析中的应用［J］.地震工程与工程振动，2006，26(3):238-241.

Yue Qingxia，Li Jie.ABAQUS software in the saturated soil dynamic response analysis of application［J］.The Earthquake Engineering and Engineering Vibration，2006，26(3):238-241.

［7］ 刘明.路面结构排水特性的非饱和渗流数值模拟与分析［D］.长沙:湖南大学，2007.

［8］ 李亮.路面结构在降雨条件下的非饱和渗流分析及排水性能评估［D］.长沙:中南大学，2009.

［9］ Mein R G.Modeling infiltration during a steady rain［J］.Water Resource Research，1973，9(2):384-393.

［10］杨锐.沥青混凝土非饱和状态渗流场-应力场耦合作用下疲劳破坏研究［D］.重庆:重庆交通大学，2011.