基于改进遗传算法的敏捷卫星姿态路径规划

刘富钰， 崔培玲

0 引言

从航天应用需求分析可知，很多航天任务要求卫星具有快速姿态机动能力，此类卫星称为敏捷卫星。利用敏捷姿态机动能力，在测绘领域可实现同轨立体成像;在空间对抗领域，可实现攻击载荷的快速瞄准，提高快速反应能力。世界各航天大国意识到敏捷卫星快速机动所具有的战略价值，都纷纷发展敏捷卫星。国际上具有敏捷姿态机动能力的代表性卫星有Pleiades，IKonos，Bilsat，WorldView等。快速姿态机动控制作为敏捷卫星的关键技术之一，日益为学者们所关注。控制力矩陀螺(Control Moment Gyro，CMG)因其输出力矩大、响应速度快等优点，成为敏捷卫星实现快速机动的理想执行机构［1］。相比单框架 CMG，双框架 CMG(Double Gimbal CMG，DGCMG)具有操纵奇异问题不突出，能够提供最多的控制自由度，系统冗余性好，可用最少的单机实现航天器的三轴姿态控制等优点［2］。早在20世纪70年代，国外DGCMG已进入工程应用阶段。三正交安装的DGCMG被成功应用于空天实验室(Skylab)［3］;而目前在轨的国际空间站(ISS)采用了四平行构型的 DGCMG［4］。

目前基于CMG的航天器姿态控制已经有一些研究成果［5－7］。现有的姿态控制系统通常是将控制律和操纵律独立设计。控制律在计算指令力矩时并不考虑可能带来的CMG奇异问题，将奇异问题的避免和逃离完全交予操纵律处理，这样难以从全局的角度对CMG的奇异问题进行回避。而一种有效的奇异回避方法是在整个机动过程中考虑航天器和CMG的综合模型进行路径规划［8－9］。此外，在卫星大角度姿态机动的任务中，如果直接使用常规的控制器进行控制，由于初始的误差较大，容易造成执行机构饱和，并且不容易实现初末角速度均不为零的机动。因此，需要对敏捷卫星机动的路径进行规划，使其在快速完成机动任务的同时，尽量避免CMG系统陷入奇异状态。文献［8－9］将应用单框架CMG的卫星姿态路径规划问题转换为最优控制问题，再分别采用Legendre伪光谱和傅里叶基变换的方法进行求解。但是，它们获得的路径均为局部最优解［10］。

由于遗传算法不受求解空间的限制，不必要求连续性、导数存在和单峰等假设，以及其固有的并行性，使其在路径规划问题上得到广泛的研究［11－13］。但传统遗传算法仍存在诸如搜索时间长，易陷入局部最优等缺点。针对这些缺点，文献［14－15］提出了具有自适应变化交叉概率和变异概率的遗传算法。此外，文献［11－13］在进行路径规划时只要求路径本身平滑，不要求其导数平滑。而在基于DGCMG的敏捷卫星的机动过程中，为了保证DGCMG的安全运行，要求指令力矩平滑，即要求姿态机动路径的一阶导数和二阶导数平滑。

本文研究了一种改进的遗传算法对基于DGCMG的敏捷卫星的姿态路径进行离线规划，为姿态跟踪控制器进行跟踪控制完成整体姿态机动任务打下基础。根据敏捷卫星姿态机动的特点，采用启发式方法生成初始种群，从而提高遗传算法的搜索效率;然后，在考虑控制输入有界、执行机构饱和、奇异测度约束和星体角速度限制等约束的同时，将DGCMG消耗的能量作为适应度函数，从而保证 DGCMG的安全运行，使DGCMG远离奇异状态;同时，引入了自适应交叉率和变异率的方法，较好地处理传统遗传算法在全局搜索性能和收敛速度之间的矛盾;并根据敏捷卫星姿态机动路径的一阶导数和二阶导数平滑的要求，对星体角速度及其角加速度提出平滑变异算子。

1 基于DGCMG的敏捷卫星动力学模型

1.1 卫星动力学建模

本文采用基于误差四元数的卫星运动学模型和动力学模型，定义卫星本体系相对于惯性系的姿态四元数为{q0(t) q(t)}，期望姿态四元数为{qd0(t) qd(t)}。误差四元数{qe0(t) qe(t)}为

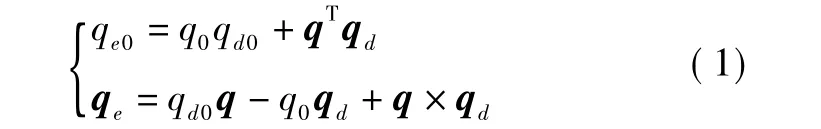
DGCMG通过改变其转子的角动量方向产生所需的控制力矩，定义hcmg为DGCMG的总角动量，根据角动量定理，DGCMG的输出力矩为

由于一般敏捷卫星的刚性较好，不考虑其柔性特性，则根据欧拉定理可得到基于误差四元数的卫星运动学和动力学模型分别为［16］

式中:J为卫星的转动惯量矩阵;u=Tcmg∈R3为指令力矩;Td∈R3为干扰力矩。

1.2 DGCMG构型及奇异性描述

为了实现敏捷卫星的三轴姿态控制，本文选择2个DGCMG组成的正交构型。其构型坐标如图1所示。

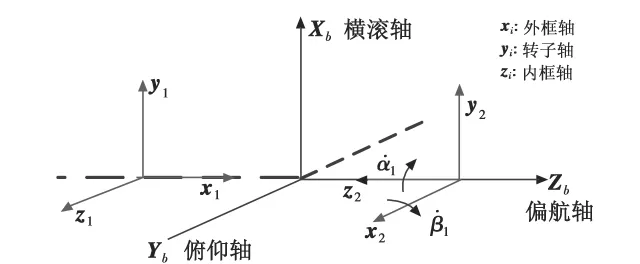
图1 2－DGCMG正交构型示意图Fig.1 Two DGCMG orthogonal configuration

图1中:Xb、Yb和Zb为沿卫星本体系3个坐标轴的单位向量，三者相互正交;xi、yi和zi分别为沿第i个DGCMG的外框架轴、转子轴和内框架轴的单位向量(i=1，2);αi为第 i个 DGCMG 的内框架角;βi为第i个DGCMG的外框架角;令h0为DGCMG角动量大小。根据坐标系定义，DGCMG系统的角动量在本体系的三轴分量为

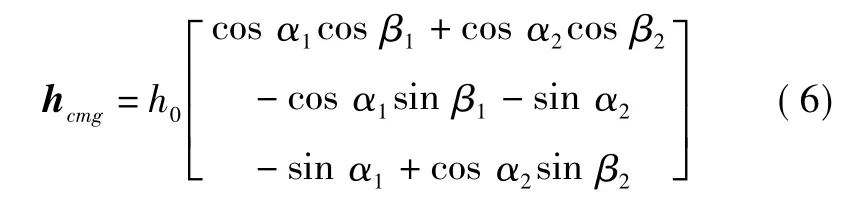
通过式(6)可以得到2－DGCMG正交构型DGCMG输出力矩表达式为

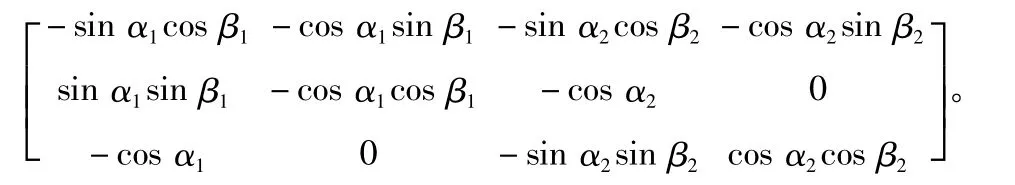
所谓奇异问题是指DGCMG在某种框架角向量δ的配置下，所能提供的力矩正交于期望的控制力矩，失去在该方向的输出力矩能力。表示奇异程度大小的奇异度量为［16］

式中，d为大于零的标量，d=0表示DGCMG系统完全陷入奇异状态，d越大表明DGCMG系统距奇异状态越远。

2 基于改进遗传算法的敏捷卫星姿态路径规划

为了提高遗传算法的搜索效率，本文采用浮点数编码，并结合敏捷卫星大角度姿态机动的特点，采用启发式方法生成初始种群;然后，在考虑敏捷卫星多种物理限制的同时，以DGCMG消耗的能量作为适应度函数，从而保证DGCMG的安全运行，使DGCMG远离奇异状态;同时，引入自适应交叉率和变异率的方法，并针对基于DGCMG敏捷卫星姿态路径的一阶导数和二阶导数平滑的要求，对星体角速度及其角加速度提出平滑变异算子。

1)染色体的编码。

二进制编码是遗传算法最为常用的编码方式，但二进制编码过于冗长，降低了搜索效率，并不适用于路径规划。浮点数编码相对于二进制编码更适合解决多维问题，且具有精度高、实现简单、计算量小等优点［11］，因此，本文采用浮点数编码。其结构为(qe，1，qe，2，…，qe，n)，其中 qe，1和 qe，n分别表示起始姿态和目标姿态四元数的矢量部分，qe，i(i=1，2，…，n －1)表示路径上除两端点以外某一中间点的姿态四元数矢量部分。路径长度n通过仿真时间，即根据卫星的机动能力指标确定出的期望机动时间T和仿真步长Ts进行确定，n=T/Ts。

2)初始种群的确定。

针对传统遗传算法随机生成初始种群所带来的搜索效率低等缺点，本文采取启发式方法生成初始种群。首先根据已知的路径起始点 qe，1，目标点 qe，n，星体的初始角速度ω0，期望角速度ωd和期望角加速度结合动力学模型求出 qe，2，qe，n－2和 qe，n－1。qe，3到 qe，n－3由以下几种规则生成初始种群。

①为了使能量趋于最小，qe→0是一个单调递增或递减的过程，本文基于此启发式地产生部分初始种群。具体为

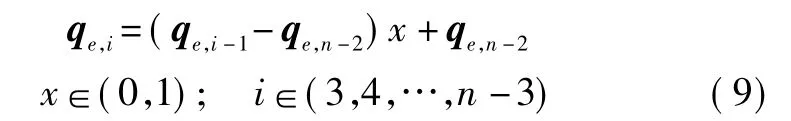
② 由于 qe，2和 qe，n－2已知，如果不考虑奇异点，这两点的连线是长度最短、最平滑的一条路径，本文基于此启发式地产生部分初始种群。

③由于最快的卫星姿态大角度机动速度变化通常包括加速和减速阶段，且S型函数导数的曲线与此相似。因此，本文基于此启发式地产生初始种群，具体为

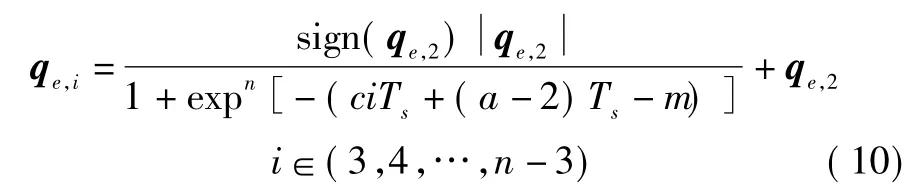
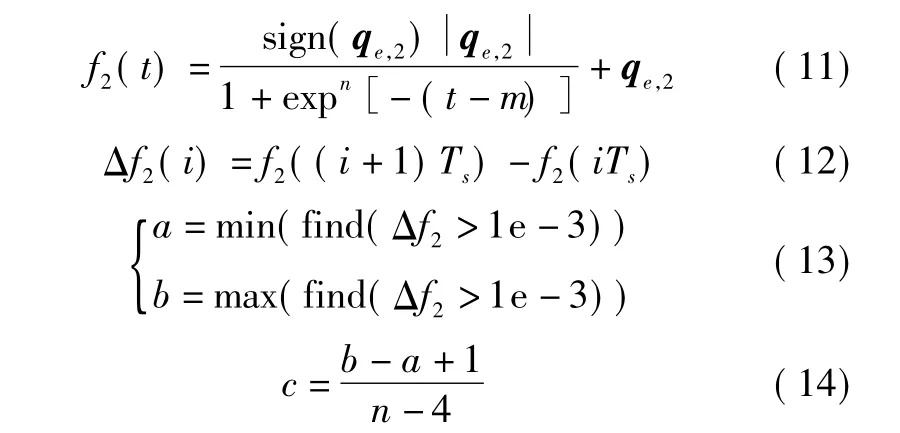
式中，t∈(0，Ta)，Ta为大于 T的一个适当的数。

3)适应度函数选取。

现存的操纵律，如广义鲁棒伪逆操纵律，在避免奇异时通常会引入CMG框架的空转运动。而这些空转运动将增加CMG消耗的能量。因此，为了保证DGCMG的安全运行，使DGCMG远离奇异状态，将DGCMG消耗的能量作为适应度函数。通常，人们采用控制输入的范数估计消耗的能量。但由于敏捷卫星的角速度较大，相对DGCMG的框架角速度不容忽视，因此仅用控制输入的范数不能准确地估计DGCMG消耗的能量。采用式(15)对DGCMG消耗的能量进行估计。

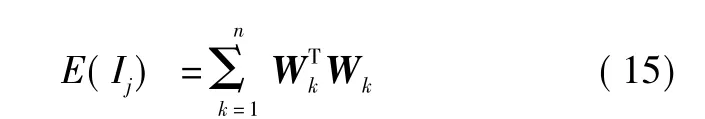
实际应用中，敏捷卫星受到多种物理限制，如控制输入有界、执行机构饱和、奇异测度约束和星体角速度限制，分别被描述为

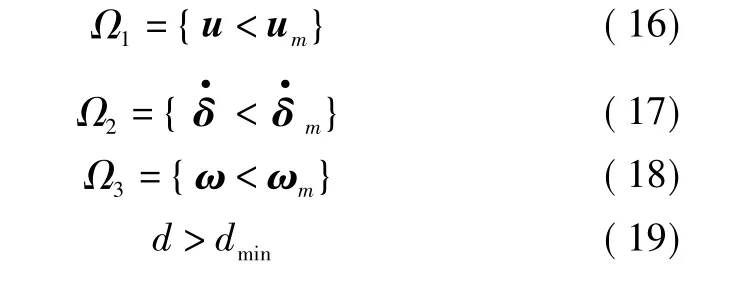
为了在满足敏捷卫星多项约束条件的同时，又使得DGCMG消耗的能量最小，设计适应度函数为

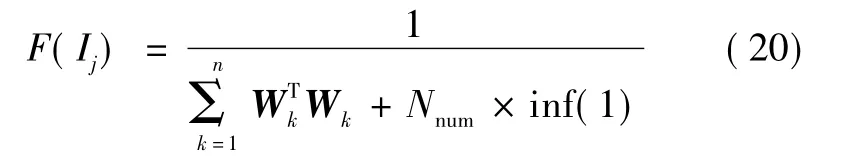
式中:Nnum为路径Ij的不可行点数，即超出各种物理限制点的总数，若Nnum=0，表示Ij为可行路径;inf(1)为一个适当的正数。式(20)表示当路径Ij不可行时，在其总能量上施加惩罚项。

4)遗传操作。

交叉概率和变异概率在整个进化过程中保持不变，是导致遗传算法性能下降的重要原因。为了提高种群的多样性，保证算法的收敛性和快速性，本文引入了自适应交叉率和变异率的方法。并且，针对基于DGCMG敏捷卫星姿态路径的一阶导数和二阶导数平滑的要求，对星体角速度及其角加速度提出平滑变异算子。

选择:采取的选择算子直接将适应度函数值最大的N/2个个体选入下一代，N为种群规模。

交叉:交叉算子产生的子代由两部分组成:第一部分等于选择算子选择的N/2个个体;第二部分由选择算子选择的N/2个个体作为父代交叉而成。本文采取如文献［11］所示的交叉过程。

遗传算法的参数中交叉概率和变异概率的选择是遗传算法行为和性能的关键所在，直接影响算法的收敛性能。本文采取如下自适应交叉率［14］

式中:g表示遗传代数;G表示最大遗传代数。

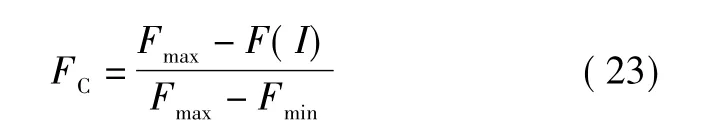
式中:Fmax表示最大适应度值;Fmin表示最小适应度值;表示平均适应度值;F(I)取F(Ii)和F(Ij)之间的较

大值;Ii和Ij为两个待交叉的个体。通过分析不难看出，这种交叉率能够保证在迭代初期，交叉率较大，从而加快进化的速度，避免遗传算法陷入迟钝状态。同时，它还能保证在迭代后期，交叉率较低，并逐步减小至一常量，从而保证平滑收敛。

变异:执行变异算子时，先在路径中随机选择一个除起始点 qe，1，目标点 qe，n和由初始条件计算的 qe2、qen－2和 qen－1以外的节点，再根据选中的随机数找到相应的节点位置，选定后进行变异操作。采取的自适应变异率［15］为

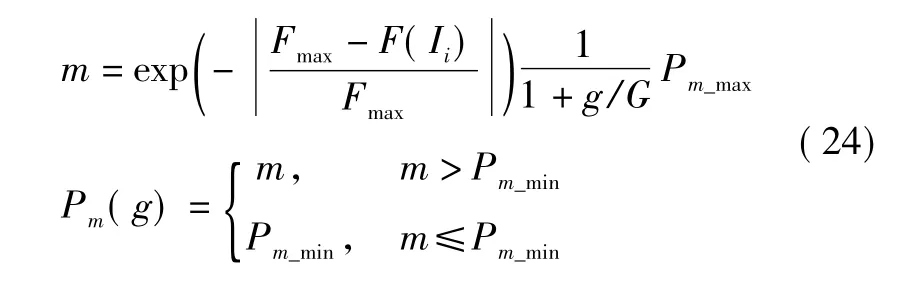
式中，Pm_max为预设置的最大变异概率;Pm_min为预设置的最小变异概率;Pm(g)为g代种群个体Ii的变异概率。随着遗传代数g的增加，此种变异概率能逐渐减小，从而使得种群迅速集中。另外，对于劣质个体，变异率会较大，而优秀个体的变异率会较小。

由于姿态机动过程中要求星体角速度和指令力矩都尽量平滑，因此针对星体角速度及其角加速度提出了平滑变异算子。具体思想是将某个比它相邻两点均小(大)的路径点变异在其相邻两点之间。星体角加速度的平滑变异算子与星体角速度的平滑变异算子类似。这里仅以星体角速度的平滑变异算子进行说明。若路径Ii的星体角速度处于上升阶段，且第k点比其相邻两点均小(大)，采用如式(25)进行变异。

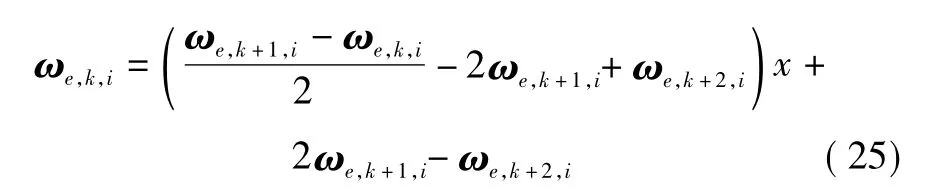
式中:x∈(0，1);ωe，k，i为路径 Ii第 k 点的误差角速度。

若路径Ii的星体角速度处于下降阶段，且第k点比其相邻两点均小(大)，则采用式(26)进行变异。

式中，x∈(0，1)。

在变异操作中，变异可能会使一些优秀个体被破坏掉，无法进入下一代。因此本文采用优秀个体保护法，即保留上一代最优秀的个体，使之直接进入下一代，这样可增加算法的收敛性。

3 仿真结果分析

遗传算法的种群规模为100个，最大遗传代数为2000，最大变异概率为Pm_max=0.08，最小变异概率为Pm_min=0.03。

将两种方法各运行10次，从中随机选出3组解作为示例。图2～图7给出了第1组仿真结果。

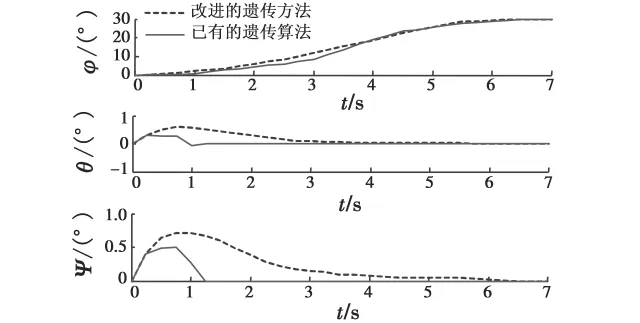
图2 姿态角Fig.2 Euler angle

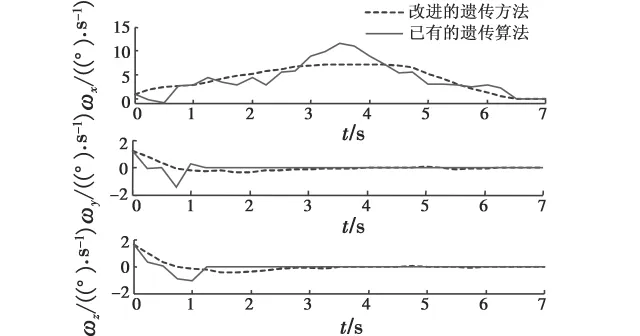
图3 星体角速度Fig.3 Angular velocity

图4 指令力矩Fig.4 Command torque

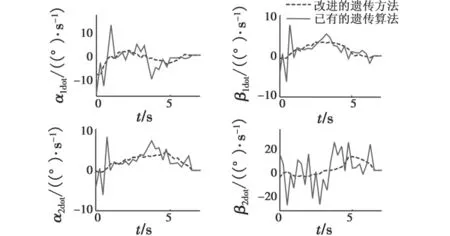
图5 DGCMG框架角速度Fig.5 Gimbal angle velocity of DGCMG

图6 DGCMG框架角Fig.6 Gimbal angle of DGCMG

图7 奇异测度Fig.7 Singularity measurement

从图2可以看出，由于路径的起始点和目标点是给定的，无论是改进的遗传算法还是已有遗传算法，都能到达目标姿态。从图3～图5可以看出，已有遗传算法的星体角速度、指令力矩和框架角速度均超出了约束限制，且抖振较大;而采用本文方法得到的仿真结果均满足约束限制，且曲线较为平滑。从图7可以看出，两种方法的奇异测度均高于奇异测度约束，而本文方法得到的最小奇异值高于已有遗传算法得到的最小奇异值。

表1 采用已有遗传算法的3组仿真结果Table 1 Three groups of simulation results using the existing genetic algorithm

表2 采用改进遗传算法的3组仿真结果Table 2 Three groups of simulation results using the improved genetic algorithm

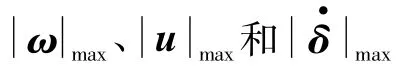
由此可见，在控制输入有界、执行机构饱和、奇异测度约束和星体角速度限制等多种约束下，本文方法能够规划出满足机动能力指标且能量较优的有效路径。

4 结束语

对于以DGCMG作为执行机构的敏捷卫星，在其大角度姿态机动任务中，若直接采用常规控制器进行姿态控制，存在容易造成执行机构饱和，难以从全局角度回避CMGs的奇异等问题。针对此问题，本文研究了一种改进的遗传算法对基于DGCMG的敏捷卫星的姿态路径进行离线规划，为姿态跟踪控制器进行跟踪控制、完成姿态整体机动任务打下基础。本文采用浮点数编码，并结合敏捷卫星大角度姿态机动的特点，采用启发式方法生成初始种群，从而提高算法的搜索效率。在考虑敏捷卫星受到的多种物理限制的同时，以DGCMG消耗的能量作为适应度函数，保证DGCMG远离奇异点。引入了自适应交叉率和变异率的方法，从而提高种群的多样性，保证算法的收敛性和快速性。并对星体角速度及其角加速度提出平滑变异算子以保证卫星的星体角速度和指令力矩平滑。最后，利用该算法进行敏捷卫星姿态路径规划的数值仿真。仿真结果表明，在控制输入有界、执行机构饱和、奇异测度约束和星体角速度限制等多种约束下，以本文算法寻求的路径较好地满足了机动能力指标，且能量较优。

［1］ LAPPAS V J.A Control Moment Gyro(CMG)based Attitude Control System(ACS)for agile small satellites［D］.Guildford:University of Surrey，2002.

［2］ 汤亮，陈义庆.双框架控制力矩陀螺群的建模与分析［J］.航空学报 ，2008，29(2):424－429.

［3］ KENNEL H F.A control law for double－gimbaled control moment gyros used for space vehicle attitude control［R］.NASA TMX－64536，1970.

［4］ BONG W.Singularity escape/avoidance steering logic for control moment gyro systems ［J］.Journal of Guidance，Control，and Dynamics，2005，28(5):948－956.

［5］ BONG W.Rapid multitarget acquisition and pointing control of agile spacecraft［J］.Journal of Guidance，Control，and Dynamics，2002，25(1):96－104.

［6］ HEIBERG C J，BAILEY D.Precision spacecraft pointing using single－gimbal control moment gyroscopes with disturbance ［J］.Journal of Guidance，Control，and Dynamics，2000，23(1):77－85.

［7］ BUKHAR H Z，BHATTI A I，AFTAB M F，et al.Multi－objective controller for Control Moment Gyro(CMG)using LMI［C］//Islamabad:International Bhurban Conference on Applied Sciences ＆ Technology，2009:203－206.

［8］ 刘刚，李传江，马广富，等.应用SGCMG的卫星姿态快速机动控制［J］.航空学报，2011，32(10):1905－1913.

［9］ KUSUDA Y，TAKANASHI M.Design of feedback control system using nominal inputs for satellite attitude maneuver using control moment gyros ［J］.Journal of Guidance，Control，and Dynamics，2011，34(4):1209－1218.

［10］ RAO A V.A survey of numerical methods for optimal Control［J］.Advances in the Astronautical Sciences，2009，135(1):497－528.

［11］ TIAN L F，COLLINS C.Motion planning for redundant manipulators using a floating point genetic algorithm［J］.Journal of Intelligent and Robotic Systems，2003，38:297－312.

［12］ 鲁艺，吕跃，罗燕，等.基于遗传算法的UAV航迹规划［J］.电光与控制，2012，19(1):29－33.

［13］ OSCAR C，LEONARDO T，PATRICIA M.Multiple objective genetic algorithms for path－planning optimization in autonomous mobile robots ［J］.Soft Computing，2007，11:269－279.

［14］ 王岚.基于自适应交叉和变异概率的遗传算法收敛性研究［J］.云南师范大学学报，2010，30(3):32－36.

［15］ 欧阳森，王建华，耿英三，等.一种新的改进遗传算法［J］.计算机工程与应用，2003(11):13－15.

［16］ 杨保华.航天器制导、导航与控制［M］.北京:中国科学技术出版社，2011.