内聚度和粒度在作战任务分解评估中的应用

董 涛， 刘付显， 李 响

(空军工程大学防空反导学院，西安 710051)

0 引言

战术弹道导弹(Tactical Ballistic Missile，TBM)具有大跨度、高空高速、小RCS等特性，导致末段探测和拦截TBM的时间窗口仅为100 s左右。反导任务规划(Anti TBM Mission Planning，ATMP)必须以自主方式为主，快速统筹多种作战资源，严格按照高、精、准的时空要求规划整个作战任务执行过程［1－3］。任务分解是ATMP的基础和前提，目标是分解出高内聚、低耦合的任务序列，为ATMP后续任务(如任务调度、冲突消解等)的顺利执行奠定基础。

现有的任务分解方法过度依赖经验，分解结果带有较大的随机性和主观性，缺乏客观、快速、有效的方法来准确评估任务分解方案的优劣程度。针对此问题，引入内聚系数和粒度［4］的概念，提出基于内聚度和粒度的作战任务分解评估策略，以提高任务分解的柔性和可控性。

1 任务集的内聚度分析

内聚度是任务集内部各子任务关联紧密程度的量化值［5］，可作为任务分解的度量依据。任务集的内聚度越大，耦合性越弱，任务复杂性越低。分解作战任务时，首先聚类为模块化的任务集，再分解为内聚度更强的子任务集，再逐步分解为可直接执行的元任务序列。

1.1 任务关联矩阵

反TBM作战任务包含预警探测、目标截获、跟踪识别、火力拦截、杀伤效果评估等任务。任务之间因资源、时间、空间、时序等存在信息关联，构造任务关联矩阵(Task Associated Matrix，TAM)描述任务之间的关联［6］。TAM是一个N×N阶方阵，N代表任务的数目，矩阵的行和列分别对应不同的任务。矩阵对角线元素代表任务本身，令 rii=0，其他元素用 rij(i≠j，i，j=1，2，…，N)表示。所有任务之间的输入输出关系，如式(1)和式(2)所示。

式中:N为任务数量;rij为任务Ti与Tj之间的关系值，

1.2 任务集内聚系数

任务集内聚系数是任务集内聚度的量化值，等于任务关联系数和任务重用系数的乘积。任务关联系数α度量任务之间的关联程度，等于任务集内部所有任务对任务集的影响程度之和与任务集最大关联程度的比值。任务重用系数β是被重用的任务数与所有任务数的比值，反映了重用任务占所有任务数的比例［7］。

对任务集内部任意一个任务Ti，它与其他任务Tj(j=1，2，…，N，j≠i)之间的连接数量越多，输入输出关系就越复杂。输入连接只影响Ti本身，而输出连接则会对Tj产生直接的影响。各任务的任务关联系数αi如式(3)～式(5)所示。

式中:αi为Ti对Tj的影响程度;ki为Ti对Tj的影响系数;mi为Ti输出连接的数量。

将式(4)、式(5)代入式(3)可得

任务集最大影响程度αmax是指当任务集中的任务之间两两连接、互为输出时，所有任务对任务集的影响程度之和，如式(7)所示。

所有任务对任务集的影响程度之和与任务集最大影响程度的比值为任务关联系数α，表达式为

任务Ti对其他任务Tj产生影响，必须具备输出连接。具备输出连接的任务，都会被多个其他任务引用。任务集重用系数β为

任务集内聚系数λ是关联系数α和重用系数β的乘积。内聚系数λ为

如果初始任务集的λ高于分解后任务集的λ，说明初始任务集是紧内聚。若分解后的λ变小，则该任务集的内聚度不强，属于松约束，任务集可以继续分解细化，以提高完成任务的效率。

2 任务粒度规划

任务集具有层次性和相对性［8－9］。任务粒度既体现了某一任务集的层次结构，也反映了整体任务的规模和数量。任务粒度可作为评价任务分解的重要依据。任务粒度规划的目标是选择适宜的任务粒度，以降低任务复杂度。

任务粒度与任务数量成反比例关系:任务粒度越大，任务数量越小;任务粒度越小，任务数量越大［6］。任务粒度与任务数量的关系可描述为

式中:ξ为任务粒度;K为任务粒度系数。

如果任务粒度太大，则减弱任务的并行性和独立性。如果任务粒度太小，则增加执行时间和资源消耗。任务粒度必须综合考虑互相影响的任务数量和任务内聚度等因素。任务集的内聚度越大，其任务的粒度越小。即任务粒度ξ与任务内聚度λ成反比关系［10－12］，表达式为

式中，ω为常系数。

任务粒度太粗太大，将会减弱任务的灵活性，从而影响后续任务的执行;任务粒度过细过小，使得任务数量和任务间冲突增多，任务结构更加复杂。因此，合理规划任务粒度可增强任务之间的协同作用和内聚性，提高任务执行效率。

如果初始任务集粒度高于分解后的子任务集粒度均值，说明初始任务集的粒度过大，可以将初始任务集分解至合适粒度。如果初始任务集粒度低于分解后的子任务集粒度均值，说明初始任务集粒度合适，可保持初始任务集。

3 实例分析

当有5个TBM来袭时，拦截这5个TBM可视作5个作战任务。不同作战任务之间存在着时间、资源、空间等多种约束关系，将其抽象概括，可得到初始任务集T0，如图1所示。数字代表任务的编号，箭头代表任务之间的输入输出方向［7］。

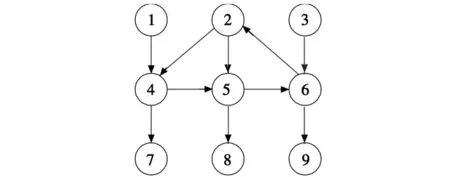
图1 初始任务集T0Fig.1 Initial task set

分解方案有两种，方案一将初始任务集T0分解为3个子任务集T1、T2和T3，如图2所示。方案二将初始任务集T0分解为2个子任务集T1和T2，如图3所示。

图2 任务分解方案一Fig.2 Task decomposition scheme 1

图3 任务分解方案二Fig.3 Task decomposition scheme 2

根据式(1)、式(2)得T0、方案一、方案二的任务关联矩阵，分别如式(13)～式(15)所示。根据式(8)、式(9)和式(12)计算任务关联系数、 重用系数和任务粒度，计算结果如表1所示。

表1 任务分解方案分析Table 1 Task decomposition scheme analysis

方案一分解后的子任务集T2的内聚度较高，但是T1和T3的内聚度偏小，粒度均值大于T0的粒度，T0不能按照方案一分解。方案二的T1和T2内聚度高，且粒度均值小于T0的粒度，T0可按照方案二细化分解。但是T1和T2的粒度相差10倍以上，方案二需进一步优化。另外，粒度是一个相对的概念，其大小和分解方案必须综合考虑任务复杂程度、规模大小、指控结构等因素。

4 结语

针对现有任务分解缺乏客观、全面的评估方法，本文提出基于内聚度和粒度的方法定量评估任务分解方案。通过分析影响内聚度的主要因素，建立基于任务关联矩阵的量化模型，评估不同粒度层次下的任务分解结果。本文仅考虑了任务之间的串行和并行关系，下一步将对耦合任务进行研究，并实现任务分解结果的自适应性控制，完善任务分解方案。

［1］ 祝江汉，黄维，李建军，等.面向新任务插入的电子侦察卫星任务规划方法［J］.火力与指挥控制，2011，36(7):174－177.

［2］ 刘书雷，刘长利，沈雪石.美国导弹防御系统发展动向及对策思考［J］.现代防御技术，2011，39(3):1－3.

［3］ 杨萍，毕义明，肖海波，等.复杂约束下的导弹作战任务规划模型和算法研究［J］.指挥控制与仿真，2009，31(2):14－17.

［4］ 郁湧，唐家华，李文宏，等.一种基于结构熵的类内聚度度量方法［J］.系统工程与电子技术，2009，31(3):702－704.

［5］ 罗爱民.信息系统体系结构设计中系统内聚度分析方法［J］.国防科技大学学报，2010，32(5):118－122.

［6］ 何玉安.基于本体的制造网格任务管理关键技术研究［D］.上海:上海大学，2008.

［7］ 邱福生.型号产品工艺分工系统及其关键技术研究［D］.哈尔滨:哈尔滨工业大学，2007.

［8］ 郝京辉，孙树栋，吴秀丽，等.网络化协作环境下机械产品加工任务粒度分析［J］.计算机集成制造系统，2006，12(3):451－457.

［9］ 修保新，刘振亚，张维明，等.基于粒度计算的指控系统效能测度的探索性建模方法［J］.国防科技大学学报，2010，32(5):123－128.

［10］ ENDER T，LEURCK R，WEAVER B.Systems－of－systems analysis of ballistic missile defense architecture effectiveness through surrogate modeling and simulation［J］.IEEE Systems Journal，2010，4(2):156－166.

［11］ 庞辉，方宗德.网络化协作任务分解策略与粒度设计［J］.计算机集成制造系统，2008，14(3):425－430.

［12］ 王国胤，张清华，马希骜，等.知识不确定性问题的粒计算模型［J］.软件学报，2011，22(4):676－694.