用混合蛙跳算法的智能防空火力分配
2012-08-27韩占朋王玉惠姜长生吴庆宪
韩占朋, 王玉惠, 姜长生, 吴庆宪
(南京航空航天大学自动化学院,南京 210016)
0 引言
在防空作战中,由于空袭目标数量众多,威胁等级各异,飞行诸元繁杂,己方防空武器种类、数量众多,作战范围多变,火力优化历来都是其难点之一。因此,开展防空火力分配问题的研究是十分必要且具有实际意义的。火力分配是一个离散的、带约束的组合优化问题,属N-P问题[1]。近十几年来,智能算法的出现及蓬勃发展为解决这一问题提供了更强有力的工具,如人工免疫算法[2]、基于遗传的人工鱼群算法[3]、改进的粒子群算法[4]、禁忌搜索与粒子群算法的混合优化策略算法[5]、蚁群算法[6]等都比较好地解决了火力优化问题,但同时也有各自不足之处。本文引入一种新的智能计算方法——混合蛙跳算法,该算法具有概念简单、参数少、计算速度快、全局搜索能力强、易于实现的优点[7]。根据算法原理,通过特殊的编码方式更新青蛙位置,加入了一个变区间步长σ,逐步得到全局最优方案。
1 火力分配建模
假设我方有m组不同的防空武器,每组防空武器的数量为vk,k=1,2,…,m。预警系统发现有n批不同目标,数量为 qk,k=1,2,…,n。n 批目标的威胁系数用 wj表示,j=1,2,…,n。
为使分配的火力单元能有效打击目标,首先定义防空武器的火力单元条件约束总矩阵R。在武器系统的有效作用区域和组间最大转火时间内,同组内的武器单元由于作用区域差异及敌机飞临特征,能有效打击的目标各不相同。因此建立防空武器单元对n批目标开火的约束矩阵为

式中:Rmn表示第m组防空武器的第n个火力单元的目标分配约束阵。rij表示该火力单元对第i批目标的第j个目标的条件约束,属二值变量,由该火力单元的作用区域、弹药装载量、转火时间、武器的自身属性及目标特点决定。
注1 单独考虑武器及目标类型因素时,烟幕弹对F-16战斗机基本没有作用,则rij=0,但对AGM-137 TSSAM 巡航导弹的毁伤可达到 0.804[8],rij=1。rij=1时表示可以分配,否则为零,不可分配。
假定同批内目标的类型及威胁系数相同,防空武器打击相同类型目标的毁伤概率相同,只需确定武器系统分配给每批目标的数量即可得到火力决策阵。则毁伤矩阵P与火力决策矩阵X分别为

pij表示第i组防空武器对第j批目标分配一个火力单元后对目标的毁伤概率;xij表示第i组防空武器对第j批目标分配的火力单元数。
为了最大限度地杀伤空袭目标,将总的防空火力单元的杀伤概率作为目标函数,使杀伤达到概率最大值。即

上述模型能够真实地模拟打击情况,在全局分配的同时兼顾单个火力的状态,与以往模型相比,提高了分配精度,可确定各组武器的每个单元的作战对象。当面临多批空中目标威胁时能最大限度地利用防空武器资源。下面根据模型,给出火力决策阵的关联解阵。
为了直观简便,本文采用十进制编码方式,每个解依照火力单元号排列,m组防空武器构成一个m维解矩阵。解值表示火力单元所分配到的目标。在满足矩阵R的前提下,关联解阵为
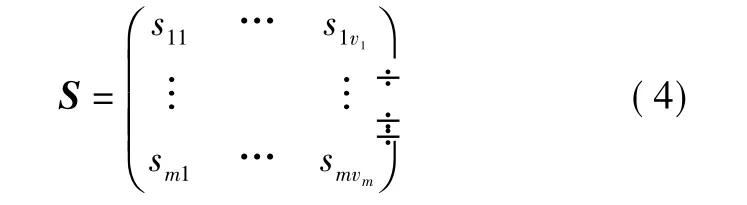
其中,s11代表第1组防空武器的第1个火力单元分配的目标。由解阵S可得到火力决策矩阵X,依照式(3)可计算解阵S的代表的适应值。

2 混合蛙跳算法
2.1 混合蛙跳算法
混合蛙跳算法(Shuffled Frog Leaping Algorithm,SFLA)是2001年 Muzaffar Eusuff和 Kevin Lansey为了解决水管网设计提出的一种基于青蛙觅食的群体智能搜索算法[9]。现已经证明该算法满足随机搜索的全局收敛条件,能够保证做到全局收敛[10]。
SFLA的原理是随机得到k只青蛙构成初始种群,第 k 只青蛙用 Fk=(fk1,fk2,…,fks)表示,其中,s表示解的维数。之后,将种群内的青蛙按照适应度降序排列并划分成l个模因组,每个组代表一个子群,内含有h个个体。在进化过程中,第1个解放入第1个子群,次第放入,直到第l个解放入第l个子群。然后,将第l+1个解再次放入到第1个子群,第l+2个解放入到第2个子群,循环分配,直到所有的解分配完毕。对每个子群而言,适应值最大的青蛙用Fb表示,适应值最小的青蛙用Fw表示,而整个种群中适应值最大的青蛙用Fg表示。之后对每个子群进行局部最优搜索并更新Fw。经过更新后,如果得到的青蛙Fw优于原来的青蛙Fw,则取代原来子群中的青蛙;否则,用Fg取代Fb,重新更新,如果仍然没有改进,则随机产生一个新蛙取代原来的Fw。重复上述操作。当完成局部搜索后,将所有的青蛙重新混合排序并划分子群,再次进行局部搜索,如此反复直到满足终止条件。
算法的框架是一致的,关键是青蛙的更新。为了使蛙跳算法适用于离散的火力分配问题,需改进其更新方式。下面介绍具体的改进方法:首先计算Fb与Fw(这里指最优、最差解阵S)的差异位置及其个数tmax(由Fb-Fw的值确定),随机得到相异的t个位置(t为随机数),用Fb相应位置上的数值更新Fw的相应位置。更新如下
首先在施工之前,项目部进行了实地考察和对当地建筑市场进行了解,并详细研究招标文件对该幕墙工程的描述要求,制定了幕墙深化规划设计的策划方案,需要注意的:①在方案中明确规定了幕墙深化设计的标准和要求。②结合实地,分别对两栋塔楼幕墙进行深化设计。③要求精确到每个螺丝钉的尺寸以及操作手法。④在绘制深化设计方案后,应当设置严格的会审流程,确定最终版本,积极向DEWAN监理公司工程师进行图纸报批、沟通,减少深化设计的时间周期。⑤在施工过程中,要严格监督分包单位按照深化设计的施工图纸以及各项专业的设计图纸中规定尺寸和要求的来进行操作,保证施工质量。

式中:Rre表示首先计算Fb与Fw的差值矩阵,其解表征了两者之间的差异,记录非零元素所在位置;L表示两者之间的差异位置集合。随机抽取,得到差异位置,进行相应位置的更新。受杂草算法[12]的启发引入一个可变步长σ来控制变异的个数t。
如果用 σinit,σfinal,σcur,imax,i以及 n 分别表示初始区间步长、最终步长、当前步长、最大迭代次数、当前迭代次数及非线性调节指数,则它们之间的关系为

然后根据N(0,σ2)随机产生一个扩散值,即t(t<tmax)的解。应用式(6)确保了算法在迭代过程中,t以非线性的方式逐渐减小,相当于遗传算法中的交叉过程向变异过程转变。在整个迭代过程中,从多点变异方式向单点变异方式转变,最终在最优解的小范围内摆动,试图寻找全局最优解,因而整个寻优过程具有更强的鲁棒性。
2.2 蛙跳算法分配火力
蛙跳算法步骤如下所述。
1)编码初始化青蛙种群k=100。
2)按式(1)计算每只青蛙的适应度,并按降序排序。搜索出全局最优可行解Fg、各个子群中的最优可行解Fb和最差可行解Fw。
3)将种群划分成10组,每组10个个体,子群进化,并按式(5)、式(6)更新最差可行解Fw得新解Fq。
4)如果 Fq优于 Fw,则令 Fw=Fq;否则,令 Fg取代Fb产生新的可行解F'q,如果F'q优于Fw,令Fw=F'w;否则随即产生新解Fw。重复步骤3),直到子群的最大迭代次数imax=5。
5)将所有的青蛙重新混合排序,重复步骤3)~5)。
6)达到种群的最大迭代次数Imax=20或精度要求停止,输出Fg。
3 实例仿真
依据上述模型,用改进的SFLA算法进行仿真。仿真环境为:P4 2.4 G/512 M微机,Windows操作系统,VC++6.0开发平台。假定发现7批目标将在相邻时刻到达,其间隔小于我方武器转火间隔,假定每批目标数量都为5个(其数量对仿真无影响)。我方防空武器有6组,每组的火力单元数量分别为 8、6、7、6、5、8 个。火力单元对目标的杀伤概率及目标威胁如表1所示。

表1 火力单位对目标的杀伤概率Table 1 Kill probability of fire unit to target
依照2.2节中的蛙跳算法步骤及参数,仿真运行,得到最优解为

目标适应度函数值为23.5。
为对算法进行纵向比较,设定子群迭代5次,分别就整个种群迭代 20、50、100、200、500 次仿真,分别随机运行50次取均值,结果如表2所示。
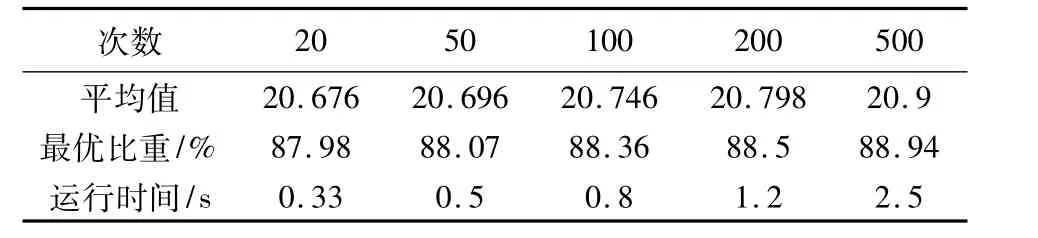
表2 结果比较Table 2 Comparison of the simulation result
上述结果表明,当迭代20次时,结果均值已经到达最优值23.5的87.98%,同500次仿真结果均值相差0.224,差异很小。由此说明蛙跳算法能快速收敛。
为了对仿真结果进行横向比较,同时采用遗传算法及其改进算法对该战例进行了计算(群体大小100、交叉率0.6、变异率0.01,迭代次数50次),由其50次独立实验的结果得到的目标函数值及时间均值与蛙跳算法比较如表3所示。

表3 毁伤比较Table 3 Comparison of kill probability
由上表可以看出,利用蛙跳算法进行火力分配在缩短运行时间的同时可以得到较好的效果,此外,当结果趋于稳定时,GA、IGA迭代次数明显高于SFLA,也间接证明了SFLA能快速收敛。究其原因在于族群中的局部模因进化与族群间的混合交流交替进行,使群体信息更加丰富的同时也大大提高了算法的收敛速度,此外,可变步长σ使得解总是稳定在最优附近,防止算法在最终阶段出现下滑现象,该结果也证明了模型的正确性。
4 结束语
火力分配历来都是提高防空效率,打击目标保证己方生存能力的关键环节。本文就混合蛙跳算法在解决防空作战中火力分配问题的应用进行了初步探索。通过一个可变步长因子σ使整个过程具有更强的鲁棒性。应用实例仿真得到理想的结果,通过横向与纵向比较,证实了蛙跳算法具有很快的收敛速度及较高的精度。同时也表明了模型的正确性,为防空火力分配优化提供了一种新的有效方案。
[1] 阮旻智,李庆民,刘天华.编队防空火力分配建模及其优化方法研究[J].兵工学报,2010,31(11):1525-1529.
[2] 赵振锋,吴庆宪,姜长生.基于遗传的人工鱼群优化之武装直升机对地攻击火力分配决策[J].电光与控制,2011,18(3):31-33.
[3] 丁铸,马大为,张学锋,等.基于改进微粒群算法的火力分配[J].弹箭与制导学报,2006,26(1):575-580.
[4] 丁铸,马大为,于存贵,等.基于禁忌搜索与微粒群优化算法的混合优化策略算法在目标分配问题上的应用[J].兵工学报,2007,28(9):1127-1131.
[5] 严建钢,郑保华,黄晅,等.防空火力分配问题的蚂蚁算法模型[J].火力与指挥控制,2008,33(8):91-93.
[6] 李英海,周建中,杨俊杰,等.一种基于阈值选择策略的改进的混合蛙跳算法[J].计算机工程与应用,2007,43(35):19-21.
[7] 赵玲.防御阵地智能火控及指挥决策系统研究[D].南京:南京航天航空大学,2010:36-38.
[8] EUSUFF M M,LANSEY K E.Water distribution network design using the shuffled frog leaping algorithm[C]//World Water Congress,2001:1-8.
[9] 骆剑平,李霞,陈泯融.混合蛙跳算法的Markov模型及其收敛性分析[J].电子学报,2010,38(12):2875-2880.
[10] MEHRABIAN A R,LUCAS C.A novel numerical optimization algorithm inspired from weed colonization[J].Ecological Informatics,2006,1:355-366.
