运用特殊化与一般化探究一道高考题

☉江苏省东台市安丰中学 金小进

一、探究的起因

（1）略.

（2）若|OG|2=|OD|·|OE|，①求证：直线l过定点；②略.

简析：不难计算，不论斜率k为何值，直线l恒过定点（-1，0），现改变直线x=-3或椭圆方程，直线l是否还过定点？如果是，所过定点与直线x=-3和椭圆方程有何关联？带着这个疑问，我们进行以下探索.

二、特殊化归纳

题中要求直线l的斜率k＞0，事实上，如果把该条件放宽，考虑特殊情况：直线l垂直于x轴.这即定点，正好也符合原题的结论.如果椭圆方程为=1，直线方程为x=m，那么D（m，0），G（a，0），E），又考虑到直线方程x=m与点E）的内在联系，于是把直线方程处理为，则其对应点E（m，0），这样就对应着椭圆a=1的“类准线”与“类焦点”的问题，于是我们大胆猜想：

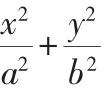
三、一般化探索

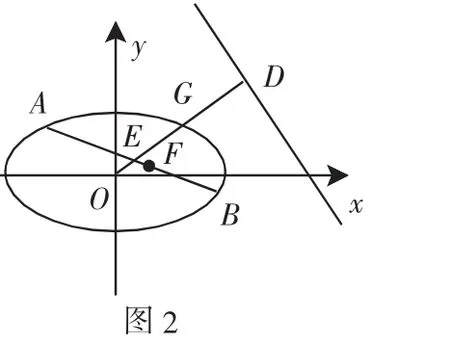
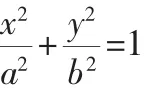
证明：设E（p，q），

①充分性：因直线l过F（m，n），

故q=n.

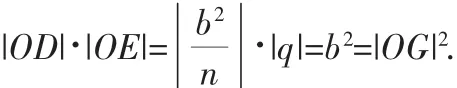
②必要性：由|OG|2=|OD|·|OE|，

故q=±n.

因OE为 射线，所以yE与yD的符号相同.

q与n同号，q=n，所以直线l过F（m，n）.

另设A（x1，y1），B（x2，y2），

①充分性：因直线l过点F（m，n），

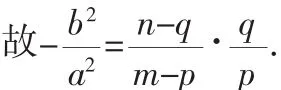
又因E、G、D三点共线，所以|OD|·|OE|=|OG|2.

由OE为射线可知xD与xE同号，

故直线l过极点F.

至此，运用特殊化的手段，发现了高考题的背景：类准线与类焦点；通过一般化的手段得到更深层次的背景：极线与极点.进一步地，还可以推广到双曲线与抛物线中去.

结论4 抛物线C：y2=2px，极点F（m，n）对应着极线：nyp（x+m）=0，不过原点的直线l交抛物线C与A、B两点，弦AB的中点为E，射线OE交抛物线C于G点，交极线ny－p（x+m）=0于D点，则|OG|2=|OD|·|OE|的充要条件是直线l过极点F.

四、再特殊化分析

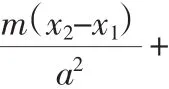
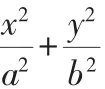
结论7 抛物线C：y2=2px，其极点F（m，n）对应着的极线l1：ny－p（x+m）=0，不过原点的直线l交抛物线C与A、B两点，弦AB的中点为极点F，射线OF交抛物线C于G点，点G处的切线为l2，则l∥l1∥l2.

我国著名数学家华罗庚教授曾说，复杂的问题要善于“退”，足够地“退”，“退”到最原始而又不失重要性的地方，是学习好数学的一个诀窍.运用特殊化找出结论成立的简单情形正是华先生所讲的“退”，由此获得的启示又将为探究问题的一般性提供某种对比，从而就有可能运用一般化的手段发现问题的背景，揭示问题的本质.