在习题的变式教学过程中优化学生思维品质

☉江苏无锡市山明中学 王 颖

在习题的变式教学过程中优化学生思维品质

☉江苏无锡市山明中学 王 颖

习题课出现的最常见的问题是学生收获小，并且讲过的题目稍加变化再次出现学生依然会错.很多时候我们可能会气急败坏的责怪学生：“怎么这么笨呢！讲了还错！”可是我们有没有反思教师自身的原因呢？为什么稍稍变化学生就不会做了呢？我们有没有教会学生应对变化的能力？如果我们能在平时的习题教学中，就能够从多个角度进行变换，常此以往，我想学生肯定能够形成应对变化的能力，从而达到“任尔东南西北风”，我亦游刃有余的境界.

下面是我在习题教学的过程中的几例尝试.

一、在习题的变式教学过程中，训练学生的迁移能力.

习题（华师版实验手册）：

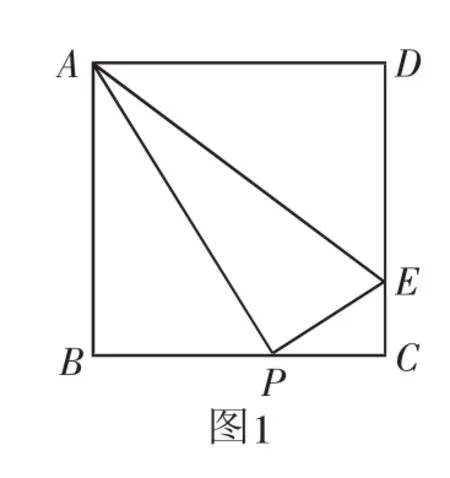
分析：本题是一道与相似三角形有关的问题，图形特征明显，由于没有指明对应关系，故分两种情况：△ABP∽△PCE、△ABP∽△ECP.

以原图为原型，从不同角度出发，二次函数的最值问题也经常与相似相结合.

变式一：正方形ABCD边长为4，P、E分别是BC、CD上两个动点，且AP⊥PE.

①证明Rt△ABP∽Rt△PCE.

②设BP=x，梯形ABCE的面积为y，求y与x之间的函数关系式，当P运动到什么位置时，四边形ABCE面积最大，并求出最大面积.

③当P运动到什么位置时，Rt△ABP∽Rt△APE，求x的值.

分析：本题是原习题的特殊情况，第②问直接用①的结论把EC用x表示出来，建立二次函数，配方法求最值，第③问是第①的逆向问题，对学生迁移能力有很好培养.

简解：①略.

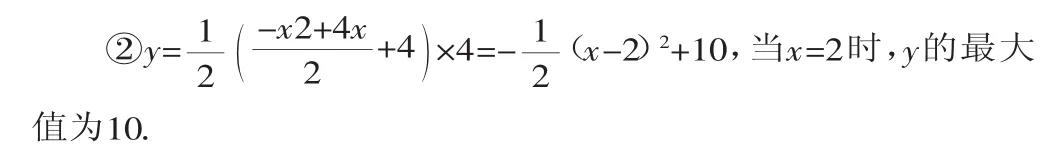
③当P运动到BC中点时，Rt△ABP∽Rt△APE，x=2.

变式二：

（2010南通中考题）如图2，在矩形ABCD中，AB=m（m是大于0的常数），BC=8，E为线段BC上的动点（不与B、C重合），连接DE，作EF⊥DE，EF与射线BA交于点F，设CE=x，BF=y.

（1）求y关于x的函数关系式.

（2）若m=8，求x为何值时，y有最大值，最大值是多少？

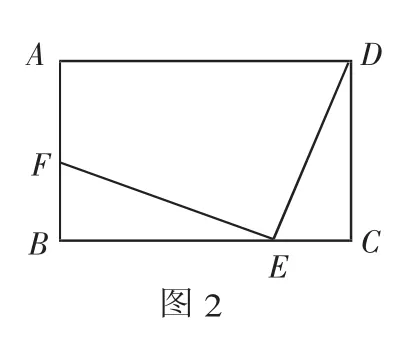
分析：本题又把正方形变成矩形，如何将正方形中的结论和思考方式迁移到矩形中去，获得对原题更深入的认识，学生在逐步深入的变式习题中会得心应手很多.

通过对这个习题的变式处理，我想学生可以增强这样的几种迁移能力：从简单题型迁移到复杂的综合题型；从图形的形似迁移到题目的相似；从题目相似迁移到题目相异.同时在迁移的过程中，注意辨证思考问题，迁移不是无边界的，如果脱离了最初的原型，迁移可能就会造就错误.

二、在习题的变式教学过程中，训练学生的发散能力

发散思维是要求解决问题的斯文朝多种可能的方向扩散，不拘泥于一个途径，一种方法，代数与几何相融，思路宽阔的多种变通方法.

解法一：利用前后两项依次通分，加至最后一项，这种方法虽能求出，但对出现字母的情况不适用.

解法二：仔细观察各项的特征，第一项是第二项的2倍，可设

两项乘以2或除以2都可以解决问题.

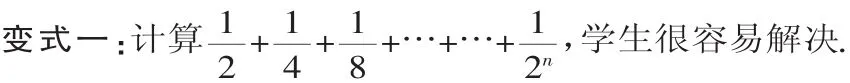
变式二：如果幂中底数变化，你还认识吗？

在这个题目的变式处理中，我希望学生学会从不同的角度去进行发散，从而在实际的生活中学会运用多种方案来解决问题.

三、在习题的变式教学过程中，训练学生多角度思考同一问题的能力

在教学中，我们经常会遇到这样问题：同一个问题讲过多遍，学生仍然会错.为什么？我想大概每次讲都是同一个角度，学生对这个问题的认识始终是片面的.只有从不同角度审视同一个问题，才能形成整体感，让学生彻底理解.

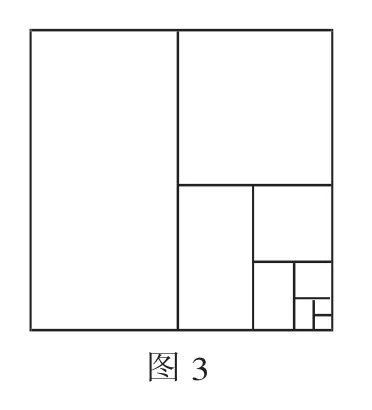
例如：一慢车和一快车沿相同路线从A到B地，所走路程与时间的函数图像，如图4.

（1） 慢车比快车早出发__________小时，快车追上慢车时行驶了__________千米，快车比慢车早__________小时到达B地.

（2）在下列问题中任选一题求解.

①快车追上慢车需几个小时.

②求慢车、快车的速度.

③求A、B两地路程.

角度1：看成函数题.

读出需要的点的坐标，分别设y1=k1x过（18，a），y2=k2x+b过（2，0），（14，a），且交点纵坐标为276，求出y1=46x（0≤x≤18），y2=69x-138（2≤x≤14），以及a、交点坐标.有了这些信息，（2）中任一小题都迎刃而解.

角度2：看成应用题.

慢车出发2小时后快车出发，且快车比慢车提前4小时到达，设快车速度为xkm/h，慢车速度为y km/h.

角度3：看成“A”字型相似.

诗云：“横看成岭侧成峰，远近高低各不同”.

在这个题目的变式处理中，我希望学生能够学会从多个角度来审视同一事物，从而抓住其本质，真正体会到什么叫“万变不离其宗”，而不是一转身熟悉的面孔变成了陌生的背影.

习题的变式处理，有很多方法：变陌生为熟悉，变具体为抽象……变式处理有利于将学生从题海中解放出来，有利于发展和优化学生的思维品质，使之更好地持久发展.知识一方面是生活的需要，更重要的是作为培养能力的载体，我们要更好地体现后者.