非线性电阻电路分段线性分解拟合及仿真

2012-08-23葛年明马鑫金龚秋英

电气电子教学学报 2012年1期

葛年明，马鑫金，龚秋英

(三江学院电工电子实验中心，江苏南京 210012)

0 引言

在电路分析中，线性电阻元件的伏安特性可由欧姆定律u=Ri表示，在u-i平面是通过原点的一条直线。非线性电阻元件的伏安特性不满足欧姆定律而遵循某种特定的非线性函数关系。由线性电阻元件构成的电路，称为线性电阻电路，否则称为非线性电阻电路［1］。由于非线性电阻本身的特殊性，因而分析研究非线性电阻具有重要意义。

非线性电阻可用一个函数关系式来表征，或可用一条图解曲线的方法表示。在图解法中，某些非线性电阻的伏安特性曲线可以分段线性化，对每段线性区域都可以用线性电路的计算方法分析。而分析非线性电阻电路的基本依据仍然是基尔霍夫定律和元件的伏安特性［2］。

1 非线性电阻元件的伏安特性

(1)常见电路元件的伏安特性

对于一个二端元件，不论内部组成，其端口电压与电流的关系可以用u-i平面的一条直线或曲线表示。常见的二端电阻元件有二极管、稳压管、恒流管、电压源、电流源和线性电阻。伏安特性如图1所示。运用这些元件串、并联或混联就可得到各种单向单调的非线性伏安特性曲线，故用分段线性化的方法即可拟合得到非线性二端电阻的电路。

图1 常见的二端电阻元件及伏安特性

(2)凹电阻［3］

当两个或两个以上元件串联时，电路的伏安特性图上的电压是各元件电压之和。如图2(a)所示，是将图1中的(a)、(e)、(f)三个元件串联组成，其伏安特性曲线如图2(b)所示。它是由(a)、(e)、(f)三个元件的伏安特性在i相等情况下的相加而成。具有上述伏安特性的电阻，称为凹电阻，电路图符号如图2(c)。

图2 凹电阻组成及伏安特性曲线和电路图形符号

可见凹电阻的主要参数是电压源US和电导G(G=1/R)，改变US和G的值，就可以得到不同参数的凹电阻。需要指出的是凹电阻中的元件电压源US可以等于0，电导G可以为无穷大(R=0)，但不能同时如此设定。

(3)凸电阻［3］

与凹电阻相对应，凸电阻则是当两个或以上元件并联时，电路伏安特性图上的电流是各元件电流之和。如图3(a)所示，是将图1中的(b)、(e)、(f)三个元件并联组成，其伏安特性曲线如图3(b)所示。它是由(b)、(e)、(f)三个元件的伏安特性在U相等情况下的相加而成。具有上述伏安特性的电阻，称为凸电阻，电路符号如图3(c)。

上述电阻的主要参数是iS和R=1/G，改变IS和R的值，就可以得到不同参数的凸电阻。需要指出的是凹电阻中的元件电流源iS可以等于0，电导G可以为0(R=∞)，但不能同时如此设定。

2 分段线性的非线性电阻分解和拟合

图3 凸电阻组成及伏安特性曲线和电路图形符号

分段线性化法是将非线性电阻的伏安特性曲线近似地用分段直线来表示。在分段线性的非线性电阻中，对于给出的各种单调函数关系式可用图解曲线的方法进行拟合。以凹电阻和凸电阻作基本积木块，运用串联分解法或并联分解法进行分解拟合，得出各种所需的非线性电阻。

(1)串联分解拟合法

串联分解拟合法在伏安特性图中是在同一电流i下，电压相加得到总电压。可将整条非线性电阻伏安特性曲线分解成若干条直线段的凸电阻串联。

如要求综合图4(a)的伏安曲线，则可将曲线分解成如图4(b)和(c)所示的2条直线段。图4(b)直线段是电流源IS=0及斜率为R=0.5KΩ的凸电阻;图4(c)直线段是电流源IS=2mA及电阻R=∞的凸电阻。可见是两个凸电阻串联如图5(a)所示，最后组成的电路图如5(b)。

图4 伏安特性

图5 串联分解拟合法

(2)并联分解拟合法

并联分解法在伏安特性图中是在同一电压u下，电流相加等得到总电流。可将整条非线性电阻伏安特性曲线分解成若干条直线段的凸电阻并联。

如要求综合图6(a)的伏安曲线，则可先将第一象限中曲线如图6(b)的2条直线段用二个凸电阻并联，电路如图6(c)并简化成6(d)。

图6(a)在第四象限中的曲线，则是第一象限中曲线以原点为中心的对称曲线，只需将电路6(d)反向，并再与电路6(d)并联，由电路6(e)即可得图6(a)的伏安曲线。

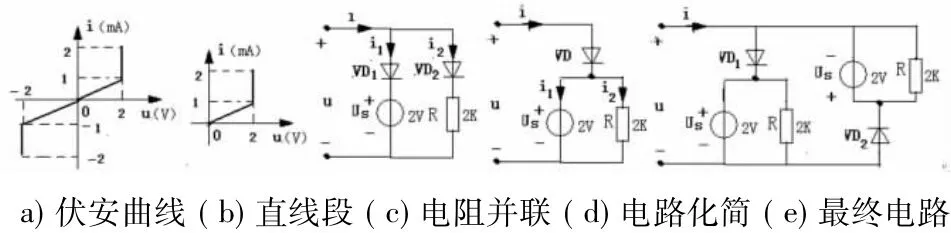
图6 并联分解拟合法

实际上，不少非线性电阻的伏安特性曲线是串联分解法和并联分解法混合运用拟合而成。也就是说，用串联分解法第一次分解出分图后，各分图特性的拟合可以用串联分解法或并联分解法拟合;同样，第一次用并联分解法分解出分图后，各分图特性的拟合可以用串联分解法或并联分解法拟合。

3 电路案例分解拟合及仿真

对于图7的非线性电阻电路伏安特性，以第一象限为例分析、拟合电路图并仿真与要求比对。

图7 伏安特性的非线性电阻电路

(1)电路的分解拟合

在ABC段上参考凹电阻基本模块，其斜率为0.5，可以用图8(a)电路实现;在CD段同样用凹电阻，只是斜率增加为1，即电阻R改为1kΩ，与8(a)电路并联，如图8(b);在DE段上斜率减小，电阻R改为1.667kΩ如图8(c)所示的。再用凸电阻电路串联(也可用一个凹电阻并联)，如图8(d)所示。

第三象限的图形与第一象限完全对称，可以将第一象限的电路反过来即可。

图8 非线性电阻电路第一象限电路的分解和拟合

(2)拟合电路的仿真

若要实现图7中的第三象限中的曲线，只需将电路8(d)中所有有极性元件反向，并再与电路8并联，就可完成图7要求的伏安特性曲线(图9)。

(3)仿真电路的数据和曲线

表1 仿真电路的数据

(4)仿真数据的误差分析

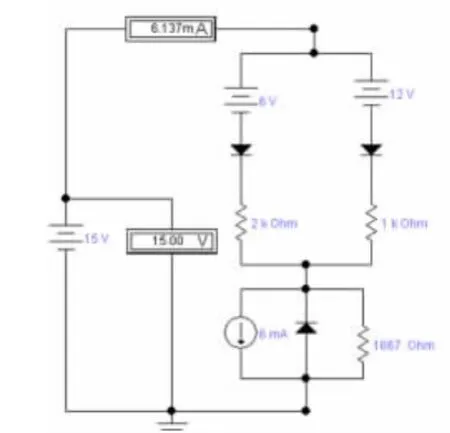
图9拟合电路仿真

图10仿真数据由Excel转化为曲线

从表1的仿真测量数据与所要求的曲线数据相比较，误差最大处是在电压20V时，相对误差达到1.7%，从两条Excel曲线也清楚地看到了这一现象(图10)。这是由于凹电阻和凸电阻的组成中，二极管是理想型的［3］，相当于工作在开路或短路状态下，而在仿真中的二极管是实际二极管，它本身也是非线性元件，造成了各点处的误差。由于目前为止，还没有生产出正向完全导通与反向完全截止的理想二极管，在实际使用中，选用正向压降小的锗管误差会比硅管要小。