案例教学法在高职数学教学中的应用

李建杰

案例教学法在高职数学教学中的应用

李建杰

北京电子科技职业学院 北京 100029

案例教学法是从实际问题出发，经过合理简捷的推导归纳，从而引出数学知识。采用案例教学法，不仅可以激发学生的学习兴趣，引导学生积极主动地参与学习过程，提高教学质量，而且有利于提高学生解决问题的能力，提升数学素养。

高职数学；案例教学；教学实践

10.3969/j.issn.1671-489X.2012.36.107

作者：李建杰，副教授，研究方向为数学教育。

Author’s addressBeijing Polytechnic, Beijing, China 100029

1 问题的提出

高等数学作为高职院校一门重要的基础理论课程，它所提供的思想方法、理论知识不仅是学生学习专业课程的重要工具，也是培养学生创新能力的有力支撑，并为学生的终身学习奠定基础。依据高职教育的人才培养目标，数学课程的教学必须以强化知识应用为导向，以培养学生的应用能力为目标，突出数学知识与实际应用、相关专业内容的契合。

近年来，随着高职院校的扩招，学生的数学基础较之过去有所下降，且水平参差不齐，导致高等数学的教学目标很难实现。怎样做才能实现教学中既能准确地讲授概念及公式的推导等知识，又能提高学生的学习兴趣，使学生比较容易地掌握并运用它们解决问题？著名教学论专家孔德拉秋克曾经说过，教学的成败在很大程度上取决于教师能否妥善地选择教学方法。因此，在高等数学的教学中，教师如何运用适当、科学的教学方法，就成为提高教学效果的基础与条件。

在总结教学经验的基础上，受到案例教学法的启发，笔者发现：在讲授数学概念及一些公式的推导时，如果能充分采用直观的案例教学，可使概念的讲解言简意赅、公式的推导深入浅出，有利于激发学生学习的积极性和探索精神，启迪学生的思维，拓宽学生的视野，帮助他们系统地理解并掌握相应的数学知识和思维方法。

2 案例教学法在高等数学教学中的优势

案例教学法主要是教师围绕特定的教学、培训目的，把实际中真实的情景加以典型化处理，形成供学生思考分析和决断的案例，通过独立研究和相互讨论的方式，来提高学生分析问题和解决问题的能力。教师引导学生探究的过程就成为讲授数学基础知识的过程，二者融为一体。

与传统的教学方法相比，案例教学法具备5个优势：

1）案例教学法可以把抽象概念置于一定的情景之中，使学生清楚地认识到所要学的概念在实际生活、专业课中的用处与表现形式；

2）案例教学法不仅仅是让学生简单地掌握理解概念，而且更注重培养学生的探究精神和解决问题的能力；

3）学生通过案例教学得到的知识不是外界强加给的，而是内化了的知识；

4）案例教学能启发学生的思维，调动学生的学习兴趣，使艰涩的数学教授过程从“要我学”转变成为“我要学”；

5）案例教学法缩短了教学情景与实际问题情境的差距，有利于扭转学生普遍认为学数学只是纸上谈兵的错误思想。

3 案例教学法在高等数学教学中的可行性

从高等数学发展历程不难看出，高等数学是伴随着其他学科的发展而发展的，高等数学的诸多进展当初更是顺应其他学科发展对数学工具的需求应运而生的，因此它天生具有广泛的应用性。从这个角度看，高等数学除了“基础性”以外还具有“工具性”的一面，它是学生后续学习专业课程的工具。因此，培养学生应用数学的意识和能力已成为数学教学的重要方面。在案例教学的实施过程中，案例的选择与案例的使用是需要解决的核心问题。

3.1 案例的正确选择

要组织好案例教学，最基本的是选择好案例，选择案例时要充分考虑四方面的因素。

一是目的明确。教学中所用到的案例不仅要符合教学目标和教学内容的需要，而且要符合学生的认知水平，利于学生理解知识，并能够运用所学知识解决类似问题。

二是趣味性强。通过对本院学生的问卷调查显示，学生对由实际问题引入数学知识都怀有浓厚的兴趣，但普遍存在畏难情绪。针对这一特点，在收集案例时，选择那些既有趣味又能充分体现数学思想方法的简单案例，从培养兴趣着手，让学生逐步体会到解决问题的方法和数学的重要性。

三是具有代表性和广泛性。案例教学要尽量避免涉及过多的专业知识，同时要考虑到当今科学技术的发展、学科间的互相渗透。这些问题的实际背景容易被学生了解和接受，有的就是平时有所接触但又未深入了解的普通问题，学生产生浓厚兴趣，从而愿意去深入了解。

四是具有真实性。学习数学的目的在于培养学生解决实际、专业中的问题，因此，案例选择的真实性和实用性尤为重要。

3.2 案例教学法的正确运用

根据荷兰数学教育家弗来登塔尔的数学教育思想，数学教育应该从学生的数学现实出发，从生活的现实出发，通过提出问题、分析问题、探究讨论直至解决问题，经过概括提高，升华为数学概念、数学法则及数学思想。高等数学中的许多概念都有良好的物理背景或几何背景，教学时结合学生已有的数学知识和生活经验，充分利用这些资源，引导和启发学生去发现和探究，揭示其中所包含的由特殊到一般，由具体到抽象的辩证过程，从而使学生了解数学概念的来龙去脉，体验数学概念的形成过程，领悟其中蕴涵的数学思想。

例如，讲解定积分的概念时，笔者选择下面的案例组织教学。

1）提出问题。建造一座横截面如图1所示的拱桥，假设界面的拱顶为抛物线型，桥孔为一矩形上加一半径为r的圆弓。试计算砌此桥的截面墙需用砖的数量。

2）分析问题。这看起来是一个简单的初等几何问题。先计算出桥的横截面积，再除以砖的横截面积，就可以得到需要砖的数量。

桥的横截面积=抛物线AmF下的面积-矩形BCDE的面积-圆弓CnD的面积

这里，学生通过已有知识，能求出矩形BCDE的面积和圆弓CnD的面积，而抛物线下所围面积，如何解决？

图1

图2

图3

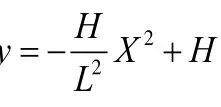
4）探究与讨论问题。

①教师先向学生呈现高等数学事例。德国天文学家开普勒发明了一种求圆面积的方法：把圆分割成无穷多小扇形，小扇形可近似用小的等腰三角形来代替。学生从中受到启示，即局部以直代曲以及化整为零、积零为整的思想。再要求学生求出图3所示曲边梯形的面积。学生想到用一些小矩形来近似求出它的面积，用4个小矩形的面积之和代替。于是，另一个学生说要想误差更小，分割的小矩形越多越好。

②恰当利用现代教学手段，将自我探索引向深入。演示随着矩形个数的增加，这些小矩形所组成的台阶型面积就越逼近抛物线下的面积的动画过程，使得在黑板上较难表现的函数极限过程得到较好的展示，使抽象的教学内容变得直观、生动、形象。

③引导学生分析、讨论。通过探究过程学生体验：分割的意义是化整为零；近似代替的目的曲转化为直；求和的作用是积零为整；求极限的目的是直转化为曲，获得精确数值。

④自主与合作学习，教师给予必要的指导。

下面请同学们一起计算面积A：

继续这种作法……

把区间[0,1]n等分，则台阶型面积：

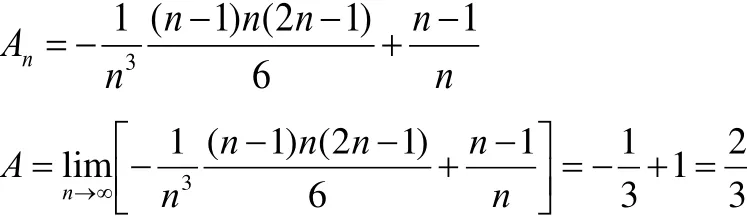
⑤引导学生归纳反思。曲边梯形的面积与给定区间、分割方法、取点的关系。求曲边梯形的面积体现了曲转化为直，直转化为曲，以及由此所反映出来的化整为零、积零为整的思想方法，是微积分乃至整个高等数学的一个重要方法。

通过实验对比，运用案例教学法的学生在此基础上举一反三，把解决单一问题得出的结论、方法和思路应用于解决更多的实际问题的能力明显强于对照班的学生。

案例教学法是在实际问题求解的铺垫下构建数学知识，不仅能使学生了解知识产生的背景，而且能够体验知识的探究过程，强化了对学生运用数学知识解决问题能力的培养，在实际教学实践中是切实可行的，值得重视和推广。

[1]云连英.微积分应用基础[M].北京:高等教育出版社,2006:92.

[2]席振伟.数学的思维方式[M].南京:江苏教育出版社,1995:6.

[3]富成华,崔殿军.高职高等数学“案例与实验”教学法初探[J].辽宁高职学报,2007(6):17-18.

Application of Case-based Method to Mathematical Teaching of High Vocational School

Li Jianjie

Case-based method is intended for solving problems in practice. Mathematical thinking can be used in the process of reasoning and concluding. By applying case teaching method, teachers can not only evoke students’ interest, encourage participation in the study, but can also help improve the students’ ability to analyze practical mathematical problems.

mathematics of high vocational school; case-based method; teac hing practice

G712

B

1671-489X(2012)36-0107-03