有限元方法对拱桥拱轴线优化的研究

瞿振华

(上海国康联同桥梁咨询有限公司，上海 200092)

1 概述

拱桥的拱轴线是设计的重要参数，直接影响到截面的内力分布和大小。在拱桥的实际设计过程中，对于悬链线拱拱轴的轴线系数的确定，通常采用“五点重合法”。但是由于压力线与拱轴线的偏离，在拱顶、拱脚都产生了偏离弯矩，实际上并不存在五点重合的关系。且通过少数几个点来逼近恒载压力线，也容易造成拱圈在荷载作用下某些截面下压力线与拱轴线偏差较大。

目前有限元分析软件的进步发展及广泛使用给桥梁设计提供了先进的工具，对拱轴线的优化设计也更加方便快捷。利用计算机的强大计算能力，可以在一定的参数范围内反复试算，在确定的约束条件下选取最优的参数，即可以得到最合理拱轴线。

2 最优拱轴系数的拟合

2.1 最优拱轴线的拟合步骤

拱轴线与压力线的偏离是由于受恒载、活载、温度变化、材料的收缩徐变和地基沉降等作用，以及拱圈受荷载压缩变形产生的。虽然拱桥的压力线不定，但是存在两条压力包络线。目前，在工程实践中，采用悬链线、抛物线或高次曲线来逼近恒载加一半活载时的压力线，是一种实用的解决方法。但是，通过计算机的优化计算方法，理论上可以将上述各种参数变量的作用均考虑在内，按照作用的分类及重要程度，求得一条与压力包络线偏差最小的曲线。通过有限元方法求解最优拱轴线，大致有两种思路。其一是通过确定荷载工况，计算令拱圈压力逼近压力线的离散坐标，然后将这些不规则的点拟合曲线得到拱轴线形。另一种则是对荷载工况的要求不高，可以由一种确定的工况来确定，或者由几个工况的包络来确定，各个工况之间还可以通过加权的方式来区分重要性，然后通过反复试算来确定目标函数最小的情况。本文采用的就是第二种方法。

确定最优拱轴系数的拟合过程可分为以下几个步骤:

1)采用恒载加活载时的压力线确定一个初始的拱轴系数。由于恒载加一半活载时的压力线是在实际设计过程中被认可的一个较为合理的值，而一个接近最优拱轴线的初始值可以减少迭代次数，加快迭代速度。

2)用设计变量参数化表达拱轴线方程。通过先假定的拱轴曲线类型，就可以用函数表达拱轴各个离散点的坐标，函数的参数即为设计变量。优化结果的取得是通过改变设计变量的数值来实现的。参数设置上下限作为变化范围，设置步长作为每次改变的量的大小。

3)设置状态变量体现优化的边界条件。状态变量是因变量，是设计变量参数化表达的函数。在桥梁结构设计中，状态变量可以是位移，弯矩或者用来作为判断结构优化与否的任何一个由参数表达的函数。状态变量是用来控制设计的，必须定义足够的状态变量。若状态变量设计的范围过小，也会导致优化设计无法求得合理的解。

4)目标函数。它是最终优化的目的，是设计变量的函数。改变设计变量的数值将改变目标函数的数值。有限元方法就是通过改变设计变量，经过反复试算，在设计变量的变化范围内，求解满足状态变量控制的目标函数，在这一系列的目标函数的解中，寻找极值。

2.2 优化方法和优化准则

优化方法可采用最小二乘法进行拟合。五点重合法求解得出的曲线作为初始曲线，通过内力与拱轴线变化函数的关系，迭代求解得出最优曲线。确定优化方法之后，还需要确定收敛准则。拱轴线的优化过程需要在一定条件下能最大限度的逼近压力线。逼近程度好坏的标准就是优化准则。假设F为目标变量，可以是弯矩或者位移，X为设计变量，在这里是拱轴线函数表达式中的参数。Fj，Xj和Fj－1，Xj－1分别为目标函数和设计变量的第j次和第j－1次迭代结果，Fb和Xb分别是当前最优的目标函数及相应的设计变量值。如果满足︱Fj－Fj－1︱≤τ或者︱Fj－Fb︱≤τ，τ为目标函数的允差，那么认定迭代收敛，于是迭代停止。

在拱桥设计中，最理想的目标是拱圈轴线与压力线在任何截面上的差值τ均达到最小，避免某个截面τ过大而成为危险截面。

3 最优拱轴系数的拟合实例

某拱桥，其跨径L=100 m，空腹式无铰拱，矩形混凝土截面，截面大小5 m×1 m，弹性模量1.95×104MPa(见图1)。

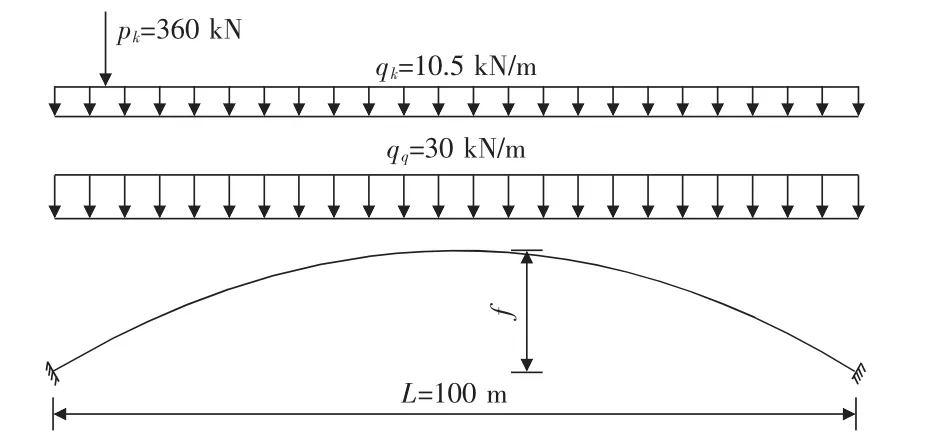
图1 拱桥优化计算简图

为了说明的简单，将恒载设定为均布荷载，大小为300 kN/m，汽车荷载为公路Ⅰ级，单车道，整体升降温以及徐变等影响忽略。由参考文献[1]可知，当外荷载为均布荷载时，即gj=gd，拱轴线接近于抛物线方程。在优化过程中，方程表达式为y=ax2+c，其中c可以用－aL2/4表示。其中参数a即为设计变量，而c则是由a表达的函数，是因变量。活载计算得出最大最小弯矩包络，然后取最大最小弯矩的中间值与恒载弯矩进行叠加，以此弯矩进行优化。优化分析时选取了三种优化准则进行比较，分别是各截面弯矩绝对值之和、弯矩最大值和各截面弯矩的方差。另外，计算了矢跨比分别为5，6，7，8和9时的弯矩分布情况。计算得到优化准则为各截面弯矩绝对值之和最小时，矢跨比为6.47;优化准则为弯矩最大值最小时，矢跨比为6.48;优化准则为弯矩方差最小时，矢跨比为6.49。这三个优化准则得到的矢跨比非常接近，优化结果也相差不多。从图2中可见，矢跨比从9到5的变化基本是一条U形的曲线。三种优化准则计算的结果均为最小。

图2 各截面弯矩最大值

从图3中可见，三种优化准则计算的结果同样均为最小，而矢跨比从9到5的变化也基本上是一条U形的曲线。

由图4可知，当优化条件为弯矩方差最小时，弯矩分布较其他情况时更均匀。图5反映了优化后弯矩最大最小包络的情况。汽车活载的集中力对拱脚弯矩影响很大，因此除了拱脚部分弯矩，其余弯矩均较为均匀。

4 结语

1)通过有限元方法可方便的求解优化问题。由于有限元计算的特性，计算中自动计入了拱肋的轴向变形，对外部作用的调整也非常方便。实例中对荷载作用进行了简化，但若需要，也可方便地施加徐变、温度等其他作用。

2)比较不同的优化准则，可见在抛物线线形之下，三种不同的优化准则求解得出的曲线线形相差不大。但是求解过程中迭代的次数相差较大，以求解弯矩的方差时间最长。

3)最优拱轴曲线对外荷载是敏感的。一般来说，荷载较大时，可得到矢跨比较小的曲线，反之亦然。这和拱肋内力的数值公式计算结果是一致的。

4)由于施加了实际的荷载工况，通过本方法优化计算得到的结果可直观反映成桥阶段的内力。

通过实例，可以看到有限元优化的效果十分显著。并且有限元优化计算方法适应性广，通过修改模型，可以适用于各种类型的拱桥，甚至于其他类型的桥梁结构，是提高工程师工作效率，得到最优结构的有效工具。

[1]顾安邦.桥梁工程[M].北京:人民交通出版社，2002.

[2]JTJ D60-2004，公路桥涵设计通用规范[S].

[3]林阳子，黄 侨，任 远.拱桥拱轴线的优化与选型[J].公路交通科技，2007，24(3):59-63.

[4]周旻昊.常用拱轴线的设计研究[J].公路工程，2010，35(3):92-95.