大型电力变压器内绕组径向屈曲分析

2012-08-21吴明君刘文里李阳阳

黑龙江电力 2012年6期

吴明君，刘文里，李阳阳

(哈尔滨理工大学，黑龙江哈尔滨150080)

0 引言

通常在变压器绕组外部发生短路时，短路电流和漏磁场相互作用下将产生轴向电动力和辐向电动力，轴向电动力将导致绕组沿轴向上发生相对位移，辐向电动力会使绕组发生失稳变形。由于变压器内绕组辐向失稳是造成变压器损坏一个主要原因。因此，为了研究大型电力变压器绕组辐向电动力，本文将变压器绕组简化为力学模型，并对其分别建立3种单跨模型和1种有弹支的多跨模型，进行对比分析和应力计算，以采取相应措施，提高电力变压器抗短路能力。

1 单跨度模型的分析

1.1 特征值失稳理论

本文采用特征值屈曲分析法［1］，虽然线性屈曲分析只能确定结构屈曲载荷的上限，但对分析大型变压器内绕组的变形非常适用。

线性屈曲分析以特征值问题为基础，首先要求解线弹性加载状态P0的载荷位移关系，即给定P0的解，其表达式为

式中:Ke为弹性刚度矩阵;U0为P0加载时所对应的位移。

假设前屈曲位移很小，可给出任意状态(P、U和σ)的增量平衡方程为

式中Kσ(σ)为应力状态下计算出的初始应力矩阵。

假设前屈曲特征是载荷P0的线性函数为

式中λ为比例因子或载荷因子。

于是，有

因此，在前屈曲范围表达的增量平衡方程为

在临界状态时，结构在{ΔP}≈0时变形{ΔU}有所变化，因此方程可写为

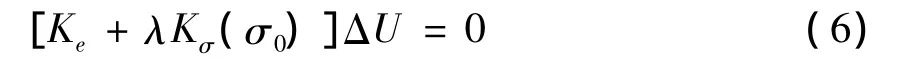
为满足式(6)，需满足

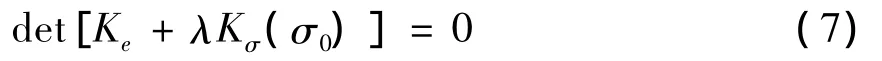
计算最小特征值及其临界载荷Pcr=λcrP0特征矢量，即为其屈曲形状。

1.2 单跨模型的建立

取变压器内绕组径向两支撑之间的线圈作为研究对象，以1台220 kV/180 MVA三绕组变压器为例进行分析，变压器主要参数及低压绕组主要参数如表1、表2所示，图1为3种假设模型:图1a为假定撑条处不发生相对位移及相对转动，即固定支撑形式;图1b为假定导线与撑条的连接处存在相对转动，即假定为铰接形式;图1c是假定变压器撑条为弹性支撑，用弹簧模拟其弹性支撑，并在连接处存在相对转动。

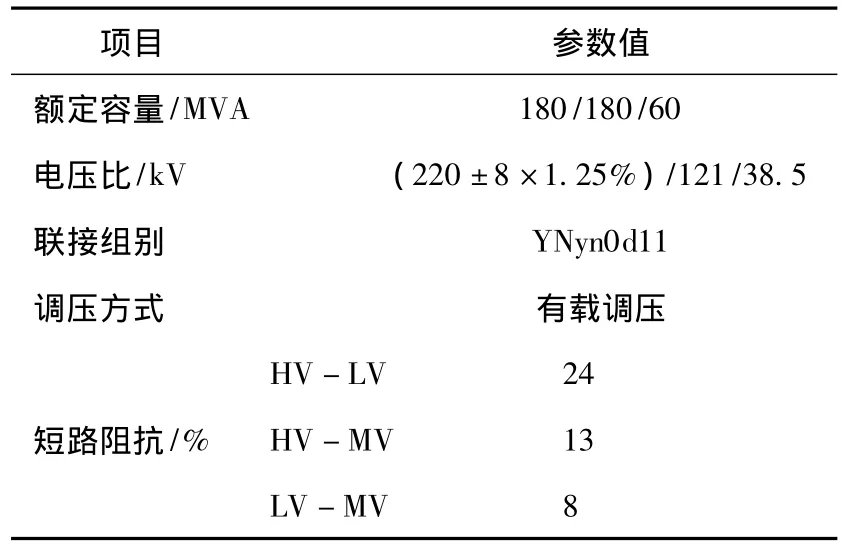
表1 变压器主要参数

表2 低压绕组主要参数

1.3 3种模型的对比分析结果

模型中的约束均为圆柱坐标系［2］，本文中的变压器平均视在压缩力为0.3 kN/cm。将上述3个模型分别进行临界载荷的特征值屈曲分析，结果如表3所示。由表3分析可知，模型图1 a中临界载荷值很大，安全系数为49，与实际情况不符，其原因是固定端的约束条件。在实际运行中，在一定的范围内提高轴向预紧力确实可以增大其临界失稳值，但持续提高轴向预紧力对临界失稳值的提高没有显著的效果。图1b中导线与轴向支撑处有相对转动，其临界载荷值安全系数为13，若用此模型校核变压器内绕组的幅向稳定性是比较危险的，因此将绕组的支撑改为弹性支撑图1c，其临界载荷值安全系数为5。

图1 两撑条间的3种支撑情况

表3 3种模型的结果分析

假设弹簧固定在刚性的圆筒壁上，因此弹簧的底部为全约束条件。弹性支撑的弹性系数若按静态计算可根据力学特性计算求出，同时在静态计算结果的基础上还要考虑实际运行过程中存在撑条和绕组的摩擦系数以及外绕组在变形中对内绕组传递力系数的影响，因此，在模拟时对弹簧的弹性系数进行分析，结果如表4所示。绘出弹性系数K与安全系数的曲线，如图2所示。

由表4分析结果可知，本台变压器若按此方法校核，弹性系数若低于0.3×108N/m，则在承受变压器短路电磁力时将处于十分危险的状况。由图2分析可知，随着支撑弹性系数的升高，其安全系数将逐步增加，当弹性系数趋近无穷时，即为刚性支撑，此时则与图1b模型相近。从位移上可看出，随着弹性系数的增加，位移量反而减小(这里仅研究沿径向的位移，而不考虑总体压力下的总体形变量)。因此，有弹支的模型图1c最贴近实际运行情况，即便使用此种模型校核，其安全系数仍旧较高，但较前两种理想模型而言已有较大的改进。若采用前两种模型进行变压器内绕组屈曲变形的校核是十分危险的。

表4 不同弹性系数下的数值分析

图2 安全系数与弹性系数的关系

2 多跨模型的分析

2.1 模型的建立和临界屈曲

考虑沿绕组圆周方向各种初始不均匀状态对绕组幅向稳定性的影响，本文建立的多跨度弹支模型如图3所示，假设绕组不能沿轴向运动，其余按实际情况约束分析，屈曲图形如图4所示。

图3 多跨模型

2.2 模型结果分析

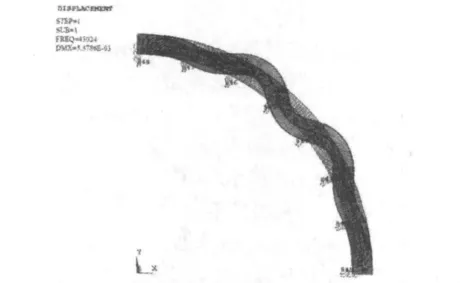
图4 多跨模型的屈曲图

由图4分析可知，其屈曲临界载荷为43.026 kN，平均视在临界载荷为0.548 kN/cm。当撑条的弹性系数为1.0×108N/m时，安全系数为1.83，在其它条件相同的状况下比两端弹性支撑的模型所计算出的临界屈曲载荷值更可靠，其原因是因为多跨度模型考虑了弹性支撑处节点之间位移、转角的连续性和绕组内力相互传递的影响。

2.3 初始缺陷的情况

2.3.1 微扁圆形的初始缺陷

由于在变压器装配过程中存在一些误差，绕组可能存在一些初始几何缺陷［3］。一种较为常见的初始缺陷为绕组在装配中出现的微扁圆情况，如图5所示。在模型中将撑条的弹性系数从1.0×108N/m依次降低到0.65×108N/m，线圈与撑条的紧压度越差，假定的弹簧弹性系数越低，其临界屈曲图形如图6所示。由图6分析可知，一阶屈曲载荷为35.479 kN，平均视在临界载荷为0.453 kN/cm，安全系数为1.51，比整个绕组导线全部紧贴在撑条时的安全系数降低了0.32个百分点。这说明存在几何初始缺陷时绕组的临界屈曲载荷值会降低，导致线圈在较低的电动力下发生失稳。在弹性系数不同时，在最小弹性系数附近，绕组最先发生屈曲变形。因此，在装配过程中尽量保证绕组与撑条之间的紧密结合度和相对位移，对提高绕组在短路电磁力下的临界载荷极其重要。

图5 存在初始缺陷的示意图

2.3.2 相邻匝间空隙的初始缺陷

图6 有初始缺陷的屈曲图

由于变压器绕组由N根导线并联绕制而成，因此在辐向每相邻导线之间存在匝绝缘和匝间空隙。一般认为相邻匝之间导线完全紧靠，但实际绕组过程中因绕制方式、预紧力大小等因素导致导线之间完全紧靠没有空隙。本文实例中变压器的低压绕组是12根导线并联，因此分为3种模型进行分析，如图7所示。图7a中假设低压绕组的线匝辐向上存在1处间隙，将12根导线分为两部分(即内、外各6根导线)，绕制方式按卧绕，则其绕组辐向裕度为1.03，空隙尺寸为1.2 cm;图7b中假设绕组辐向上存在2处间隙，将12根导线分为3组(即内、中、外各4根)，空隙为0.6 cm;图7c中假设绕组辐向上存在3处间隙，将12根导线分为4组(每组3根)，空隙为0.4 cm。

图7 绕组存在初始缺陷的示意图

在弹性系数及其它条件不变的情况下，图7a中得到的临界载荷为33.87 kN，安全系数为1.48;图7b中得到的临界载荷为32.95 kN，安全系数为1.44;图7c中得到的临界载荷为31.69 kN，安全系数为1.39。可见绕组的导线之间存在的空隙越多，在承受短路电磁力时的抗弯曲能力越差，在较小的短路电磁力下就会达到临界载荷，使安全系数有所降低，不发生屈曲变形也会产生累积变形，使圆周方向上的预紧力分布更加的不均匀，对大型电力变压器抗短路能力是十分不利的。因此，使用先进的绕制方式提高其安全裕度是十分重要的，许多厂家已经采取了相应的措施，如将卧式绕制方式改进为立式绕制方式，辐向计算裕度可提高至1.01，这样可减少导线与导线之间的空隙，提高了电力变压器绕组抗短路电磁力的能力。