基于安全性判据及不确定性的输电系统规划方法
2012-08-21徐鹏程芦晶晶李一白温佳鑫
徐鹏程,芦晶晶,李一白,温佳鑫
(1.东北电力大学电气工程学院,吉林吉林132012;2.中国电力科学研究院发展策划办公室,北京100192;3.吉林省四平市供电公司调度所,吉林四平136000)
0 引言
多阶段输电系统规划的主要目标是规划电网结构,对补偿类型、接入的位置和时间进行规定,保证高质量的电力传输。其作用是确保电力系统能够满足预测的需求和安全性判据,从规划的角度最大限度降低投资运行和停运成本。
解决TEP问题必须考虑到TEP问题的多阶段特性,需要确定输电系统补偿的可能方案。为了简化这一难题,简化分析(又称静态分析)假定新的输电设施只在一个阶段内进行安置。文献[1]提出了采用遗传算法解决TEP问题,文献[2]采用了进化策略算法进行求解,文献[3]则采用差分算法。然而这些文献均未考虑到TEP的多阶段特性,而文献[4-5]虽然考虑了这一特性,但未考虑对于不确定性进行处理。
本文基于安全性判据,考虑到TEP问题的多阶段特性,以及对如负载/发电增加等外部不确定性的处理,提出了解决多阶TEP问题的新方法,并用一个实际输电网络验证了方法的实效性。
1 输电系统规划问题
1.1 问题表述
TEP问题的表达式为(其对应备选规划方案k)

式中:n表示可接入补偿的网络支路数量;y为对应规划期的阶数;指基础网络结构下t阶和l支路的补偿总数。
对于由y阶组成的特殊规划期间,一旦找到方案k,多阶段TEP问题的目标函数可表示为

式中:f(Sk)代表现值条件下k矩阵的总成本函数;e代表折扣率;h(t)对应着t阶年份与基准年份之间数值的差异函数;Wl是节点i和j之间的支路l上接入补偿的投资成本;指在k方案的t阶l支路安置的补偿数目;α为甩负荷损失;rt为失负荷损失;代表 k方案中 t阶的有功损耗的运行成本。
1.2 确定性方法
由式(1)可以看出,TEP问题的目标不仅是寻找一个使投资和运行成本最小的规划方案,而且需要保证供给用户足够质量的电能,因此在实际网络中安全性判据的考虑是必不可少的。
通常情况下,安全性判据是通过“N-1”、“N-2”确定性方法体现的,而关键之一在于如何应用。另一关键点是在整个优化过程中将“N-1”准则作为约束考虑。在此情况下,优化过程找到的最佳规划方法不仅应满足完整的网络判据,也应对任一元件进行切除或故障处理。然而,对于大型网络,其计算量相当巨大且会导致额外的投资。因此,使用“N-1”确定性判据时,规定仅在系统的最重要区域使用,即网状网络、主要支路以及互联网络。
1.3 外部不确定性
近年来,电力企业已经做出了结构性转变[6],大量与之相关的不确定性已经出现:未来负荷的增长、燃料价格、发电机类型和位置、系统中不同补偿的成本。这些外部不确定性不能根据过去信息或统计规则进行描述,所以很难对它们进行建模。
解决不确定性的方法之一是采用灵活的规划方案,能够迅速适应带有合理成本的原始规划,而且独立于任何系统结构变化。为达到这一目标,不确定性可采用多种方案技术和模拟树、和/或模糊集[6-7]表示。
2 优化方法
启发式算法[1,5]已经证明在解决某些问题时可求得高质量解的潜力,当然其中也包括TEP问题。进化算法指使用生物进化中如复制、突变、重组(交叉)和选择等方式的一系列进化计算。这些算法中,个体的数量表示解决方案,由应用程序在进化过程中进行实时修改。现在有很多优化算法具备这些特征,如遗传算法、进化策略算法和差分算法。本文提出采用进化策略算法的简要模型。
与遗传算法中合并、重组和突变的方法不同,进化策略算法仅需要有变异因子,在一个规划t阶内的表达式表示如下:
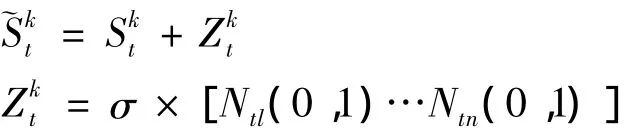
3 算例分析
构建一个小型网络,该系统由20个节点和33条电路组成。在参考年份,装机容量为465 MW,峰值负荷为248.4 MW。图1表示了一个简化的系统,包含规划年的最佳规划方案。其目的是在规划期间得到将节点“1832”接入138 kV系统的最优规划方案。系统规划期分为8阶并且对于每阶将有平均7.7%的负荷增长,这将导致最后一年峰值负荷为343.7 MW。在分析中不予考虑N-1安全标准,但会考虑可靠性方面。
3.1 等效系统
为确定等效系统,需定义内部及外部系统。内部系统是所需区域节点组成的集合,即需要进行规划的区域;外部系统是使用WARD法等效削减具有注入功率节点的区域组。对注入功率,负值代表负荷,正值代表电源。最后,在每个边界节点将有一个10%的增长用来模拟最大发电能力,反映内部系统发生的突发事件。假设等效电路无容量限制。
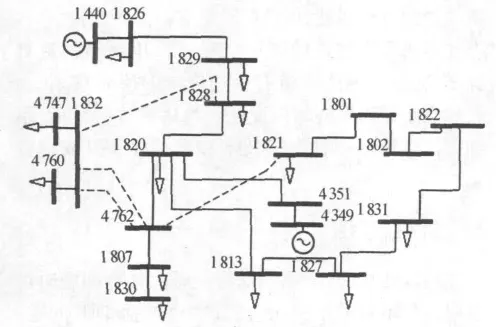
图1 方案I的单线图
3.2 优化方法
等效系统定义后,在规划期间应用优化方法,可得到到使投资和运行成本最小化的一些最优规划方案。这些工具用来协助规划者建立一套初始的规划方案,方案在考虑不确定性并在交流潮流模型下计算。对于实际传输网络(图1),所有节点之间的距离小于60 km并且在每个路权区域满足3条平行的线约束条件,所以138 kV的所有节点的连接均是可行的。使用进化策略算法作为优化方法,在这个实际系统中使用相同的参数。与有功损耗相关的运行成本使用以下参数:CkWh=0.10US$/kW·h,LF=0.5。
3.3 可靠性研究
这里考虑通过优化方法选出最优方案,并用非序贯蒙特卡洛仿真计算可靠性指标,最终目标是最小化总成本,包括投资成本、运行成本及停电损失成本(即指标LOLC)。为得到指标LOLC,实验中假定一个独立网络的停电成本为1.50US$/kW·h,并考虑峰值负荷。表1中表示了通过进化策略算法找到的5个最优方案的现值成本。有功损耗的运行成本,对应于通过进化策略算法找到的最佳方案A的现值计算结果的差异。此时方案A具有以下补偿:1条连接节点1 832与4 762的传输线(接入于参考年)以及在规划期第二阶段接入的2条线(1994年—2001年和2001年—2005年)。
表1列出的所有方案均有3个补偿,而其各自的位使指数LOLC从10.02×106US$变为22.19×106US$。可见,可靠性评估在求解最佳方案上起到了决定性作用。
3.4 交流潮流分析
通过优化方法得到的方案,还需使用交流潮流模型进行评估。分析中,能观察到传输负荷以及节点电压幅值的变化。优化方法基于直流潮流,而交流潮流模型是用来判别是否产生由于某些电路中的无功功率导致最佳方案中节点的过电压问题。其中一个方案为更优的规划方案。
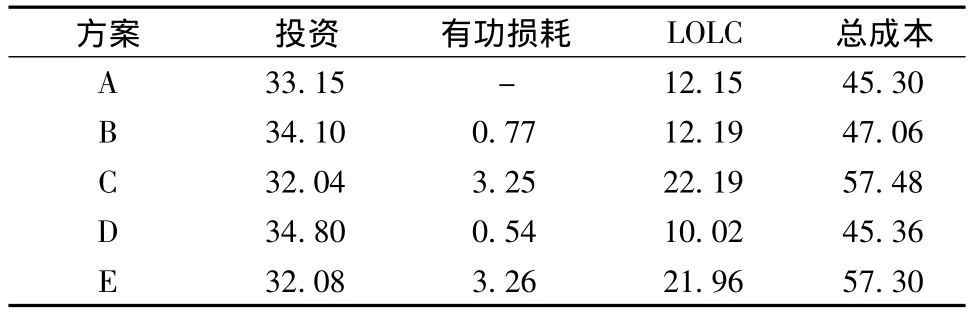
表1 5个最佳方案的现值 106US$
表1提到的3个最佳方案(A、B和D)考虑了当前总成本现值,是用交流模型评估的。如表2所示,3个最佳方案的电压平均值满足系统的限制(0.95~1.05 p.u.),传输负荷对应总传输容量的34%。只有传输网络和系统内部节点考虑这种评估,观察是否存在无电压值或超出传输容量的情况,并且该评估必须考虑到总成本现值。

表2 电压和传输容量平均值
3.5 外部不确定性
考虑总成本和交流负荷潮流所得的最佳方案,最终评估还要考虑外部不确定性。多种方案技术可用于处理负荷增长的不确定性,也可用于处理其他参数的不确定性,如折扣率和终端成本。负荷增长不确定性的规划研究考虑了3种不同的情况(每种情况由内部系统的年负荷增长定义):1)负荷增长较低(平均年负荷增长5.5%);2)负荷增长普通(平均年负荷增长7.7%);3)负荷增长较高(平均年负荷增长10.1%)。
图2表示了所有情况下内部系统的负荷增长。内部系统的最大发电容量保持不变,边界节点的发电容量由每种情况下外部系统等效模型定义。
在普通情况下,可采用该过程使表1得到的最佳方案反复在较低情况与较高情况下寻找最佳方案。表3表示了在较低与较高情况下,3个最佳方案的现值成本。该方案的运行成本将作为每种情况下最佳方案的参考运行成本。决定性判据最低预期成本和最小费用最大流算法用来判定所有情况下的最佳方案。通过这些判据得到的最佳方案必须在其它情况下评估,如果需要,可采用一些改进使它们适应新的情况。通过这些判据,还可以计算不同情况下所选方案的灵活性以及鲁棒性。

图2 较高、普通和较低情况下内部系统负荷增长

表3 负荷增长较低和较高情况下3个
表4列出了最低预期成本确定性原则的结果。负荷增长较低、普通以及较高情况发生的概率分别为0.25、0.50、0.25。可以看出,策略A具有最低的期望成本,因此是所考虑情况中最佳的。

表4 总花费以及额外花费 106US$
此外,每个情况下的最佳策略是在各自的情况下产生的,这证明了进化策略算法在寻找每种情况下最佳方案是高效率的。表5列出了最小费用最大流算法确定性判据。

表5 最大值列表 106US$
与最低预期成本确定性判据不同,使用最小费用最大流算法时,方案I为最优方案。从表4和表5可以看出,由于方案I的额外投资比方案A略高并且最值小于方案A,所以方案I为最佳方案,可见方案的最终选择取决于网络的风险评估。
4 结束语
本文提出的解决多阶TEP问题的新方法使用了安全性判据,对不确定性进行处理,简化了问题模型;使用适当优化算法进行计算,降低了计算难度且结果精度满足要求;从计算的角度及传输补偿方案的角度,证明了该方法的实效性。
[1]GIL H A,DA SILVA E L.A reliable approach for solving the transmission network expansion planning problem using genetic algorithms[J].Electr Power Syst Res ,2001,58:45 -51.
[2]BINATO S,OLIVERIRA G C,ARAUJO J J.A greedy randomized search procedure for transmission expansion planning[J].IEEE Trans Power Syst,2001,16:247 -253.
[3]DONG Z Y,LU M,LU Z,et al.A differential evolution based method for power system planning[C]//IEEE congress on evolutionary computation.Vancouver,2006:2699-2706.
[4]XU Z,DONG Z Y,WONG KP.Transmission planning in a deregulated environment[J].IEE Proc Gener Transm Distrib,2006,153:326-334.
[5]ESCOBAR A H,GALLEGO R A,ROMERO R.Multistage and coordinated planning of the expansion of transmission systems[J].IEEE Trans Power Syst,2004,19:735 -744.
[6]CIGRE W G.Dealing with uncertainty in system planning—has flexibility proved to be an adequate answer?[J].ELECTRA,1993,151:53-65.
[7]CIGRE W G.Methods for planning under uncertainty—towards flexibility in power system development[J].ELECTRA ,1995,161:143-164.
