人-车-路闭环系统下的车辆稳定性研究

刘志强，廉 飞 ，茅峻杰，吕 学

(江苏大学汽车与交通工程学院，镇江 212013)

车辆电子稳定性系统是车辆的主动安全系统，它综合了制动防抱死系统，驱动力控制系统和横摆力矩控制系统，使行驶车辆的安全性得到很大的提高.近年来，车辆电子稳定性系统一直是国内外研究的重点，但多数研究处于开环系统平台上，利用现代控制理论的一些方法，对电子稳定性系统进行研究[1-4].文中在人-车-路闭环系统中研究车辆电子稳定性程序.

1 闭环系统的建立

1.1 车辆动力学系统模型

汽车作为一个整体，是一个多自由度非线性系统，为了简化问题，建立7自由度的车辆模型[5]，包含车身纵向、横向、横摆的运动和4个车轮的旋转运动.对所建立的模型做如下假设:①固结于汽车上的动坐标系原点与汽车质心重合;②忽略悬架的作用，汽车没有垂直运动;③汽车绕Y轴的俯仰角及绕X轴的侧倾角为0;④各轮胎的机械特性相同.整车力学模型可简化为图1.

纵向动力学方程

横 (侧)向动力学方程

横摆运动方程

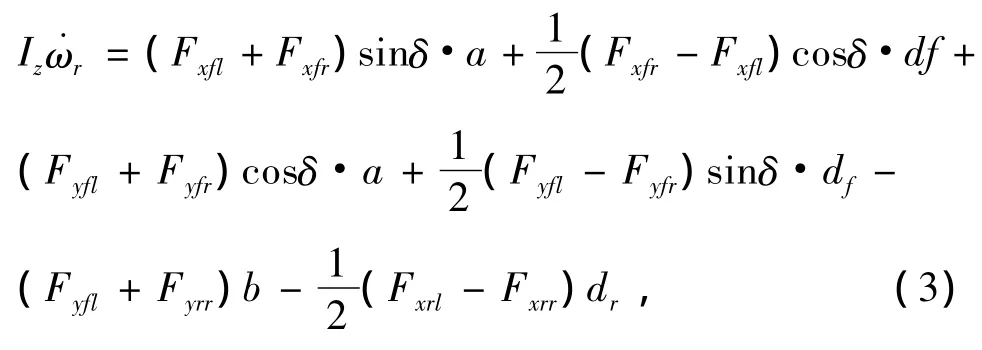
式中:M为整车质量;Vx为汽车纵向速度，Vy为汽车侧向速度，ωr为汽车的横摆角速度;Fxfl，Fxfr，Fxrl，Fxrr分别为左前轮，右前轮，左后轮，右后轮纵向力;Fyfl，Fyfr，Fyrl，Fyrr分别为左前轮，右前轮，左后轮，右后轮侧向力;δ为前轮转角;Iz为车辆转动惯量;df，dr为前后轮轮距;a，b为质心到前后轴的距离.

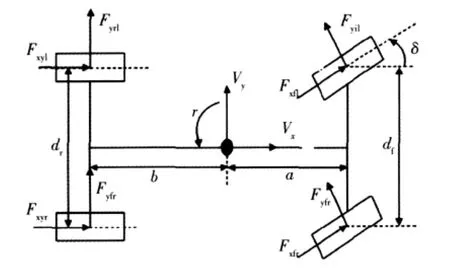
图1 整车动力学模型

1.2 轮胎模型

采用魔术公式 (H.B.Pacejka模型)[6]建立轮胎模型.魔术轮胎公式对轮胎力的表达式比较统一，拟合精度高，适用于汽车动态模拟和实验对比.魔术公式轮胎的一般形式如下

式中:Y可以为侧向力、纵向力或者回正力矩;X表示侧偏角α或纵向滑移率λ;D为巅因子;B为刚度因子;C为曲线形状因子;E为曲线曲率因子;忽略车轮侧倾角的影响.

根据魔术公式，轮胎侧向力计算公式为

轮胎纵向力计算公式为

轮胎测、纵向力计算所需的拟合参数如表1、表2所示.

表1 魔术公式轮胎模型侧向力计算的各拟合参数

表2 魔术公式轮胎模型纵向力计算的各拟合参数

由上述公式，在MATLAB/Simulink中建立轮胎模型.根据所建立的车辆动力学数学模型，在MATLAB/Simulink环境下建立整车动力学模型.整车参数选用某小型车的数据:整车质量M=1 580 kg;质心到前轴距离a=1.237 m;质心到后轴距离b=1.303 m;车辆转动惯量Iz=2 350 kg·m2;前轮距df=1.40 m;后轮距dr=1.42 m;车轮半径R=0.317 5 m;车轮转动惯量Iω=2 350 kg·m2.

1.3 驾驶员模型

采用单点预瞄最优加速度 (最优曲率)驾驶员模型.确定驾驶员模型的原则是最小误差原则:使汽车的运动尽可能与预期的轨道相一致.图2是单点预瞄最优曲率 (最优加速度)驾驶员模型:t时刻，汽车具有的即时状态为y=y(t)，˙y=˙y(t).驾驶员向前预视一个距离d，对应于“预瞄时间”T=d/v，通过车轮转角δ(或方向盘转角δsw)选择一定的运动曲率，使t+T时刻汽车的横向位置y(t+T)与预期轨道坐标 f(t+T)一致，即y(t+T)=f(t+T)[7].

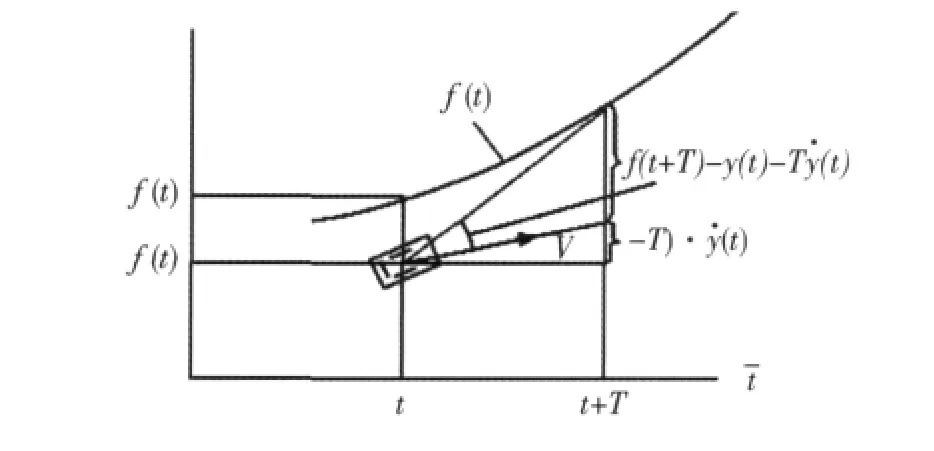
图2 单点预瞄最优加速度驾驶员模型

由上述原理，结合“Aeklman几何原理”(即汽车轨迹曲率与方向盘转角成正比:)，得到理想的方向盘转角为

单点预瞄驾驶员模型对汽车大方位角行驶时的方向进行控制是可行的.

2 ESP控制系统

2.1 2自由度车辆参考模型

2自由度线性单轨模型[8]可以反映驾驶员转向输入与车辆横摆角速度、质心侧偏角之间的线性关系，可将其稳态转向特性作为汽车稳定性的理想状态.

2自由度线性模型为

式中:M为车辆质量;δ为前轮转角;Fy1，Fy2为地面对前后轮的侧向力，Iz为汽车绕Z轴的转动惯量.根据坐标系的规定，前后轮的侧偏角分别为

式中:β为质心侧偏角，β=Vy/Vx.

将2自由度车辆模型的质心侧偏角作为参考值.

2.2 车辆稳定性程序的模糊控制

以7自由度车辆质心侧偏角为控制变量，基于模糊控制的理论，以质心侧偏角的参考值和实际值之差e和质心侧偏角和实际值之差的变化率ec为输入变量，以产生的需要加在车体上的横摆力矩M为输出变量.

取误差e，误差变化率ec及输出变量M的论域范围都为 [－1，1]，隶属度函数取5个，分别为NB(负大)、NS(负小)、Z(零)、PS(正小)、PB(正大).各自的论域范围，e的量化因子Ke=1，ec的量化因子Kec=0.5，M的量化因子Km=5 000.

模糊规则是决定模糊控制器性能的关键因素，它用语句的方式描述控制器输入输出变量之间的关系，一般根据经验来设计.模糊控制采用“Mamdani”方法.推理为“max-min”方法，去模糊方法为面积重心法.

模糊逻辑控制规则如图3所示.

图3 模糊控制规则

驾驶员模型将道路模型输入变换为车辆前轮转角δ，作为闭环模型的初始输入，7自由度车辆模型反馈车辆侧向速度，侧向位移，横摆角速度，质心侧偏角等.驾驶员模型与整车模型组成闭环控制系统.

3 仿真结果与分析

基于MATLAB/Simulink软件环境，将所设计的质心侧偏角的模糊控制器装配到已建立的7自由度动力学闭环系统上 (见图4)，进行模糊控制系统的整车仿真实验.

采用ISO标准中规定的“紧急双移线”试验.为了能够更好地体现汽车稳定性控制的效果，路面的附着条件系数设为0.5的路面，基准车速设为60 km/h，驾驶员模型预瞄时间T=0.4 s.在上述仿真实验环境中，车辆行驶轨迹如图5所示.

图4 仿真实验闭环系统

图5 车辆行驶轨迹仿真图

从图5车辆行驶轨迹得知，该驾驶员模型有较好的道路跟随能力，在电子稳定性系统 (ESP)的帮助下，车辆能按照路径正常行驶，保证车辆的操纵稳定性.

图6－7分别是“紧急双移线”仿真实验过程中，车辆的质心侧偏角和横摆角速度的对比结果.

图6 双移线侧偏角对比

由图6可知，无电子稳定性系统控制的车辆侧偏角在5.5秒过后相比有电子稳定性系统控制的侧偏角迅速增大;而此时无电子稳定性系统控制的车辆横摆角速度也明显变大，车辆失稳.通过电子稳定性系统的主动介入，可控制车辆在安全范围内行驶.

从图7可知，相对于带电子稳定性系统控制的车辆，在5.5 s后，不带电子稳定性系统控制的车辆横摆角速度迅速增大，严重影响车辆的操纵稳定性.

图7 双移线横摆角速度对比

4 结论

利用MATLAB/Simulink建立了人-车-路闭环系统及车辆电子稳定性系统的仿真平台.通过仿真分析可得.

1)7自由度车辆模型可以合理的反应车辆的动态响应，采用“魔术公式”建立的轮胎模型可以拟合复杂的轮胎力.

2)单点预瞄最优曲率驾驶员模型能够较好的描述驾驶员的方向控制行为.

3)闭环系统中，车辆在ESP系统的作用下，能较好的提高其操纵稳定性，有效防止侧滑等危险工况的发生.车辆安全性能达到更高的水平.

[1] Masato A，Yoshio K，Kazuasa S，et al.Side-slip control to stabilize vehicle lateral motion by direct yaw moment[J].JSAE，2001，22(1):413-419.

[2] Chou H，Novel B D.Global vehicle control using differential braking torques and active suspension forces[J].VehicleSystem Dynamics， 2005， 43(4):261-284.

[3] 宗长富，郑宏宇，田承伟，等.基于直接横摆力矩控制的汽车稳定性控制策略 [J]，吉林大学学报，2008，38(5):1010-1014.

[4] 马春卉，吴志林，王良模，等，汽车ESP系统的建模和控制方法 [J]，南京理工大学学报，2010，34(1):108-112.

[5] 贾豫东，宋 健，孙 群.用于电子稳定程序的汽车模型和控制策略 [J].公路交通科技，2004，21(5):132-136.

[6] PACEJKA H B，BESSELINK I J M.Magic formula tyre model with transient properties[J].Vehicle System Dynamics，1997，27(1):234-249.

[7] 李昌刚，武建勇，唐厚君，等.基于底盘集成控制的人-车闭环系统对对提高车辆操纵稳定性和路径跟踪能力的效果研究 [J].汽车工程，2009，31(9):812-819.

[8] 喻 凡.汽车系统动力学[M].北京:机械工业出版社，2005.