圆柱形基阵指向性仿真研究

张雨强，侯 朋，夏春艳，余 珍

(大连测控技术研究所，辽宁 大连 116013)

0 引言

舰船辐射噪声是评价舰船隐蔽性的重要指标之一。随着减振降噪技术的发展，舰船辐射噪声越来越低，传统的无指向性单点水听器测量方法已难以满足对当前低辐射噪声目标的测量要求。采用垂直阵可以获得空间增益，提高接收信号的信噪比［1］，但对于浅海环境下的应用，要获得足够的测量增益就需要非常大的基阵尺寸，这对于低频高增益测量将产生一定的影响。采用矢量传感器可以以较小的尺寸完成低频信号的测量，并达到较高的测量增益，但其获取测量增益的能力受海洋环境声场性质的影响较大，矢量信息处理较为复杂。另外，矢量传感器受其制造能力的限制，高频测试能力有限［2］。

近年来，宽频带、高增益体积阵在舰船辐射噪声测量中崭露头角［3－4］。体积阵的阵元在空间上立体分层分布，布放方式十分灵活，所构成的基阵结构更加紧凑，有利于基阵尺寸的小型化，并且参与波束形成的阵元众多，可大大提高测量增益，为浅海条件下进行低噪声测量提供一种有效手段。本文从舰船辐射噪声测量的角度出发，以圆柱形体积阵为例建立数学模型，仿真分析圆柱形基阵的空间指向特性及其提高测量增益的能力，讨论影响基阵指向特性的各个因素之间的关系，给出基阵波束图的控制方法以提高基阵的性能。

1 数学模型

考虑由T=N×M个各向同性阵元组成的圆柱形基阵接收位于基阵远场点信号源辐射的声波，如图1所示。其中，N为圆阵的数目，M为每个圆阵的阵元数目。假定以坐标原点O为参考点，圆柱的底端位于xoy平面上，圆阵的圆心位于z轴。图中，2个圆阵之间的距离为d，半径为R，圆周上相邻两阵元之间的弧长为ds，则第n个圆周上第m个阵元的位置向量为

式中:n=1，2，…，N;m=1，2，…，M。

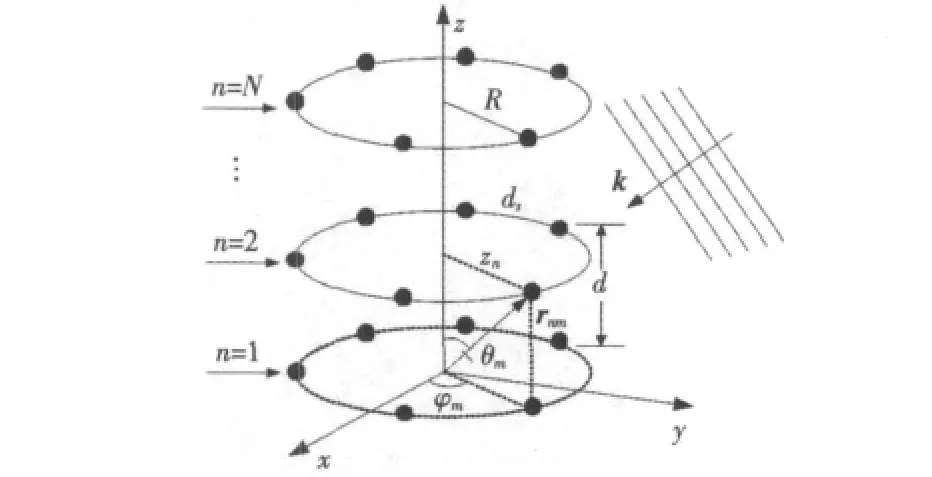
图1 圆柱形基阵几何结构示意图Fig.1 Geometric configuration of cylindrical array

若单频平面波从k方向入射到基阵

式中k0=2π/λ，则基阵对单频平面波信号的频率－波束响应可表示为

式中:A(θ，φ)为基阵对极角为θ、方位角为φ的来波的频率－波束响应;wnm和gnm为第nm个阵元的幅度权值和角度灵敏度;(θs，φs)为基阵的指向方向。

基阵的指向性指数定义为:基阵在理想的各向同性噪声场中，接收完全相关的信号，经过波束形成后输出信噪比相对自由场中无指向性阵元输出信噪比改善程度的分贝数［5－6］。根据式(1)～式(3)，可以求得各向同性噪声场下圆柱阵的指向性指数。

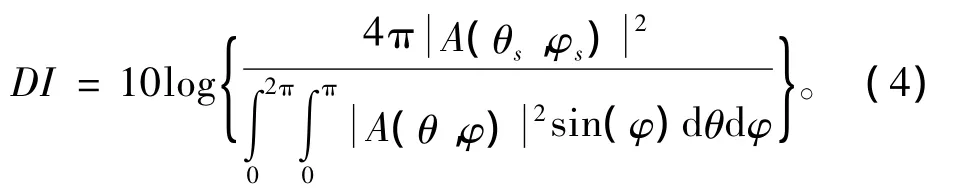
式(4)分母中的双重积分求解比较复杂，可以通过如下的数值计算方法予以解决［6］。为了计算方便，定义

对于内层积分，使用高斯一勒让德积分公式进行计算;对于外层积分，用梯形公式进行计算，则式(6)可转化为

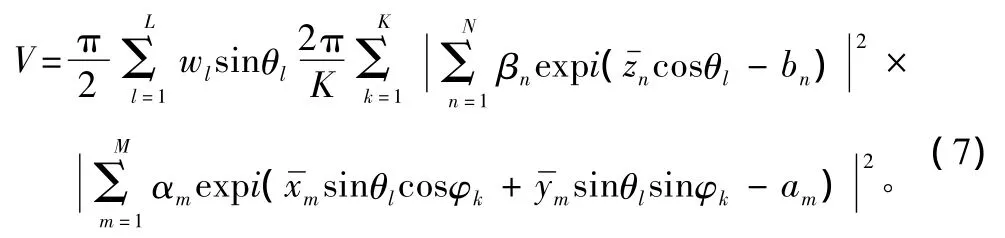
其中 {wl}为L个高斯权值。

式中 {tl}为L阶勒让德多项式的L个0点。

式(7)所示的表达式即为双重积分的精确数值近似，其求解完全可以利用Matlab中已有的函数进行计算。当基阵的阵元数较大时，上述指向性指数计算方法效率极高。

2 数值仿真与结果分析

2.1 指向性与基阵几何结构的关系

以图1所示的圆柱形基阵为例进行仿真，利用式(7)计算圆柱阵的指向性指数。为便于计算，仿真中假定噪声场为理想均匀全向噪声场，阵元均为无指向性阵元，即阵元的角度灵敏度gnm(θ，φ)均为1，各阵元的幅度加权采用均匀加权，即wnm=1/T，T为总阵元数。

2.1.1 指向性指数与阵元数之间的关系

假定基阵在设计频率处的指向性指数达到20 dB可以满足系统设计要求。选取基阵的设计频率f0=4 kHz，声速为1500 m/s，阵元间距d=ds=λ0/2(λ0=c/f0为声波波长)，基阵的圆阵个数与单个圆阵上的阵元数目相等，即M=N。图2给出了圆柱形基阵指向性指数随阵元数的变化关系曲线。为便于比较，图中给出了直线阵和平面阵的指向性指数随阵元数的变化关系曲线，其中，选取平面阵长与宽的阵元数相等。同时，图中还给出了经验公式的预报结果［7］，以验证上述计算结果的可靠性。

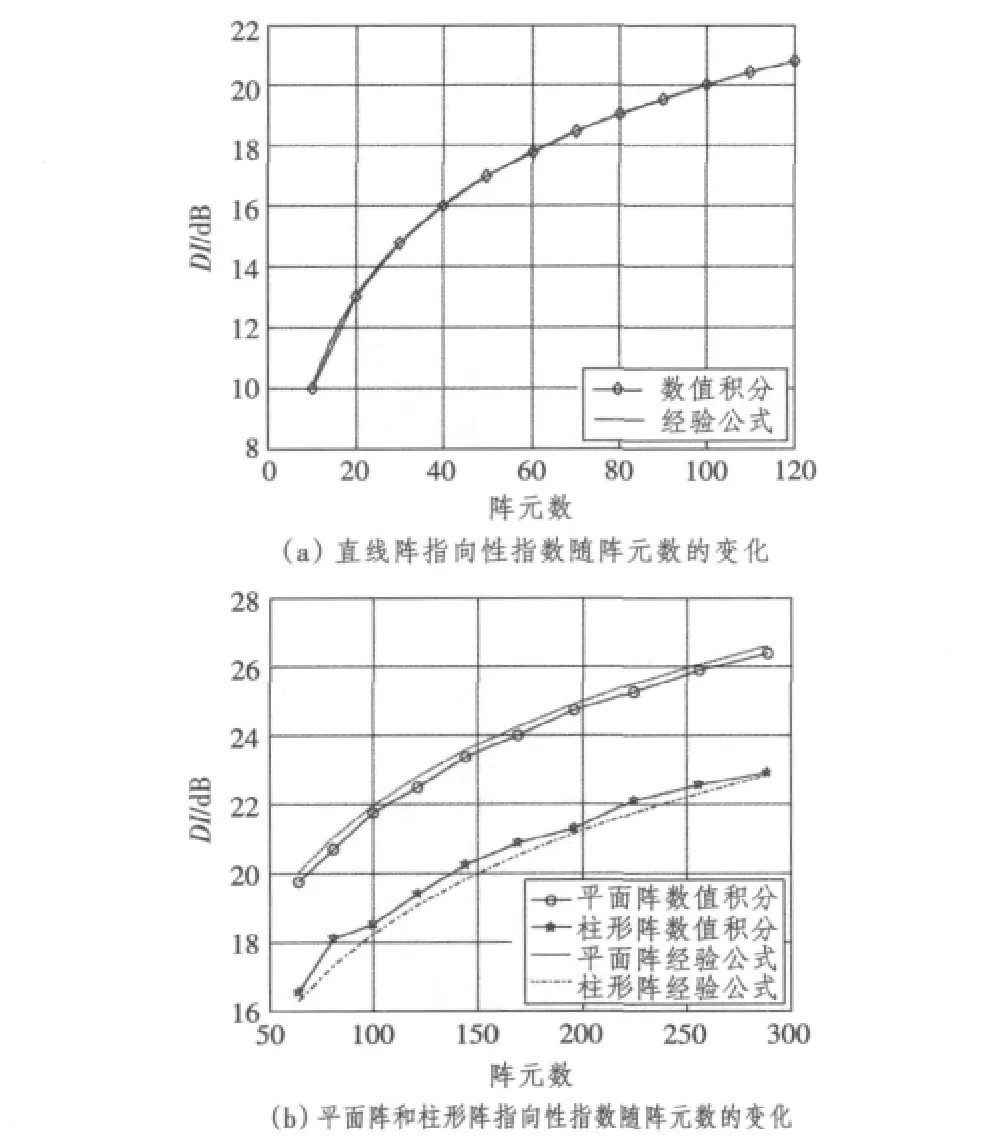
图2 基阵指向性指数随阵元数的变化曲线Fig.2 The relationship between array's DI and elements number

从图2可以看出，几种阵型的指向性指数都随阵元数的增加而逐渐增大，但增大的速度越来越缓慢。在相同条件下，若要基阵的指向性指数达到20 dB，则直线阵约需100个阵元，柱形阵约需140个阵元，平面阵仅需80个阵元。然而，就直线阵而言，大量的阵元必定造成较大的基阵尺寸，这不利于系统的布放与回收，同时致使阵体易受海流冲击的影响，增大阵元位置误差。尽管平面阵具有较好的指向性，但当其扫描角度大于一定值时，基阵的性能会变差［8］。在低频应用范围内，系统面积较大，容易存在布放困难等问题。圆柱形基阵可以提供较高的测量增益和空间分辨能力，它是以牺牲阵元数目和增益能力为代价来获得较小的基阵尺寸，由于受表面曲率的影响，在相同阵元数的情况下，柱形阵的指向性指数比平面阵约小3 dB。

2.2.2 指向性指数与频率之间的关系

假定要求基阵在设计频率f0=4 kHz时的指向性指数为20 dB。选取阵元数为180，波速为1500 m/s，阵元间距d=ds=λ0/2(λ0=c/f0)，柱形阵圆阵个数和每个圆阵上阵元数为12×15(柱形阵高约为2 m，直径约为0.9 m)，数值考察柱形阵工作在0.5～8 kHz时的指向特性随频率的变化关系，仿真结果如图3所示。图中给出了平面阵的指向特性随频率的变化关系曲线，其中平面阵的长宽阵元数为15×12。

图3 基阵的指向性随频率的变化关系Fig.3 The relationship between array's DI and frequency

从图3可以看出，在一定的频率范围内，随频率的递增，柱形阵和平面阵的指向性指数整体上呈递增趋势;超过一定的频率时 (如7.5kHz左右)，指向性指数开始呈下降趋势。2种阵型工作在较低频率时，其指向性指数相差不大。值得注意的是，尽管随着频率的升高，基阵的指向性指数逐渐增大，但伴随着阵元间距趋于λ，基阵的波束图中会出现过多的旁瓣，因此，对于高于设计频率的情形，基阵提高增益的能力有待商榷。

2.2 基阵的波束方向图

为了便于分析，假设式(3)中权值wnm是可分离的，且各阵元均为全向性阵元，则式(3)可表示为

式中:wn为第n个圆阵的加权值;wm为每个圆阵上第m个阵元的加权值。显然，式(9)中的第1项为直线阵的波束方向图，而第2项则恰为第n个圆阵的波束方向图，即圆柱阵的波束方向图为直线阵的波束方向图和圆阵的波束方向图的乘积［8－9］。

基阵的－3 dB波束宽度反映基阵对目标的方位分辨能力，旁瓣级反映基阵抑制噪声干扰和假目标的能力。因此，根据式(9)可以求得，在均匀加权及权系数可分离的情况下，垂直方向及水平方向的－3 dB波束宽度和旁瓣级的表达式如下［10］:

垂直方向直线阵－3 dB波束宽度

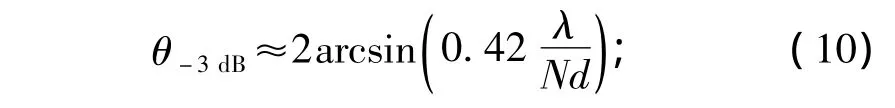
垂直方向的旁瓣级

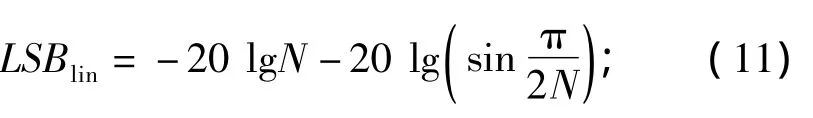
水平方向圆阵－3 dB波束宽度

水平方向的旁瓣级

式中φ0为出现第一旁瓣的方位角。

2.2.1 常规波束形成波束图

假设基阵阵元数为N×M=12×15=180，阵元间距 d=ds=λ0/2，基阵指向方向为(θs，φs)=(90°，0°)，声速c=1500 m/s，根据式(9)得到常规加权下的圆柱形基阵波束方向图如图4所示。

图4 圆柱形基阵波束方向图Fig.4 Beam pattern of cylindrical array

从图4可以看出，圆柱形基阵在垂直方向和水平方向均具有指向性，且在整个扫描角度范围内具有一定的对称性，综合了直线阵和圆阵的优点;改变基阵的指向方向(θs，φs)，就可以使波束主瓣出现在想要的位置，实现了在垂直方向180°和水平方向360°范围的空间全方位扫描，消除了空间方位模糊，可以更好地抑制噪声和干扰，进而提高测量精度和测量增益。根据式(9)～式(13)，表1和表2给出了基阵的－3 dB波束宽度和旁瓣级随阵元数和接收信号频率的变化关系，其中f0为基阵的设计频率，从仿真结果可以看出，所设计基阵的指向性有以下特点:

1)如表1所示，当基阵接收信号频率不变时，垂直波束宽度随垂直方向阵元数N的增加而减小，水平方向上阵元数M的变化对其影响不大;相应地，水平波束宽度受垂直方向阵元数N的影响很小，而随着水平方向阵元数M的增加而减小。

2)如表2所示，在基阵接收频率不变的情况下，垂直方向旁瓣级随垂直方向阵元数N的增加而减小，但变化的幅度不大;当N很大时，垂直方向旁瓣级趋近于－13.5 dB;而垂直方向旁瓣级几乎不受水平方向阵元数变化的影响;水平方向的旁瓣级基本不随垂直方向和水平方向阵元数的变化而变化。

3)从表1和表2中可以看出，在阵元数和阵元分布以及基阵设计频率不变的情况下，垂直方向和水平方向的波束宽度都随接收信号频率的增加而减小;而垂直方向和水平方向的旁瓣级受接收信号频率的变化影响较小。

综上所述，当设计圆阵形基阵时，应根据实际应用中技术指标要求 (比如波束宽度、旁瓣级、工作频率等)，来确定基阵的阵元数，综合调整阵元的空间分布，用最少的阵元达到最优的基阵性能。与此同时，还可以看到圆柱形基阵在均匀加权情况下的一个明显缺点:水平方向旁瓣级过高，不能很好地抑制噪声和干扰，这样就必须采用其他加权方法来降低旁瓣级。

2.2.2 旁瓣控制波束形成波束图

利用幅度加权方式可以降低基阵的波束旁瓣级。例如，对于均匀线阵来讲，使用Dolph-Chebyshev加权可以得到给定主瓣宽度条件下最低的旁瓣级;Taylor和Villeneuve加权可以得到第一旁瓣为期望值且其他旁瓣逐渐衰减的波束图。然而，这些方法往往仅适用于标准线阵，不能直接应用于类似圆柱阵这样的阵形。利用相位模式激励方法可以很好解决上述问题［9，11］。

假定仿真条件同上，但这里要求基阵的旁瓣级低于－20 dB。根据式(9)，首先在水平方向上利用相位模式激励方法对每个圆阵进行Villeneuve加权，然后再在垂直方向上对每个圆阵的输出进行Dolph-Chebyshev加权，最终的合成波束图如图5所示。

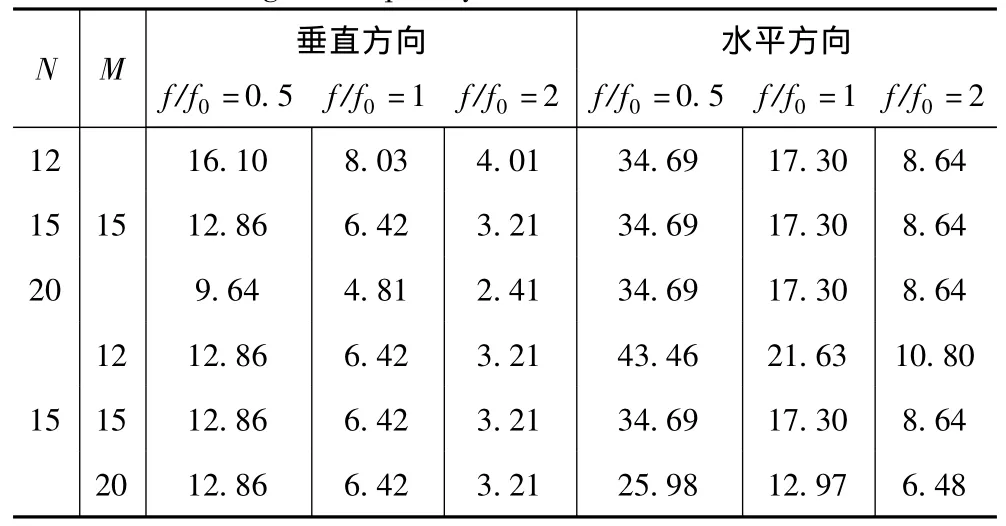
表1 波束宽度随阵元数和信号频率的变化关系Tab.1 The relationship among beam width，element number and signal frequency

表2 旁瓣级随阵元数和信号频率的变化关系Tab.2 The relationship among sidelobe level，element number and signal frequency

图5 加权圆柱形基阵波束方向图Fig.5 Beam pattern of cylindrical array with weights

图6和图7分别给出了波束图在θ=90°和φ=0°的切面图。从图中可以看出，通过对水平方向和垂直方向进行加权以后，波束图的旁瓣级得到明显降低，达到了所期望的－20 dB。在垂直方向上，得到了恒定的旁瓣，而在水平方向上，也可以得到与直线阵相似的衰减旁瓣。当然，旁瓣性能的改善必然会带来主瓣波束宽度的增加。通过比较图4与图5中可知，水平方向上波束宽度由原来的17°变为24°，而垂直方向则由原来的8°变为9°。所以，在实际应用时，应该综合考虑对波束宽度和旁瓣级的要求，设计合适的加权函数，得到波束宽度和旁瓣级综合最优的结果。

3 结语

本文从舰船辐射噪声测量的角度出发，以圆柱形基阵作为研究对象，对其指向性进行仿真估计并与直线阵和平面阵作对比，分析了柱形阵的性能及其优缺点。使用圆柱形基阵进行辐射噪声测量可以提高测量增益，能在空间360°范围内进行波束扫描，消除空间模糊，克服直线阵和平面阵等测量方式的许多弊端。对基阵波束图的性能参数如波束宽度、旁瓣级进行分析，并给出旁瓣控制波束图，使基阵能达到良好的性能。由于圆柱形基阵参与波束形成的阵元数目众多，其信号处理方法也极其复杂，实际应用中也会遇到更多的问题。因此，研究不同应用条件下的波束优化设计方法，是今后需要进一步开展的工作。

［1］陈守虎，等.使用垂直阵列测量舰船辐射噪声［J］.声学技术，2007，26(5):181 －182.CHEN Shou-hu，et al.Measurement of radiated ship noise with a vertical array［J］.Technical Acoustics，2007，26(5):181－182.

［2］杨德森，等.低噪声水下目标辐射噪声测量的新方法研究［A］.中国声学学会2001年青年学术会议［CYCA'01］论文集［C］，2001.245 －247.YANG De-sen，et al.A new method to measure the radiated noise of low noise level submerged targets［A］.China Institute of Acoustics 2001 Youth Conference Proceedings［CYCA'01］.2001.245 －247.

［3］GEE T，PEPE K.Compesation for missing sensors in a realtime measurment beamformer system［A］.IEEE OCEANS，1998.351 －357.

［4］DENOLFO P，HARRISON M，THOMSON H，et al.South TOTO acoustic measurement facility(STAFAC)in-water systems installation autec andros island，bahamas［A］.IEEE OCEANS，2008.1 －16.

［5］王之程，等.舰船噪声测量与分析［M］.北京:国防工业出版社，2004.WANG Zhi-cheng，et al.Warship noise measuring and analyzing［M］.Beijing:National Defense Industry Press，2004.

［6］NUTTALL A H，CRAY B A.Efficient calculation of directivity indices for certain three-dimensional arrays［D］.NUWC-NPT Technical Report，1996，7 －26.

［7］WAITE A D.实用声呐工程［M］.王德石，等译，北京:电子工业出版社，2004.WAITE A D.SonarforPractisingEngineers［M］.Translated by WANG De-shi.Beijing:Publishing House of Electronics Industry，2004.

［8］WIRTH W D.Radar techniques using array antennas［M］.The institution of Electrical Engineers，London，United Kingdom，2001.

［9］Van.TREES H L.最优阵列处理技术［M］.汤俊，等译，北京:清华大学出版社，2008.Van.TREES H L.Optimum Array Processing［M］.Translated by TANG Jun，Beijing:Tsinghua University Press，2008.

［10］周福洪.水声换能器及基阵［M］.北京:国防工业出版社，1984.ZHOU Fu-hong.Underwater acoustic transducer and array［M］.Beijing:National Defense Industry Press，1984.

［11］DAVIES D E N.A transformation between the phasing techniques required for linear and circular aerial arrays［C］.Proceedings IEE，1965，112:2041－2045.