深埋爆炸波传播规律及边界条件转换分析
2012-08-20范伟东
李 杰 胡 啸 范伟东
(1.解放军理工大学工程兵工程学院,江苏 南京 210007; 2.空军后勤部机场营房部,北京 100720;3.沈阳军区空军后勤部机场营房处,辽宁 沈阳 110015)
0 引言
随着较浅部能源的大量开采,越来越多的矿井正在向深部转移,另外随着钻地武器的发展,各国的重要地下战略工程也在逐渐向深部转移。这些都要求对深部岩石中爆炸引起的应力、变形及其他运动参数给出比较准确的评估。
由于岩石中爆炸的瞬时性和复杂性使其研究十分困难,大多数研究表明[1-3],炸药在地下爆炸时,根据周围介质破坏的特点,由里及外依次可以分为爆炸腔、破碎区、径向裂缝区和弹性区。根据爆炸的等效荷载理论,把浅埋爆炸的整个非弹性破坏区看成震动源,利用当前较为成熟的弹性波理论,可以大大地降低难度,对于爆炸远区的研究具有重要的意义。
爆炸等效荷载的表示形式通常有两种[4]:第一种由空腔表面的径向粒子速度来描述;第二种由空腔表面径向正应力来描述。在岩石介质的地下爆炸试验研究过程中,因为准确应力场数据的测量较为困难,大部分的测量数据为速度场数据,而在进行有限元等数值分析时,将球腔内速度加载转换为压力加载可降低研究难度,因而建立一个相对准确的应力与速度之间的转换关系是十分必要的。经典的弹性波理论中,应力场和速度场存在简单的线性转换关系σ=ρCv[5]。但这种关系的成立只是建立在一维平面波的假设上,将其应用于球面波,无疑会产生很大的误差。
本文在爆炸的等效荷载理论以及弹性波理论的基础上,详细探讨了深埋爆炸波的传播规律,并通过计算建立了通用的应力与速度转换关系。
1 震源简化模型
深埋地下爆炸由于炸药埋置深度很大,可以不考虑地表面对地下自由场中波传播的影响,把问题看成无限介质中的球对称问题进行研究。根据爆炸等效荷载理论可以将整个非弹性区看成爆炸的震动源,简化后的爆炸地震波传播如图1所示。
震源为以O为球心,R0为半径的球形空腔。边界上的等效荷载可以用空腔表面的径向粒子速度vR=vR(t)或者空腔表面径向正应力σR=σR(t)来描述。设弹性半空间介质的材料特性用密度ρ、泊松比v、拉梅常数λ和μ表示,纵波速度用Cp,横波速度用Cs表示。
在t=0时刻球形空腔表面产生弹性压缩波,震源周围介质质点的一维径向运动线性微分方程,可用球坐标r,θ,φ表示为[6]:
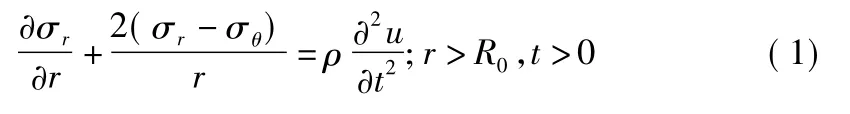
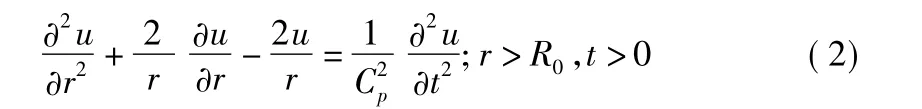
2 边界条件转换
在t=0初始时刻球形弹性压缩波就开始激活周围的介质,这就引起下列边界条件。
2.1 速度边界条件
对于第一种边界等效荷载,设其具体如下式:


对式(4)求时间t的导数,可以得到速度的表达式:
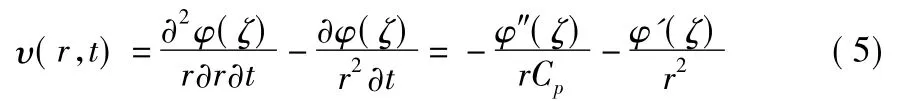
当r=R0时,有ζ=t,再将式(5)代入边界条件式(3)有:
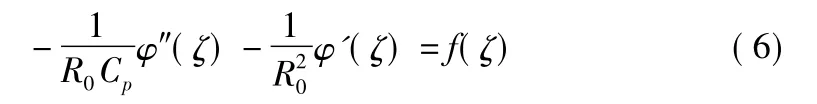
初始条件为φ″(0)=0,φ′(0)=0时,势函数可以用卷积积分表示成:

2.2 应力边界条件
对于第二类扰动形式,类似于式(3),在半径r=R0的球面上给出了正应力型边界条件:

在这种情况下,利用式(4)代入式(1)中 σr,σθ,σφ的表达式可以得到:


然后可以得到:

2.3 边界条件的相互转换
因为不同边界条件对应的是相同的运动场,所以令式(7)和式(11)的右边相等,有:

等式两边分别对其进行Laplace变换有:
把式(14)代入式(13),化简后有:
运用留数定理进行计算有[7]:

再设:
根据卷积定理有:
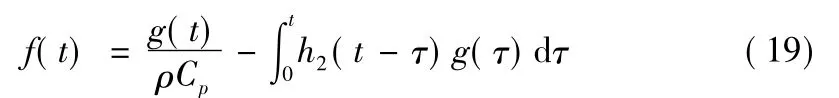
由式(18)和式(19)即可完成应力边界条件到速度边界条件的转换。
同理也可以得到由速度边界条件到应力边界条件的转换:

设:
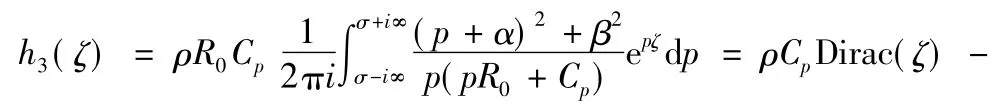

再设:
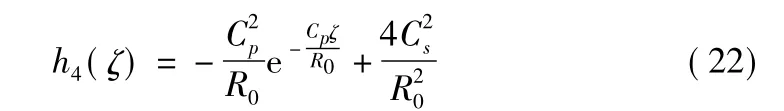
根据卷积定理有:

由式(22)和式(23)即可完成应力边界条件到速度边界条件的转换。
2.4 计算实例
以正弦指数衰减速度边界条件和双指数应力边界条件为例进行计算,计算参数如表1所示。

表1 计算参数
1)正弦指数衰减速度边界条件。
正弦指数衰减速度边界条件的表达式为[8]:

其中,υ0为速度量纲常数;α为衰减系数;ω为振动频率。取υ0=10 m/s,α =1 600,ω =5 000,则边界条件图形如图2 所示。

图1 深埋爆炸震源简化模型

图2 正弦指数衰减速度边界条件
把式(24)代入式(23)可以得到其所对应的应力边界条件如图3所示。
由上面的计算可以看出,对应于正弦指数衰减的速度边界条件,其应力的波动周期与速度波动周期相等。随着时间的发展,应力趋于一极限值,考虑到爆炸近区的特点,可以理解为残余应力[9]。与平面波阵面上的关系式σ=ρCpυ比较,转换后边界最大应力要比σ=ρCpυ计算得出的大30%左右。
2)双指数应力边界条件。取应力边界条件为双指数函数和形式,双指数函数[8]的数学表达式如下:

其中,k为峰值修正系数;p0为脉冲峰值;a和b的值影响脉冲峰值、前沿、半宽等参数。
取a=1 279,b=12 792,k=1.435时可以得到一个升压时间为0.000 2 s、峰值压力为p0=100 MPa的脉冲荷载。其图形如图4所示。

图3 应力边界条件

图4 双指数压力荷载
将式(25)代入式(19)得到双指数应力边界条件对应的速度边界条件波形如图5所示。
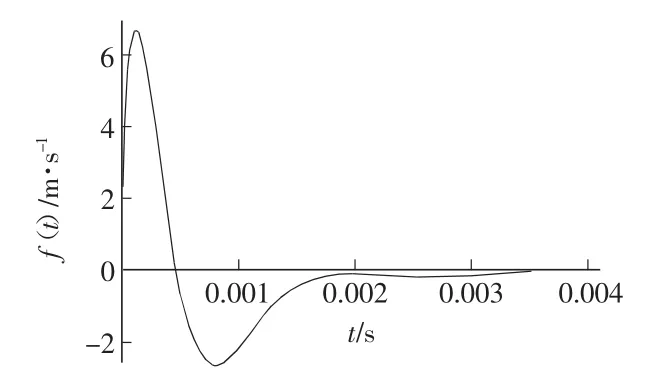
图5 速度边界条件
由图5可以看出,速度条件的升压时间小于应力条件,与平面波阵面上的关系式σ=ρCpυ比较,转换后边界最大速度要小20%左右。
由此可以得出,与平面波中应力和速度的线性关系相比较,相同应力边界条件下球面波上的质点的速度要小,分析式(19),式(23)可以看出影响这种差异大小的主要因素是波的传播距离和介质中波的传播速度。
3 深埋爆炸波的传播规律
式(9)用来描述应力随距离的变化,这种变化比流体中的应力变化要复杂,公式中的第二项以及第三项用来表述介质的抗剪能力(μ≠0)。如果μ=0,即Cs=0,可得到对应于流体的解:

式(9)的第一项描述在r→∞时应力的渐进行为,如果引进非平稳波的波长概念,即λ=CpT(T为脉冲的特征时间),那么式(9)的第一项以很好的精度描述在r≫λ时应力随时间的变化。
如果g(t)=σ0H(t),H(t)为阶跃函数,则式(11)最终表达式为:

从式(27)中可以看到,在固定位置存在着阻尼振荡,显示了球面波与平面波的截然不同,球面波的情形场变量服从至少是r-1量级的几何衰减。
此时,对于r≫λ条件,速度的近似表达式为:
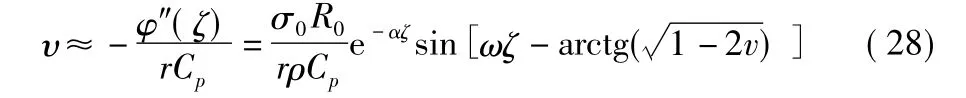
分析这最后的关系式表明:介质的空间(径向)运动具有使振动衰减的特点。振幅的衰减参数为振动的有条件周期等于,它与土壤的性质和震源的半径有关。
可见,剪应力τmax(r/R0)在震源r=R0和弹性波阵r=R0+Cpt的区域内,是坐标r/R0的单调递减函数。在震源表面(r=R0)上达到最大值,而在波阵面前达到最小值。波阵上各点处的振幅,由于弹性压缩波的传播有一个突降值[6],因此剪切力的振幅也将有一个突变。
图7计算给出了观察点r/R0=1.1和1.5处对应于式(17)相对环向应力随时间 t/t0变化的历程。在介质运动的初始阶段,环向应力是拉应力(>0),然后拉应力变成压应力(<0)。拉应力可能引起(在许多情况下都会引起)径向裂纹破坏。当t无限增加时,趋近于静力解。
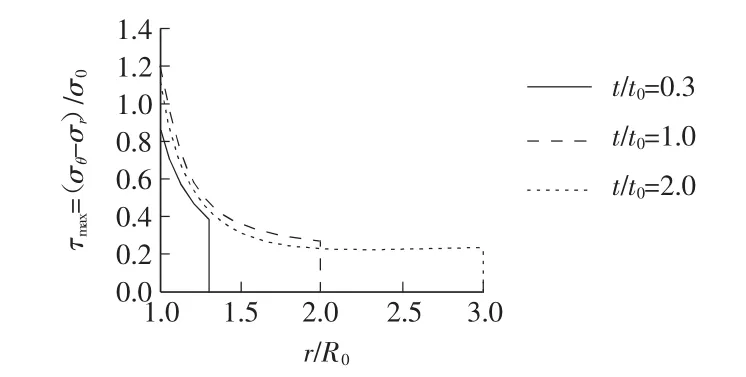
图6 最大剪应力沿半径的分布

图7 环向正应力的时程曲线
如果在球形震源r=r0表面上作用的是静荷载σ0,可以得到无穷大弹性介质中边值问题的精确解析解:

可见静力问题中环向应力σθ(r)总是拉应力,径向应力σr总是压应力(σr<0)。静应力的幅值随着远离震源而与一样衰减,位移场则与一样衰减,应力与静态作用力源周围介质的参数无关。
4 结语
以弹性空腔膨胀为研究对象,利用速度和应力两种边界条件下运动场势函数相等的原理,建立了球面波运动场中速度场与应力场的转换关系。结果表明:
1)不同于平面波中应力和速度的线性关系,球面波中应力与速度转换关系要复杂的多,相同应力条件下,球面波上的质点的速度要小,影响这种差异大小的主要因素是波的传播距离和介质中波的传播速度。2)通过对阶跃压力荷载作用下应力场的衰减规律研究发现,球面波的情形场变量随着远离震源服从至少是γ-1量级的几何衰减。3)介质的径向运动具有使振动衰减的特点。振幅的衰减参数和振动的有条件周期与土壤的性质和震源的半径有关。4)剪应力在震源γ=R0和弹性波阵r=R0+Cpt的区域内是坐标r/R0的单调递减函数,在震源表面上达到最大值。波阵上各点处的振幅,由于弹性压缩波的传播有一个突降值,因此剪切力的振幅也将有一个突变。5)在介质运动的初始阶段,环向应力是拉应力,然后拉应力变成压应力。拉应力可能引起(在许多情况下都会引起)径向裂纹破坏。当t无限增加时,环向应力趋近于静力解。6)静力问题中环向应力总是拉应力,径向应力总是压应力。静应力的幅值随着远离震源而与一样衰减,位移场则与一样衰减,应力与静态作用力源周围介质的参数无关。
[1] 葛 涛,吴华杰,陶剑青.岩石中爆炸破碎区边界参数研究[J].爆破,2005,22(3):5-8.
[2] 钮 强.岩石爆破机理[M].沈阳:东北工学院出版社,1990.
[3] В.С.Никифровский,Е.И Шемякин Динамическое разрушен-ие тведого тела[M].Новосибирск:Наука,1979.
[4] 丁 桦,郑敏哲.爆破震动等效载荷模型[J].中国科学(E辑),2003,33(1):82-90.
[5] 王礼立.应力波基础[M].北京:国防工业出版社,2005.
[6] 阿肯巴赫.弹性固体中波的传播[M].徐植信,译.上海:同济大学出版社,1992.
[7] 管 平,计国君,黄 骏.数学物理方法[M].北京:高等教育出版社,2001:39-45.
[8] 唐 廷,尤 峰,葛 涛,等.爆炸荷载简化形式对弹性区应力场的影响[J].爆破,2007,24(2):7-10.
[9] J·亨利奇.爆炸动力学及其应用[M].熊建国,译.北京:科学出版社,1987.
