基于WIMS和MCNP耦合程序的医院中子照射器I型堆燃耗计算

郭和伟，江新标，赵柱民，陈立新，张信一，周永茂

(1.西北核技术研究所，西安 710024;2.中国核工业集团中原对外工程有很公司，北京 100191)

1 前言

要保证医院中子照射器I型堆10年不换料连续运行，燃耗计算十分重要。MCNP程序可求解任意三维复杂几何系统内的粒子输运问题，具有真实模拟粒子轨迹的特点，具有非常强大的几何处理能力，但其不能直接进行燃耗计算。为此，文章利用MCNP的多群计算功能和WIMS栅元程序耦合，实现了燃耗计算，并利用此方法计算了I型堆的燃耗。该程序的主要思路是:首先将能量分群，把对连续能量的中子跟踪问题转变为对能群的中子跟踪问题;然后，参考积分输运理论，用栅元程序WIMS对堆芯中的基本栅元进行均匀化处理，并求出考虑非均匀效应后的均匀化群常数;最后，应用栅元程序WIMS进行栅元燃耗计算，求出栅元群常数与燃耗的关系，提供给MCNP进行计算，完成堆芯的燃耗计算。

2 临界－燃耗耦合程序的研制

2.1 多群临界计算

MCNP程序多群功能求解多群中子输运方程[1]形式为:

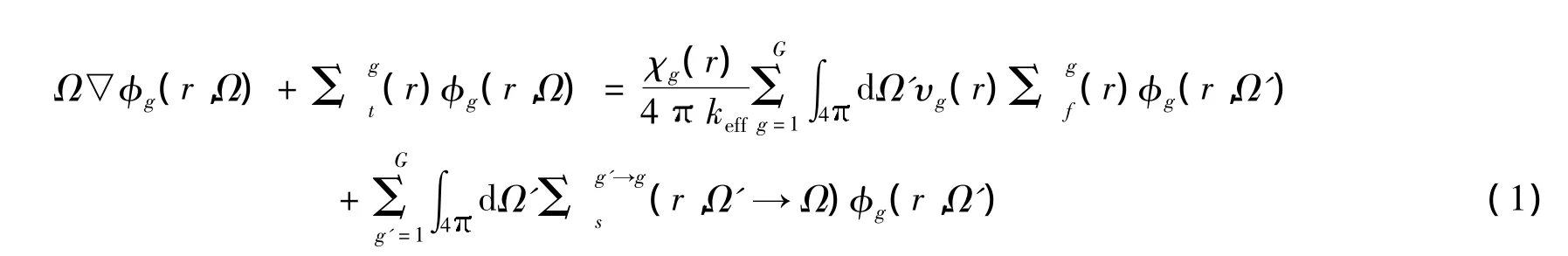
式(1)中χg为g群中子裂变向量谱。通过求解此方程，即可求得系统的有效增值系数keff。

2.2 燃耗计算

计算燃耗时，首先用WIMS程序计算出每根燃料棒、不同燃耗值对应的宏观中子截面(截面考虑了共振自屏、互屏及温度效应)，然后由接口程序完成截面的转化，生成MCNP用的多群截面。计算流程如图1所示。

耦合程序计算燃耗的基本过程如下:a.在keff及中子通量密度收敛后，利用该中子通量密度计算每根燃料元件的功率，进而计算其燃耗;b.由计算出的燃料元件功率及燃耗，利用WIMS计算出新的多群截面，经过接口程序转化后，将此截面替代上一步耦合程序中的多群截面，再次计算keff及中子通量密度，如此循环，直到满足结束条件(一般为keff=1)。

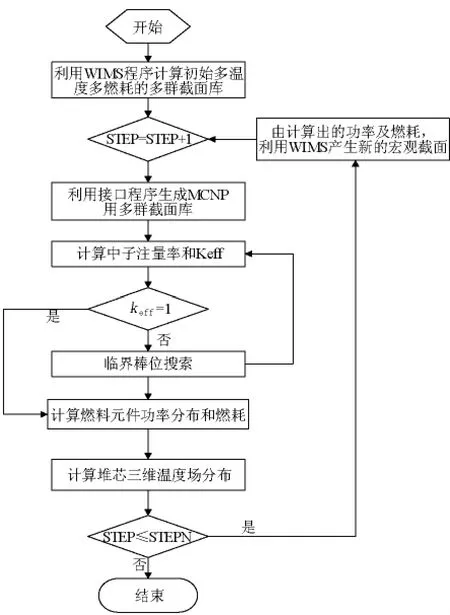
图1 WIMS与MCNP耦合计算流程Fig.1 The coupled calculated flow of WIMS and MCNP

其中第i根燃料元件的功率Pi和当前燃耗增量ΔBU(i)的值由下式计算[2]:

式(2)～(4)中 Σf，g(i)为第i根燃料元件、第g群裂变截面;φg(i)为第i根燃料元件的中子通量密度;κ为每次裂变所放出的能量，MeV;Pv为堆芯总功率;N为堆芯中总的燃料元件个数;Δt为燃耗步长，d;mi为第i根燃料元件的初始铀装量，t。

3 临界－燃耗耦合程序的验证

3.1 燃料栅元及组件问题

主要验证不同方法在不同燃耗下单棒和组件的无限增值系数 K∞随燃耗的变化情况。其中U －ZrH1.6燃料芯体铀含量为 12%(重量)，235U 富集度为19.75%，密度为6.1792 g·cm－3。每块燃料芯体外径为 36.1 mm，内径为 4.6 mm，长度为130 mm。包壳管采用0Crl8Ni11Ti不锈钢，内径为36.2 mm，壁厚0.5 mm，长614 mm。数据验算主要采用连续点 MNCP、WIMS和 MCNP耦合计算及ORIGEN2以及MCNP耦合计算3种不同方法，计算了无限增值系数的变化。单棒和组件模型如图2、图3所示，比对结果如图4、图5所示。

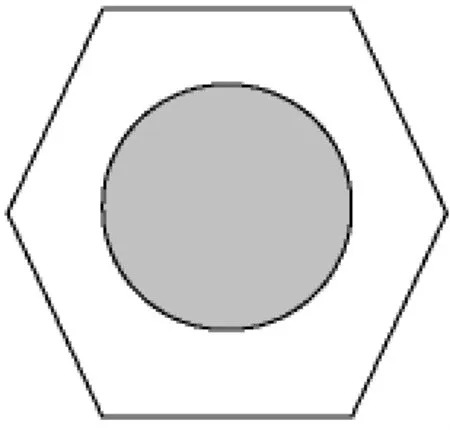
图2 单棒栅元模型Fig.2 The model of fuel cell

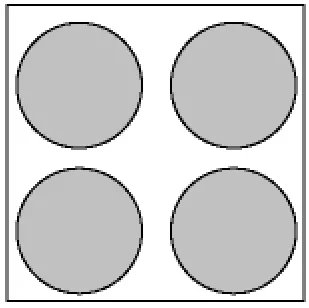
图3 组件模型Fig.3 The model of fuel assembly

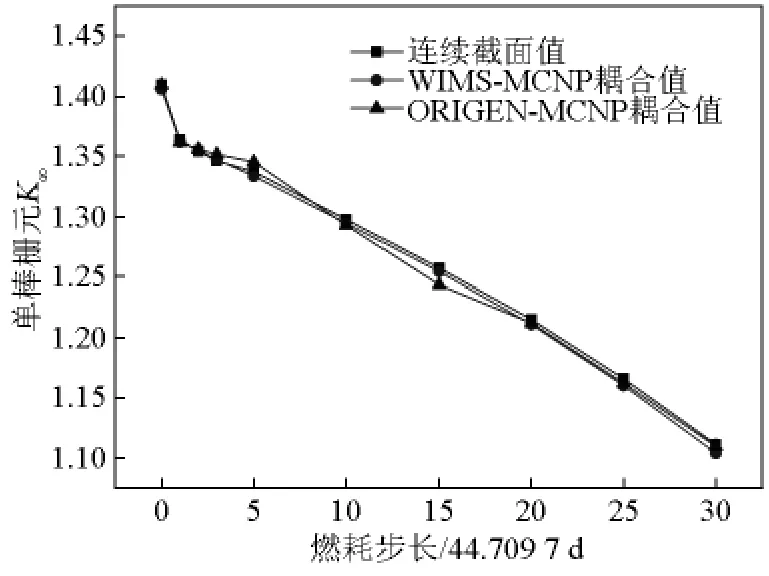
图4 单棒无限增值系数的对比Fig.4 Comparison of infinite multiplication factor for fuel cell

如图4、图5所示，在不同燃耗下的计算结果表明，采用3种不同方法结果符合一致，计算偏差在0.5%左右。验证了WIMS以及MCNP耦合计算方法是正确可靠的。

3.2 实际堆验证

图5 组件无限增值系数的对比Fig.5 Comparison of infinite multiplication factor for fuel assembly

利用西安脉冲堆的燃耗实验测量结果[3]对此耦合程序进行了验证。西安脉冲堆堆芯呈正三角形排列，栅距为43 mm，9圈共211个孔位，中心7个孔为中央垂直孔道占据，控制棒占据6个孔位，燃料元件占据105个孔位，中子源占1个孔位，跑兔辐照管占2个孔位，其余为石墨元件。利用此耦合程序，进行了堆芯燃料棒的燃耗计算，文章计算了满功率运行15天后(简称15EFPD)，D5和G14燃料棒的燃耗，由于燃料棒轴向功率分布的不均匀性，会导致燃料棒不同高度处燃料成分的不同，因此对D5和G14两根燃料棒进行了轴向分层，对不同高度处235U的含量进行了计算，并与实验值和ORIGEN2以及MCNP的耦合程序计算值进行了对比，计算结果如图6和图7所示。

图6 D5棒燃耗分析Fig.6 Burnup analysis for D5 fuel cell

从图6和图7比对结果可以看出，文章开发的WIMS和 MCNP耦合方法计算值与 ORIGEN2和MCNP耦合方法计算值符合较好。对于 D5棒，WIMS和MCNP耦合燃耗计算值和实验值的偏差不超过20%;对于G14棒来说，其偏差在5%左右，而实验测量值有20%的不确定度，计算分析值和实验值在误差分析范围内一致，这也证明文章所开发的临界－燃耗耦合方法是可行的。

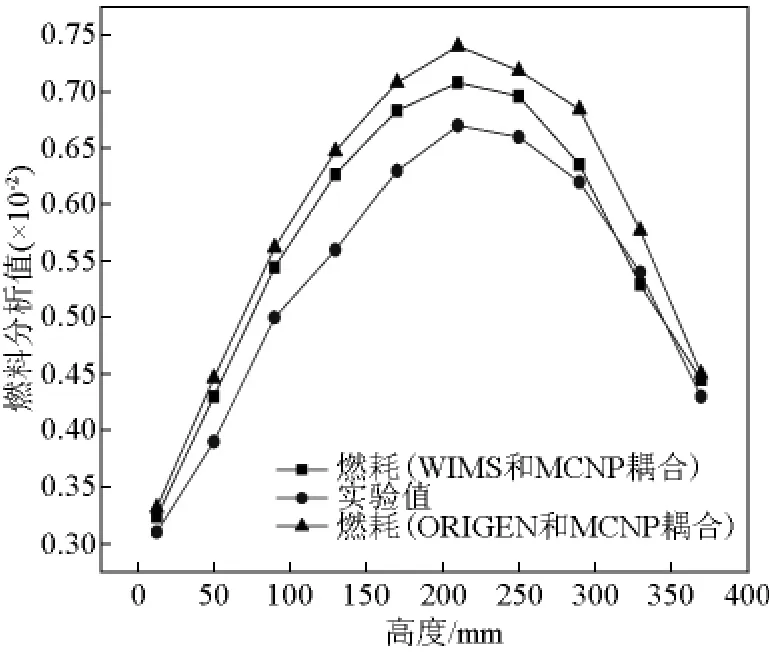
图7 G14棒燃耗分析Fig.7 Burnup analysis for G14 fuel cell

4 医院中子照射器I型堆燃耗计算

医院中子照射器I型堆堆芯由中心控制棒栅元(净堆计算时该栅元为水)和10圈燃料栅元组成，每圈燃料栅格孔在该圈内均匀排布，燃料元件由上下栅板定位，组成栅位，其中有燃料栅位，Zr－4连接杆栅位，燃料元件采用烧结UO2燃料芯体，芯体有一定高度活性区;包壳采用Zr－4;芯体与包壳管之间为氦气;芯体上下端塞采用Zr－4材料，上下端塞有一定厚度，上端塞与燃料芯体之间有气隙;中心控制棒栅元外围有Zr－4导管。堆芯共有10圈燃料元件，计为A～J。

文章应用WIMS－MCNP燃耗耦合程序，计算了医院中子照射器I型堆30 kW功率运行，不换料情况下连续运行10年(运行模式:8 h/d、5天/周、52周/年、堆芯功率30 kW)燃料的燃耗情况，10年等效运行866.7等效天。

计算中取40等效天为一个燃耗步长，计算了堆芯轴向分层燃料芯体的燃耗情况，由于堆芯燃料栅元在各圈内均匀分布，其轴向功率分布在各圈内基本相似，因此，文章在A～J圈分别选择A1、B1、C1、D1、E1、F1、G1、H1、I1、J1 燃料芯体来计算各圈燃料芯体的燃耗分布，主要计算235U的含量变化。计算采用WIMS－MCNP耦合方法和ORIGEN2－MCNP耦合方法进行对比。分别计算了40等效天和866.7等效天的燃耗情况。

运行40等效天时，选取了B1和H1两根燃料棒进行了燃耗计算，结果如图8、图9所示。运行866.7等效天(10年)时，B1和H1两根燃料棒燃耗的变化情况结果如图10、图11所示。

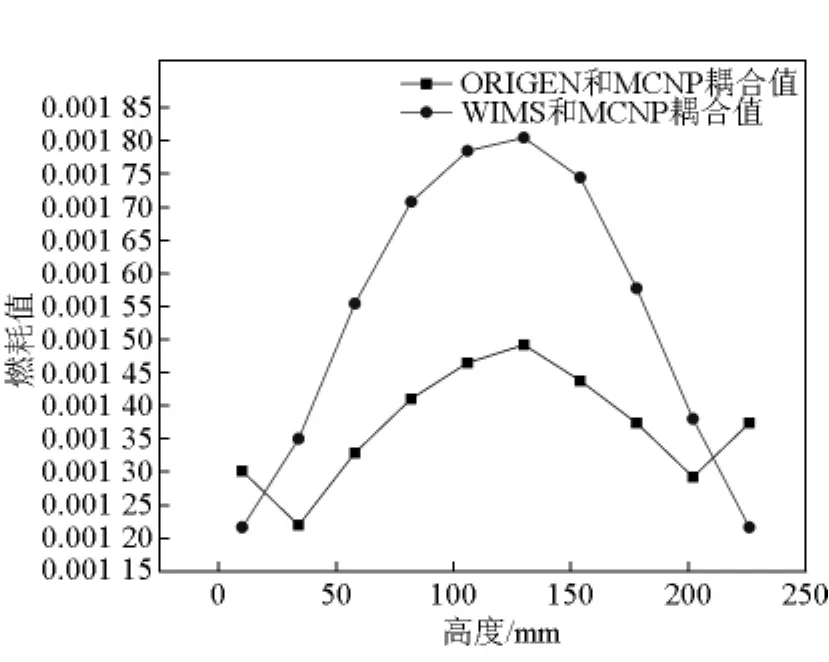
图8 B1棒燃耗分析Fig.8 Burnup analysis for B1 fuel cell

图9 H1棒燃耗分析Fig.9 Burnup analysis for H1 fuel cell

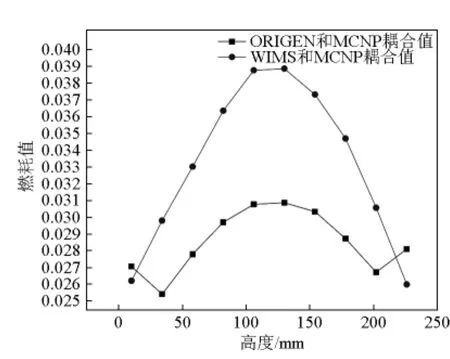
图10 B1棒燃耗分析Fig.10 Burnup analysis for B1 fuel cell

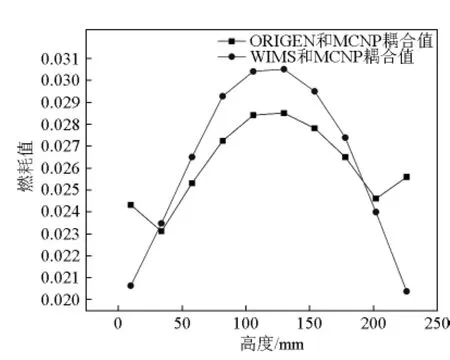
图11 H1棒燃耗分析Fig.11 Burnup analysis for H1 fuel cell

从图8～图11可知，文章耦合程序对医院中子照射器 I型堆 B1和 H1两根燃料棒计算值比ORIGEN2和MCNP耦合计算值偏大，且轴向两端的反射层效果没有体现出来，这是文章耦合程序计算的不足之处，但是总体趋势符合一致。

5 结语

文章建立了基于WIMS和MCNP的燃耗耦合计算方法，并利用栅元及组件问题和西安脉冲堆的燃耗实验比对，验证了此耦合程序的可行性。最后应用此耦合程序计算了医院中子照射器I型堆堆芯燃料的燃耗情况，并与ORIGEN2和MCNP耦合程序计算结果进行了对比分析，从比对结果可以看出，耦合计算方法值比ORIGEN2和MCNP耦合值普遍偏大，且轴向的上层和下层的反射层效果没有体现出来，使结果造成了一定误差，但是总体上趋势是一致的，可以作为燃耗分析的一种依据。

[1] 谢仲生，邓 力.中子输运理论数值计算方法[M] .西安:西北工业大学出版社，2005:48－54.

[2] 李 树.堆芯燃耗分析系统及其应用[D] .西安:西安交通大学核能与热能工程系，2000.

[3] 张文首，阿景烨，陈 达，等.西安脉冲堆燃料元件燃耗无损实验测量[J] .核动力工程，2009，30(3):30 －34.