用相对速度解决圆心是动点的圆周运动的动力学问题
2012-08-16赵灿冬
赵灿冬
(靖江高级中学 江苏 泰州 214500)
【例1】如图1所示,质量为M的光滑半圆形凹槽放在光滑水平面上,凹槽的半径为R,质量为m的小球从凹槽的左侧最高点由静止释放,求当小球滑至凹槽的最低点时,小球对凹槽的压力.

图1
解析:根据动量守恒定律的相关知识可知,小球的运动轨迹不是圆,但小球相对于半圆形凹槽的运动是一个圆.所以本题可以以半圆形凹槽为参考系来解决问题.
首先计算小球运动到最低点时,小球和半圆形凹槽的速度.
当小球滚到凹槽的最低点时,根据水平方向动量守恒
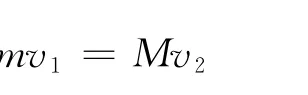
根据机械能守恒

当小球滚到凹槽的最低时

式中v相是小球相对于半圆凹槽的相对速度.答案是肯定的,但疑问是有的.
为什么可以用相对速度来计算?
本题在求解的过程中,有一个问题没有说清:相对于半圆形凹槽做圆周运动就一定可以这样列式求解吗?回答是否定的,因为在本题中还有一个隐藏的条件:当小球在最低点时,圆弧槽的加速度为零.
分析半圆形凹槽的受力可知,在水平方向半圆形凹槽不受力的作用,所以其加速度为零.而小球相对于半圆形凹槽做圆周运动,此时,相对于半圆形凹槽,其相对加速度
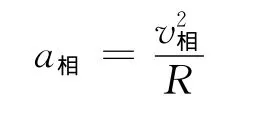
所以,球对地加速度
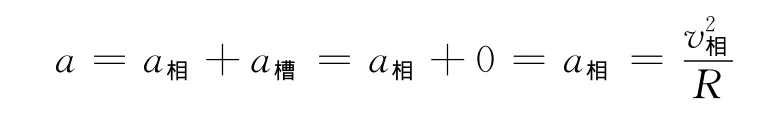
因此本题可以用相对速度计算向心力来求解的关键是半圆形凹槽的加速度为零,而不是选择了半圆形凹槽为参考系.实际上,由于在整个过程中,半圆形凹槽做变速运动,不是真正良好的惯性系.本题不需要选择其为参考系,只要根据运动的相对性和加速度的牵连关系求出小球的对地加速度即可求解.
有些情况下,物体可以相对于一个有加速度的另一物体做圆周运动,这时也可以根据牵连关系求解.
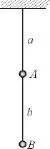
图2
【例2】如图2所示,用长为l的轻绳a和b竖直悬挂质量均为m的小球A和B,某时刻,突然给球A一个水平向左的冲量I后,求此时绳a和绳b的张力.
错解:因为B球相对于A球做圆周运动,所以B球的加速度为

分析B球的受力,根据牛顿第二定律

解出

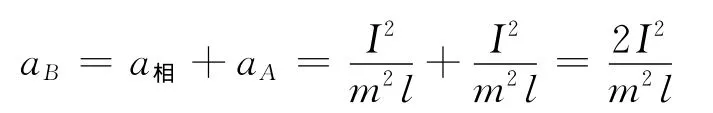
分析球B的受力,根据牛顿第二定律

解出

再对球A受力分析,根据牛顿第二定律

解出
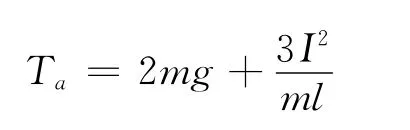
2005年江苏高考的最后一道题在参考答案中就注意到了这一问题,并给出了说明.
【例3】如图3所示,三个质量均为m的弹性小球用两根长均为L的轻绳连成一条直线而静止在光滑水平面上.现给中间的小球B一个初速度v0,方向与绳垂直.小球相互碰撞时无机械能损失,轻绳不可伸长.求当三个小球处在同一直线上时,绳中的拉力F的大小.

图3
解析:当三个小球再次处在同一直线上时,则由动量守恒定律和机械能守恒定律,得

以后三球还会处于同一直线,三球的速度回复到初始状态

小球A和C均以半径L绕小球B做圆周运动,在两种情况下,当三个小球处在同一直线上时,以小球B为参考系(小球B的加速度为零,为惯性参考系),小球A(C)相对于小球B的速度均为

所以,此时绳中拉力大小为

本题特别强调了小球B的加速度为零这一特殊条件.
用这一方法可以求例1中小球在任意位置的速度吗?回答是肯定的,只是比较繁.

图4
例1解法2:设小球在某时刻和球心的连线与水平方向夹角为θ,如图4(a)所示.
此时,半圆形凹槽的速度大小为vM,小球的速度大小为vm,小球速度的水平分量大小为vmx,竖直分量大小为vmy,如图4(b).
根据小球相对于半圆形凹槽的速度沿圆弧的切线方向,可得

根据水平方向动量守恒

根据机械能守恒

可得

由图4(b)可知
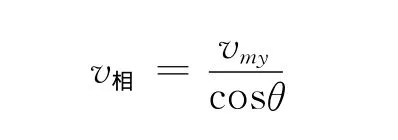
解得
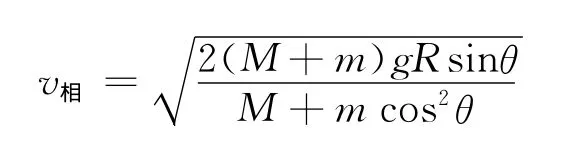
设半圆形凹槽对小球的作用力为N,则半圆形凹槽的加速度为
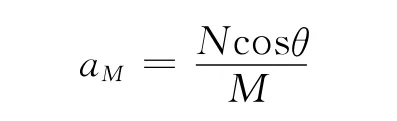
沿半径方向的分量为

所以小球对地沿半径方向的加速度为

分析小球的受力,在沿半径方向,根据牛顿第二定律得

解得

用相对速度解决动圆心的圆周运动问题拓宽了解题的思路,但是要注意分清圆心的加速度,这一点是关键.
