平顶 －高斯光束通过圆形与三角形围成孔的衍射＊

张亚萍 顾菊观 杨 平 陈小燕 沈曼辰

（湖州师范学院理学院 浙江 湖州 313000）

1 引言

Cori提出的一种新的平顶 －高斯光束模型［1］，其光强特点为均匀的平顶分布，在激光光学中得到了广泛的研究与应用.目前，国内外主要研究平顶－高斯光束相对焦移、M2因子、K参数以及在圆孔、矩孔硬边光阑等中的衍射特性［2～5］，而对围成孔硬边光阑的衍射研究很少见，光束通过圆形与三角形围成孔的研究在文献中还未曾见过.基于这些情况，文中从其表达式出发，结合Collins公式和Matlab软件，研究并分析了平顶 －高斯光束通过圆形与三角形围成孔的硬边光阑光学系统的衍射特性.

2 平顶 －高斯光束通过带有圆形与三角形围成孔的硬边光阑光学系统的传输

在直角坐标下，三维平顶 －高斯光束的场分布在入射平面（x1O1y1）处可用下式表示［5，6］

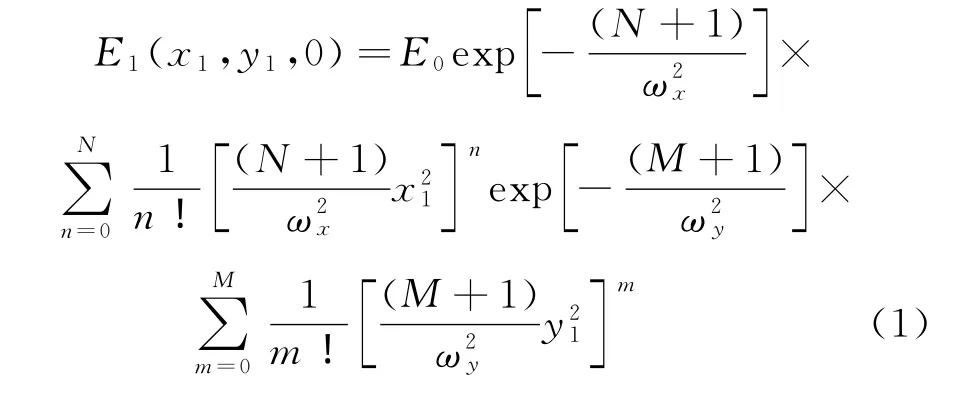
式中E0是振幅；N，M分别是平顶 －高斯光束在x，y方向阶数 （N＝0，1，… 及M＝0，1，…）；ωx，ωy分别为平顶 －高斯光束在x，y方向的束腰宽度.

对于三维的情况，近轴ABCD光学系统的Collins衍射积分公式为［6～8］

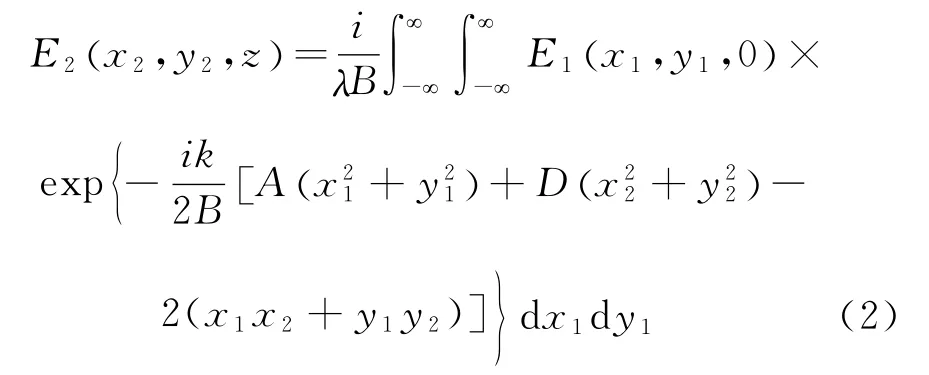
式中略去了exp（－ikz）.

将式（1）代入式（2），可得三维平顶 －高斯光束的衍射积分公式为

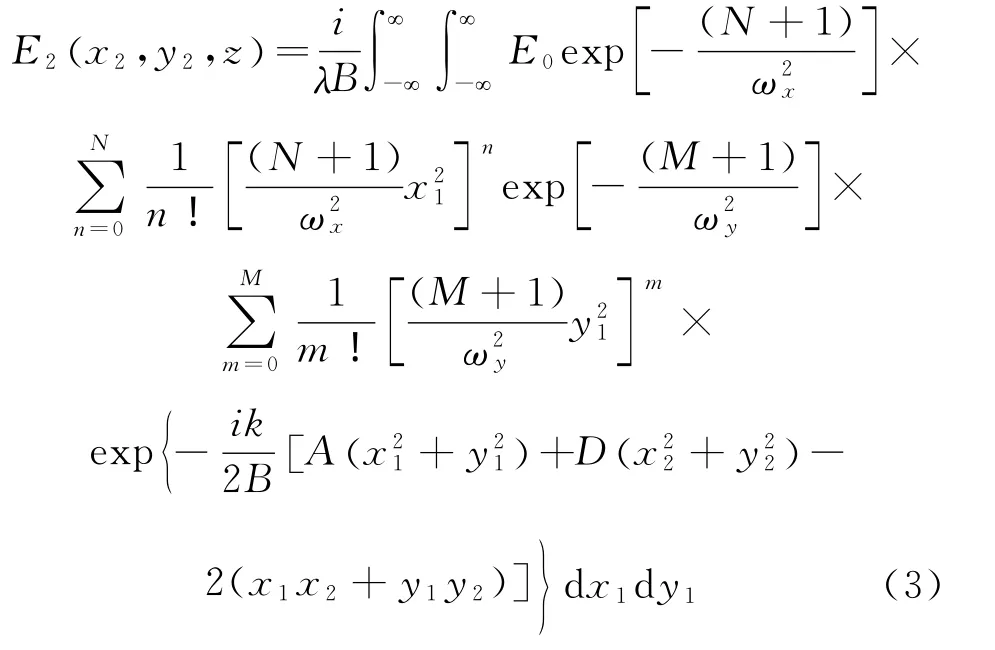
因三角形的非对称性，近似解析的传输公式无法用复高斯函数展开或其他方法求得，故利用Matlab中辛普森积分方法，直接对式（3）进行数值积分［9］.

3 数值模拟分析

平顶 －高斯光束在阶数大于10以后，光强分布图样变化不大，其光强顶部呈平面状，光强分布如图1所示，故称为平顶 －高斯光束.在Matlab环境下，对式（3）进行数值积分模拟，模拟时假设束腰在孔面上，衍射屏为圆形与三角形围成孔，且圆心与三角形的外心重合，如图2.其中参数λ＝632.8nm，ωx＝ωy＝1mm，N＝10，M＝10［3，6］.

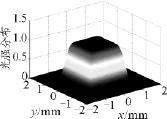
图1 N ＝10，M ＝10平顶 －高斯光束的光强分布

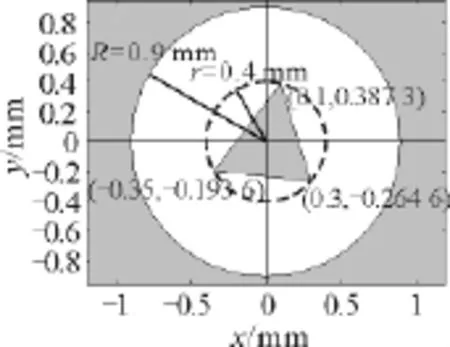
图2 圆形与三角形围成孔

3.1 衍射光强I与传输距离z的关系

图3对应于半径R＝0.9mm的圆形与三角形（外接圆为r＝0.4mm，0.6mm，0.8mm）围成孔，数值模拟平顶 －高斯光束通过围成孔后的自由传输情况.由图3知：

（1）3个孔的衍射结果在传输距离z较小时，震荡明显，即明暗变化显著，符合菲涅耳衍射特性.随传输距离z的增大，都存在菲涅耳衍射与夫琅禾费衍射转化，转化点后衍射特性与夫琅禾费衍射特性一致，即明暗震荡现象消失，一直保持亮斑；

（2）菲涅耳衍射与夫琅禾费衍射转换点随三角形外接圆半径增大（衍射孔径减小）而靠近衍射屏，即菲涅耳衍射区域缩小；

（3）衍射光强随三角形外接圆半径增大而减弱.

对于平顶 －高斯光束通过不同半径的圆形与三角形围成孔的自由传输特性，其数值模拟的方法及结果与上述类似.

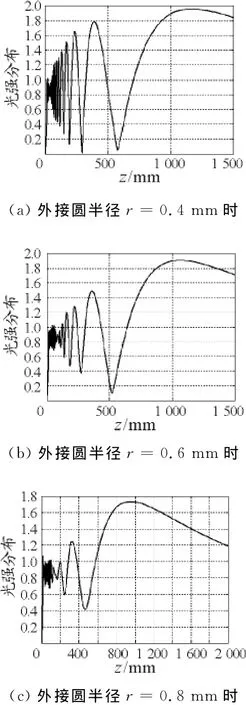
图3 圆形（R＝0.9mm）与外接圆半径不同的三角形围成孔的情况下，光强分布与传输距离的关系

3.2 衍射光强I与x和y的关系

图4对应于半径R＝0.9mm的圆与外接圆半径r＝0.8mm的三角形围成孔，数值模拟平顶 -高斯光束通过围成孔后的自由传输特性情况.

由图4知：

（1）图4（a）、（b）表示菲涅耳衍射区内传输距离z＝100mm，200mm的x，y轴方向上的衍射图样.由图4知，z＝100mm，200mm处的衍射图样变化明显；图4（c）、（d）表示夫琅禾费衍射区内z＝1 500 mm，2 000mm的衍射图样，衍射图样形状基本保持不变，光强变弱；以上两点分析结果与3.1结果相符，也与菲涅耳衍射与夫琅禾费衍射特点相符；

（2）菲涅耳衍射区z＝100mm，200mm的衍射有多峰现象，观察屏中心的亮斑与泊松亮斑相似［10］，夫琅禾费衍射区z＝1 500mm，2 000mm 的衍射只有单峰现象，传输距离z越远，中心处的衍射光强越弱；

（3）不同传输距离处，x，y轴方向上的菲涅耳衍射和夫琅禾费衍射图样都不具有对称性，这与围成孔的三角形在x，y轴方向上的非对称性密切相关.

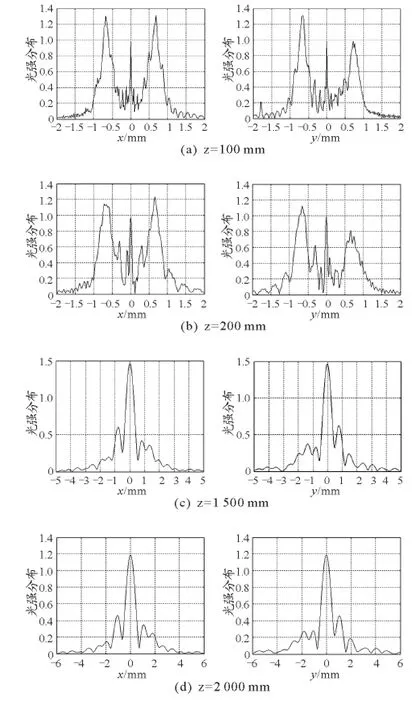
图4 平顶 －高斯光束通过R＝0.9mm的外圆与外接圆半径r＝0.8mm的三角形围成孔衍射，不同观察面上对应光强在x，y轴方向上的分布图样

4 结论

文中对平顶 －高斯光束通过圆形与三角形围成孔的衍射特性进行了研究.数值模拟结果表明衍射特性与孔径大小密切相关，通光孔径越大，菲涅耳衍射与夫琅禾费衍射转换点越远离衍射屏，即菲涅耳衍射区域越大，整体衍射光强越强，模拟结果与理论分析相符合.另一方面，夫琅禾费衍射区的观察面上只有单峰现象，传输距离越远，中心处的衍射光强越弱；菲涅耳衍射区内观察面上有多峰现象，观察屏中心的亮斑与泊松亮斑相似.再者，围成孔中三角形在x，y轴方向上的不对称性决定了菲涅耳衍射和夫琅禾费衍射图样的不对称性.

文中所用方法和所得结果可以进一步推广用于其他激光光束.通过不同形状其他衍射屏的衍射研究和计算模拟，如椭圆环孔、矩形与三角形围成孔等不规则衍射屏，具有重要的实际指导意义.上述衍射特性的研究，对于理解菲涅耳衍射和夫琅禾费衍射具有一定的参考价值.对于利用其他数值积分求解，如高斯积分、复合梯形积分、快速傅里叶变换积分，有待近一步比较、研究.

1 F.Cori.Flattened Gaussian beams.Opt.Commmun.，1994，107（5，6）：335～341

2 罗时荣，吕百达.平顶高斯光束在有光阑光学系统中的传输.中国激光，2002，29（5）：425～428

3 屈军，丁培宏，孟凯，等.平顶高斯光束及其通过圆孔光阑的衍射.应用激光，2007，27（4）：318～321

4 朱莉华，聂义友，吕百达.截断平顶高斯光束M2因子的比较研究.光子学报，2007，36（3）：536～538

5 罗时荣，吕百达.三维平顶高斯光束通过环形光阑的传输特性.激光技术，2000，24（4）：256～259

6 吕百达.激光光学（第三版）.北京：高等教育出版社，2003.10～12

7 Juguan Gu，Daomu Zhao，Zhangrong Mei，et al.Propagation characteristics of linearly polarized Bessel-Gaussian beams through an annular apertured paraxial ABCD optical.Optik，2004，115（12）：529～532

8 Juguan Gu，Daomu Zhao.Propagation characteristics of Gaussian beams through a paraxial ABCD optical system with an annular aperture.Journal of Modern Optics，2005，52（8）：1 065～1 072

9 杨平，顾菊观，张亚萍，等.厄米高斯光束通过圆孔衍射的两种计算方法比较.物理与工程，2011，21（5）：20～23

10 姚启钧.光学教程（第四版）.北京：高等教育出版社，2008.76～77