基于AMESim和LS－SVM的高压共轨系统建模与仿真＊

邓元望，元 野，周 飞，陈可亮

（湖南大学 机械与运载工程学院，湖南 长沙410082）

柴油机高压共轨喷射系统是一个复杂的、非线性的、时变的系统，其过程参数随工况不断变化，建立柴油机高压共轨系统模型是对其进行控制和优化的前提，国内外在这方面进行了大量的研究[1－2].用传统建模方法建立整个系统的数学模型时，包含的数学方程多，求解难度大，计算结果的准确度也不高[3]，因此需要进一步完善共轨系统仿真模型.

基于神经网络的非机理建模方法用于建立柴油机高压共轨系统模型，也取得了较好的结果，但该方法是基于大样本数据条件下获得的，需要大量的实验数据，同时该方法在处理随机性和时变特性方面的效果并不理想[4－5].支持向量机方法与神经网络方法都能对复杂的非线性系统进行拟合，但在针对小样本的泛化能力方面，支持向量机方法明显优于神经网络方法.目前支持向量机已广泛应用于模式识别与时间序列预测中[6]，取得了很好的效果.

本文通过对柴油机高压共轨喷射系统结构和工作过程的分析，在AMESim仿真软件中建立包括高压油泵、共轨管部件和共轨喷油器在内的共轨系统模型，研究各参数对共轨压力的影响.并用灰色关联分析数据确定出共轨模型的输入参数，再用最小二乘支持向量机（LS－SVM）对高压共轨系统进行拟合，根据仿真软件所得的样本数据训练该模型，并与BP神经网络拟合进行性能对比，验证高压共轨模型的精确性.

1 基于AMESim的高压共轨系统模型

高压共轨系统由燃油低压子系统、共轨压力控制子系统、燃油喷射控制子系统、电控发动机管理系统组成.低压油从油箱进入三柱塞高压泵产生高压油，经高压油管进入共轨管（Rail），分配到喷油器入口端，通过控制喷油器电磁阀控制喷油.当共轨压力超过一定数值时，限压阀（Flow Limiter）开启进行卸压.本文利用AMESim软件的发动机仿真平台IFP－Engine，建立了四缸直喷柴油机仿真模型.

1）将现实的物理模型加以抽象，转化为AMESim软件中的各个模块.

高压油泵（Supply pump）部分包括：凸轮模块、柱塞模块、出油阀模块、PCV模块、回油阀模块.

共轨（Rail）部分包括：共轨容积模块、共轨各部分相对位置.

喷油器（Injector）部分包括：电磁阀驱动力模块、球阀腔模块、进（回）油孔、控制腔模块、控制活塞、顶针、针阀体、喷嘴内油管、控制腔、盛油槽、压力室容积、喷油嘴、喷孔数目及直径、回位弹簧的刚度及预紧力、针阀的泄露、回油压力.

2）在AMESim中将这些子模块按共轨系统的结构连接起来，组成后的高压共轨系统模型，如图1所示.为了便于观察，图中高压油泵、调压阀、限压阀和喷油器均为封装后的超级元件.

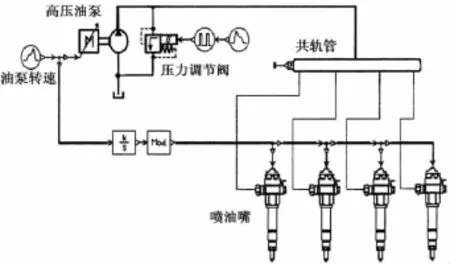
图1 高压共轨系统模型Fig.1 The model of high－pressure common rail system

在AMESim软件中建好模型后，根据高压共轨台架结构参数及其试验条件设定共轨系统模型参数，选取的共轨系统参数为压力控制阀开启角（PCV＿ON）、泵油量（Vp）、喷油器电磁阀信号（TWV）、共轨容积（Vr）和柱塞泵转速（Rp）、共轨压力（Pr），见表1.再利用软件中的批运行功能研究了不同参数下共轨管压力的建立过程，并进行模型验证.仿真与试验结果如图2所示.

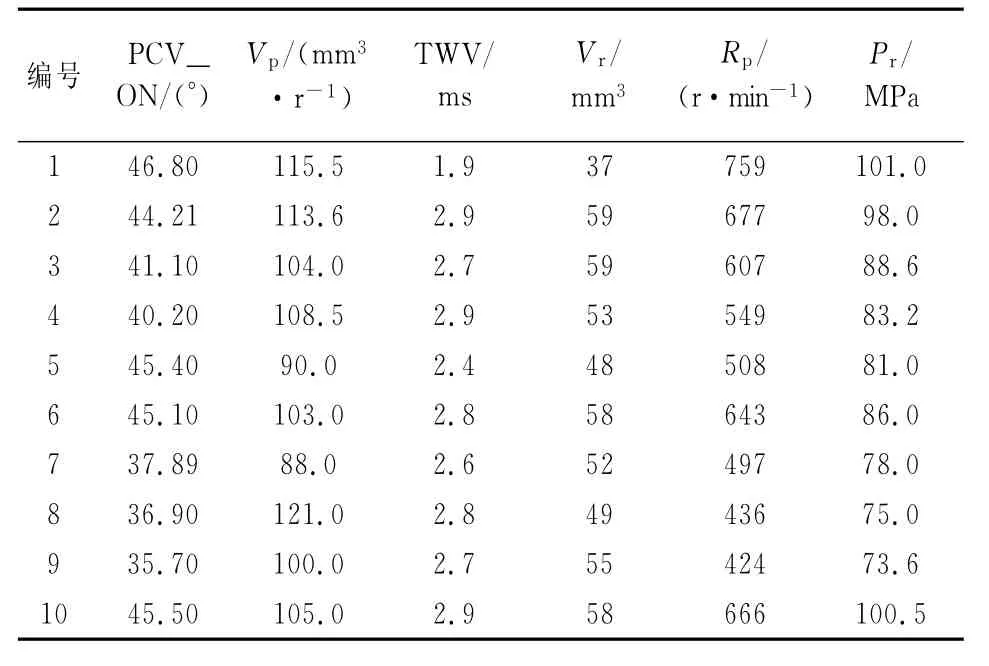
表1 轨压影响因数Tab.1 The Impact factors of rail pressure

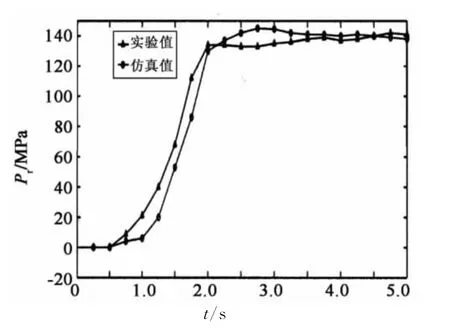
图2 压力建立过程的实验结果与仿真结果比较Fig.2 Comparison between the simulation result and the experimental result based on pressure built－up process

由图中可以看出，该仿真模型的仿真结果与试验结果具有一致的趋势，能很好地跟踪共轨压力的实际情况.建立的基于AMESim的高压共轨系统仿真模型准确，基本上可以对系统进行仿真研究.

2 基于灰色关联分析方法的模型输入参数

灰色关联分析是灰色系统理论的一个重要组成部分，它通过计算关联因素变量的数据序列和系统特征变量数据序列的灰色关联度，进行大小排序确定事物之间的关联度强弱[7－8].本文采用灰色关联分析方法计算影响共轨压力各因素的关联度大小，以此来确定共轨模型的输入参数.

2.1 确定参考数列与比较数列

为了对参评对象数据序列进行评价，首先要确定评价参考数据序列与比较数据序列.本文将共轨压力作为参考数列，记为x0（k）；把压力控制阀开启角、泵油量、共轨容积、油泵转速、喷油器电磁阀信号作为比较数列，记为xi（k）（i＝1，2，…，5；k＝1，2，…，10）.

2.2 原始数据的规范化处理

鉴于原始数据（见表1）中各计量单位各不相同，需将原始数据进行无量纲化处理，即指标区间化和归一化处理：

2.3 计算关联系数

对应于一个参考数据序列，有若干个比较数据序列，则第i个比较数据序列与参考数据序列在对应的第k个指标的相对差即为关联系数.利用式（2）计算出每个时刻点上参考数列与5个比较数列差的绝对值：

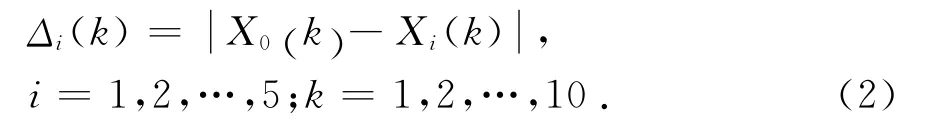
根据式（2）计算出的结果计算参考数列与各比较数列的关联系数：

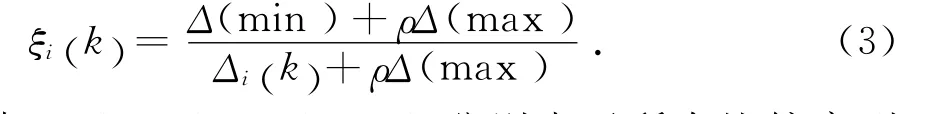
式中：Δ（min），Δ（max）分别表示所有比较序列各个时刻绝对差中的最大值与最小值；ρ为分辨系数，一般取0.5.计算结果见表2.

2.4 计算灰色关联度

关联度由关联系数的平均值求出：

由式（4）计算可得：r1＝7.298，r2＝7.133，r3＝4.988，r4＝4.943，r5＝8.437.根据结果r5＞r1＞r2＞r3＞r4可知，压力控制阀开启角、高速柱塞泵转速、油量的关联度大于共轨容积和喷油器电磁阀信号.因此选取前3个参数作为共轨压力仿真模型的输入参数.

表2 灰色关联系数Tab.2 Grey relation coefficient

3 最小二乘支持向量机及自适应权重粒子群优化方法

3.1 最小二乘支持向量机（LS－SVM）

根据支持向量机理论，对于所给的非线性样本（x1，y1），（x2，y2），…，（xk，yk）（k＝1，2，…，N）（xk为输入数据，yk为输出数据）的拟合问题可以转化为对式（5）的求解：

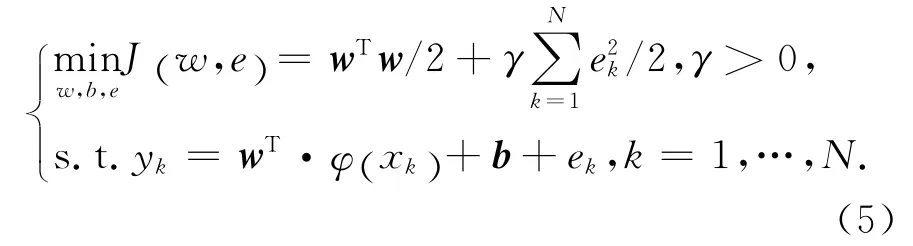
依据最小二乘理论，将式（5）转化为如下矩阵方程：

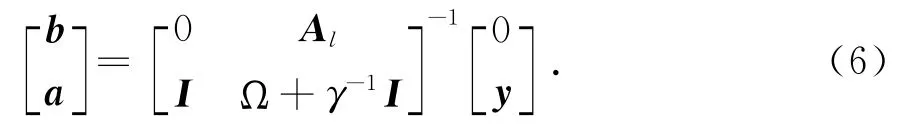
式中：y＝｛y1，y2，…，yl｝T；Al＝｛1，1，…，1｝；a＝｛a1，a2，…，al｝T；I为单位矩阵；Ω ＝φ （x）Tφ（xk）＝ K（x，xk），K（x，xk）为核函数.

本文采用高斯径向基函数（RBF）作为核函数.式（6）为一线性方程组，可用最小二乘法求解得出a，b的值，最后代入式（8）可得到在输入空间中所用的非线性分类决策函数：

将最小二乘支持向量机用于共轨压力仿真，从AMESim所得数据中随机选取100个训练样本，则式（8）中的N ＝80，输入为3维向量：｛PCV＿ON，高压油泵油量，转速｝，输出向量为共轨压力.

在LS－SVM方法中，可调正规化参数γ和核参数σ作为一个整体来使用，并且直接决定着LSSVM的训练和泛化性能.本文利用具有快速全局优化特点的改进后的自适应权重粒子群（SA－PSO）方法[9]确定γ和σ的值.

3.2 自适应权重粒子群优化算法（SA－PSO）

在粒子群算法的可调参数中，惯性权重w是最重要的参数.惯性权重w取较大值有利于提高算法的全局搜索能力，而较小的w会增强算法的局部搜索能力，根据不同的权重变化公式，可以得到不同的PSO算法[10－11].此处采用非线性的动态惯性权重系数公式[12]：

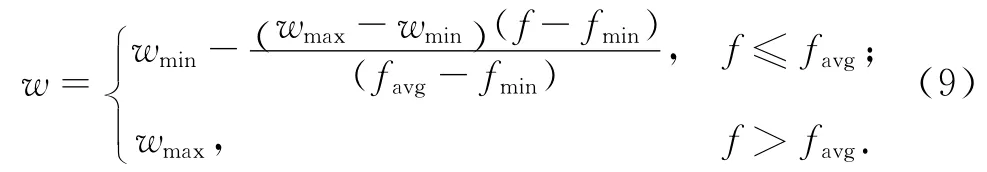
在式（9）中，惯性权重随着微粒的目标函数值f的变化而自动改变.当微粒的目标值趋于一致或者趋于局部最优时，将使w值增加；而各微粒的f值比较分散时，将使w值减小；同时f值大于平均目标值favg的微粒，其对应的w值较小，从而保护了该微粒，反之对于f值小于favg的微粒，其对应的w值较大，使得微粒向更好的搜索区域靠拢.这种自适应权重粒子算法能够平衡PSO算法的全局搜索能力和局部改良能力[12].

4 基于LS－SVM的共轨压力预测模型

4.1 SA－PSO优化LS－SVM 的关键参数

自适应权重粒子群优化算法[13]所要优化的参数为正规化参数γ和核函数参数σ.此处参数选择如下：种群数目N＝40，待优化的参数量即问题的维数D＝2，最大迭代次数M＝200，学习因子c1和c2均取2，最大惯性权重wmax＝0.9，最小惯性权重wmin＝0.6.将训练样本误差的均方差作为目标值返回.目标值表达式为：

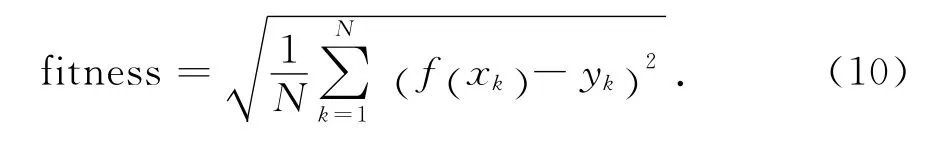
式中：f（xk），yk分别为 LS－SVM 的期望输出值与训练输出值.基于SA－PSO算法的参数寻优算法流程图如图3所示.

4.2 基于SA－PSO优化LS－SVM后的共轨压力预测

通过自适应粒子群算法优化，最后得到正规化参数γ以及核函数参数σ的最优参数组合值，分别为γ＝60，σ＝1.2.利用最小二乘支持向量机对共轨系统的共轨压力进行拟合.图3为基于LS－SVM的共轨系统模型的共轨压力预测值与实际值的比较曲线.

从图4可知，LS－SVM的预测精度较高，并且较好地跟踪了共轨压力的变化趋势.经对比预测值与实际值可知，基于最小二乘支持向量机模型的最大相对误差为7.9%，最小相对误差为1.07%，平均相对误差为3.96%.该方法表现出很好的泛化能力，测试样本的泛化均方误差仅为0.079 1.

4.3 最小二乘支持向量机模型与神经网络模型预测结果的比较

采用BP神经网络方法时，由于拟合的对象模型具有3个输入参数、1个输出参数，可根据2n＋1（n为输入层个数）求出隐含层节点数为7个，则该网络结构为3－7－1[14].隐含层函数用tansig，因为油压为正值，所以输出层函数取logsig.训练算法选用Levenberg－Marquardt法.

图3 SA－PSO参数优化流程图Fig.3 SA－PSO parameter optimization flow chart

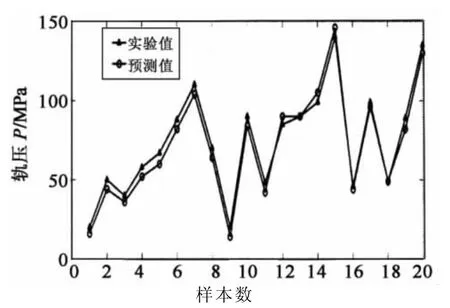
图4 共轨压力预测值与实际值的比较Fig.4 Comparison of rail pressure between the forecast and actual results

神经网络训练样本仍旧选用前文中的80个样本，选取剩下的20组数据作为检测样本，对训练好的BP神经网络模型进行检测.本文仅比较最小二乘支持向量机、BP神经网络二者预测误差，见图5.

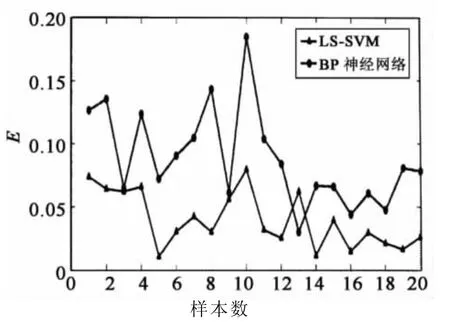
图5 LS－SVM与神经网络拟合误差比较Fig.5 Comparison of the fitting error between LS－SVM and Neural networks

由图5可见，基于BP神经网络模型的最大相对误差为18.4%，最小相对误差为3.2%，平均相对误差为9.01%；比较可知最小二乘支持向量机模型拟合误差明显小于神经网络模型.

5 结 论

本文基于AMESim建立了高压共轨系统仿真模型，对不同参数影响下的共轨系统进行仿真计算，并与试验数据进行对比，结果显示本文建立的共轨系统模型较准确.并利用灰色关联分析方法对影响共轨压力的参数进行分析评估，得出影响高压共轨轨压关联度较大的3个参数.再依据AMESim软件所得数据作为训练样本，建立了基于最小二乘支持向量机高压共轨压力预测模型，最小二乘支持向量机参数γ＝60，σ＝1.2，最后将最小二乘支持向量机模型与BP神经网络模型进行了比较，表明了最小二乘支持向量机高压共轨压力预测模型在预测高压共轨压力方面的优越性.

[1] AHLIN K.Modeling of pressure waves in the common rail diesel injection system[D].Linköping，Sweden：Linköping University，Dept of Electrical Engineering，2000.

[2] GAUTHIER C，SENAME O，DUGARD L，et al.Modeling of a diesel engine common rail injection system [C]／／Proceedings of IFAC2005.Trondheim，Norway：NTNU，2005.

[3] 颜松，魏建勤.高压共轨系统轨压模拟计算[J].液压与气动，2005（2）：3－5.YAN Song，WEI Jian－qin.Simulation of rail pressure in high pressure common rail pressure[J].Chinese Hydraulics ＆Pneumatics，2005（2）：3－5.（In Chinese）

[4] 冯宗磊，杨福源，任亮，等.发动机的组合神经网络建模[J].清华大学学报：自然科学版，2005，45（11）：1522－1525.FENG Zong－lei，YANG Fu－yuan，REN Liang，et al.Modeling of engine control systems using assembled neural networks[J].Journal of Tsinghua University：Science and Technology，2005，45（11）：1522－1525.（In Chinese）

[5] 李先成，冯静，祝柯卿，等.基于BP神经网络的GD－1高压共轨系统的建模研究[J].小型内燃机与摩托车，2008，37（1）：14－17.LI Xian－cheng，FENG Jing，ZHU Ke－qing，et al.Study on BP neural networks modeling for GD－1high pressure common rail system[J].Small Internal Combustion Engine and Motorcycle，2008，37（1）：14－17.（In Chinese）

[6] KULKARNI A，JAYARAMAN V K，KULKARNI B D.Support vector classification with parameter tuning assisted by agent－based technique[J].Engineering，2004，8（3）：311－319.

[7] 刘思峰，谢乃明.灰色系统理论及其应用[M].北京：科学出版社，2008：44－71.LIU Si－feng，XIE Nai－ming.Grey system theory and its application[M].Beijing：Science Press，2008：44－71.（In Chinese）

[8] 曲晓慧，乔新勇，陈玫，等.基于灰色关联分析的柴油机状况评估[J].兵工学报，2005，26（4）：557－559.QU Xiao－hui，QIAO Xin－yong，CHEN Mei，et al.Condition evaluation for diesel engine based on grey relation analysis[J].Acta Armamentarii，2005，26（4）：557－559.（In Chinese）

[9] NIKNAM T，FARSANI E A.A hybrid self－adaptive particle swarm optimization and modified shuffled frog leaping algorithm for distribution feeder reconfiguration[J].Engineering Applications of Artificial Intelligence，2010，23（8）：1340－1349.

[10] SUYKENS J A K，BRABANTER J D，LUKAS L，et al.Weighted least squares support vector machines：robustness and sparse approximation [J].Neurocomputing，2002，48（1／4）：85－105.

[11] KENNEDY J，EBERHART R C.Particle swarm optimization[C]／／Proceedings of IEEE International Conference on Neural Networks.New York：IEEE，1995：1942－1984.

[12] LI Xiu－fen，FU Hong－jie，ZHANG Chang－heng.A self－adaptive particle swarm optimization algorithm.[C]／／Proceedings of IEEE International Conference on Computer Science and Software Engineering.New York：IEEE，2008：186－189.

[13] 吴晓刚，王旭东，余腾伟.磁粉离合器自适应权重粒子群优化模糊控制的研究[J].汽车工程，2010，23（6）：511－513.WU Xiao－gang，WANG Xu－dong，YU Teng－wei.A research on the fuzzy control of magnetic powder clutch based on adaptive weight particle swarm optimization[J].Automotive Engineering，2010，23（6）：511－513.（In Chinese）

[14] 梁峰，冯静，肖文雍，等.BP神经网络在高压共轨式电控柴油机故障诊断中的应用[J].内燃机工程，2004，25（2）：46－49.LIANG Feng，FENG Jing，XIAO Wen－yong，et al.Application of BP nerual network to fault diagnosis of high－pressure common rail fuel system of electronic control diesel engines[J].Chinese Internal Combustion Engine Engineering，2004，25（2）：46－49.（In Chinese）