新型交错桁架结构体系的反应谱分析

苗广威，冉红东

(西安建筑科技大学，陕西西安710055)

0 引 言

交错桁架结构体系具有经济、高效的优点，是一种符合我国建筑结构发展方向的新型结构形式[1]。常用于交错桁架结构体系的桁架形式有混合式和空腹式。已有研究表明[2-5]，混合式桁架能够提供较大的侧向刚度，提高结构体系的承载能力，有利于建筑空间的灵活布置，但是混合式结构体系的延性性能差，结构体系在水平荷载作用下的破坏呈脆性的特征，不宜用于高烈度地区。

偏心支撑钢结构是近年来提出的新型结构形式，由于其固有的优良抗震性能，偏心支撑主要应用于8度及其以上抗震设防的高层钢结构房屋[6]。

为了结合上述二者各自的优点，本文将偏心支撑的结构形式用于混合式交错桁架结构体系，形成一种新型交错桁架结构体系。通过耗能段吸收和耗散地震能量，从而在很大程度上提高混合式交错桁架结构体系的抗震能力。

1 确定设计反应谱曲线

我国抗震设计用的加速度反应谱称为地震影响系数曲线。《建筑抗震设计规范》(GB50011-2010)[7]5.1.4中指出建筑结构的地震影响系数应根据烈度、场地类别、设计地震分组和结构自振周期以及阻尼比确定。水平地震影响系数最大值按照文献[7]中表3-2采用。特征周期应根据场地类别和设计地震分组按文献[7]中表3-3采用。《建筑抗震设计规范》8.2.2中规定多遇地震下的计算:高度不大于50 m时，可取0.04；高度大于50 m时且小于200 m时，可取0.03；高度不小于200 m时，宜取0.02。

综上所述，得到的数值如下:水平地震影响系数最大值为0.16；场地特征周期为0.35；阻尼比为0.03。

2 算例设计

采用的算例总高度55 m，共18层，首层层高4 m，其他层高3 m，建筑主体长24 m，宽17.6 m，交错桁架结构平面图和立面图如图1所示，桁架中杆件尺寸如图2所示(图中标注单位为mm)。研究表明[8-9]，每层腹杆塑性铰的发展顺序是从中间向两边，说明中间腹杆承受的轴力较大，因此将耗能段设置在桁架的空腹节间两侧，如图2所示。桁架腹杆与弦杆铰接；弦杆与弦杆刚接；柱与弦杆铰接；柱与基础较接。楼板厚度为120 mm，混凝土强度等级为C30。主体结构选用Q345B钢材。恒载标准值3.0 kN/m2，活载标准值 2.0 kN/m2，基本风压 0.35 kN/m2，雪载标准值0.25 kN/m2，地面粗糙度为B类。结构抗震设防烈度为8度，设计地震加速度为0.2 g，场地类别为Ⅱ类，设计地震分组为第一组。

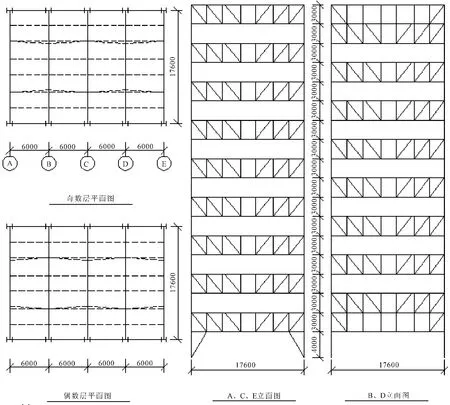
图1 交错桁架结构平面图和立面图

为了考察新型交错桁架结构体系的抗震性能及对耗能段位置的探讨，本文选取4个算例(如表1所示)，对其进行弹性反应谱分析。

截面类型Ⅰ中杆件截面尺寸由ETABS软件根据美国规范AISC-LRFD99进行设计，根据ETABS自动选择截面功能选出各杆件的截面尺寸(表2)；截面类型Ⅱ中杆件截面尺寸是在截面类型Ⅰ的基础上运用《高层民用建筑钢结构技术规范》[10]中式6.5.2～6.5.9对腹杆进行加强，加强后截面尺寸见表2。

3 结果及分析

3.1 层间位移和层间位移角对比

《建筑抗震设计规范》[7]5.5.1中规定的多高层钢结构的弹性层间位移角限值为1/250。

图2 耗能段的位置设置

表1 算例对比表

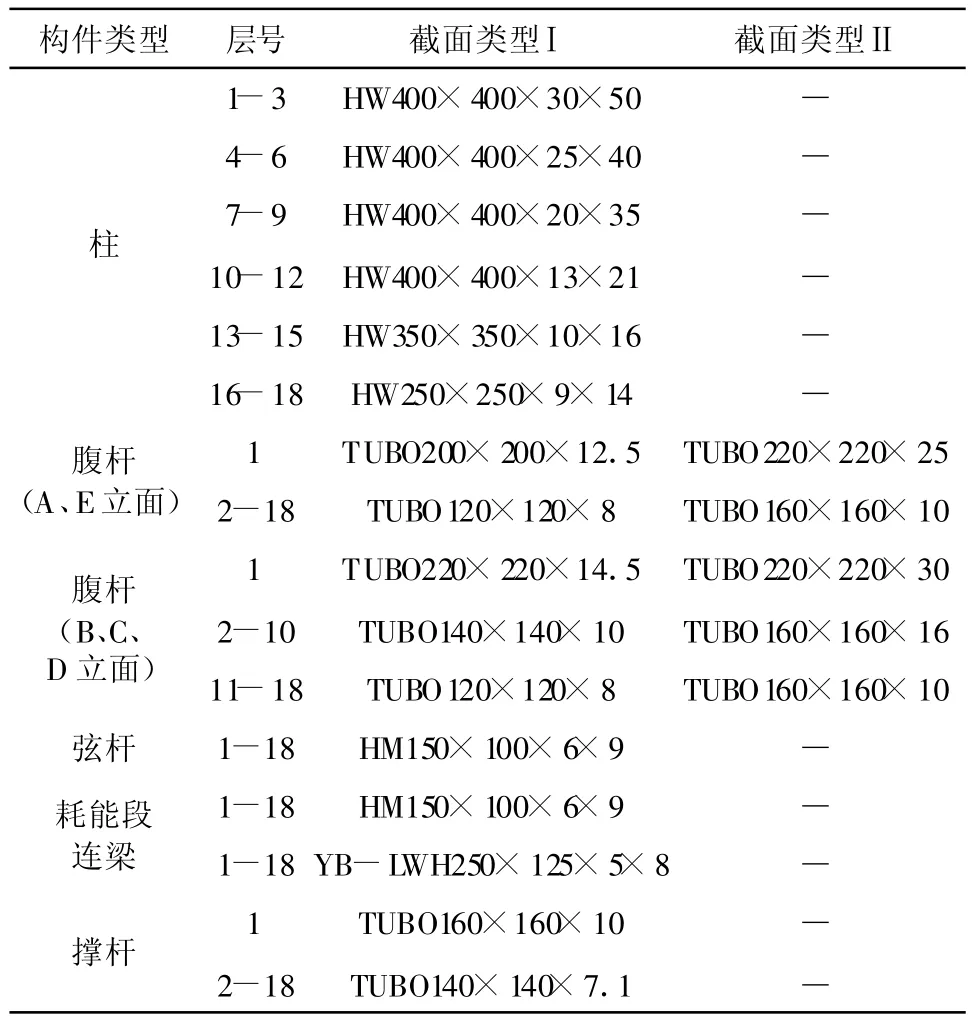
表2 各杆件截面尺寸对比表 单位:mm

图3分别绘出了相应的水平位移和层间位移角包络图。比较各层水平位移图和层间位移角包络图可得:(1)在弹性反应谱分析时，算例2的水平层间位移比算例1稍大。经过层间位移角包络图对比可得，算例2六层以下的层间位移角比算例1大，而七层以上的层间位移角基本一致。说明在弹性反应谱的作用下，由于耗能段的存在，交错桁架结构底部六层的层间位移增大，使结构相对变柔。(2)算例3的层间位移和层间位移角比算例1和算例2均大很多，甚至比算例4都要大。这说明耗能段设置在桁架下弦时，结构的层间位移明显加大，结构的刚度比未经加强的普通混合式交错桁架结构(算例4)还要小。分析原因为，空腹节间内没有斜腹杆，依靠弦杆传递侧向荷载，因此空腹节间是较薄弱部位，如图4所示，耗能段设置在桁架下弦时，在弹性反应谱作用下，耗能段的变形与空腹节间弦杆的变形相一致，这样相当于增加了空腹节间的节间长度，相关研究[8]表明，加大空腹节间的节间长度使结构柔性增加。(3)算例1的水平层间位移和层间位移角比算例4大很多，说明适当加强腹杆截面可以加强普通混合式交错桁架结构的抗侧刚度。(4)各算例层间位移角均在限值以下，满足规范要求；(5)层间位移角包络图出现折线形状，经分析，主要与模型有关，因为本文所选取的模型中相同的立面有立面A、C、E和立面B、D，即在相邻的两层中，桁架主要承担抗侧力的斜腹杆的数量之比为3∶2，这就意味着抗侧刚度之比为3∶2。经计算，相邻两层的层间位移比均在1.4～2.0之间，基本满足3∶2的关系。

3.2 内力对比

表3给出了算例2和算例3在最不利荷载组合(COMB38)作用下，2层耗能段的内力。由表3可以得出以下结论:(1)剪力值V最大值，两算例基本一致；(2)杆端轴力P和杆端弯矩M最大值，算例3比算例2大很多。

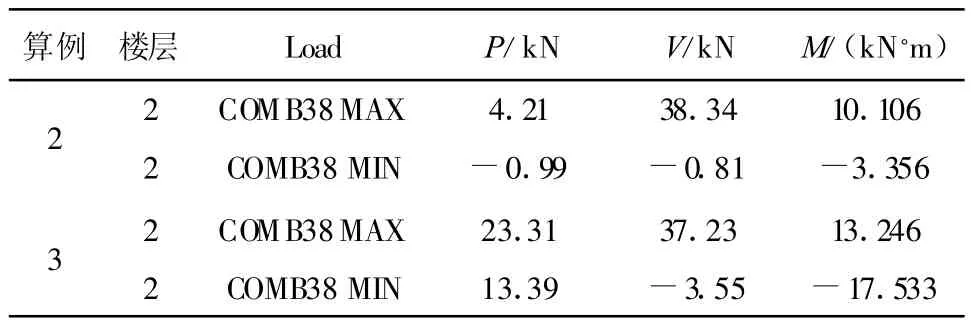
表3 不同算例耗能段内力表

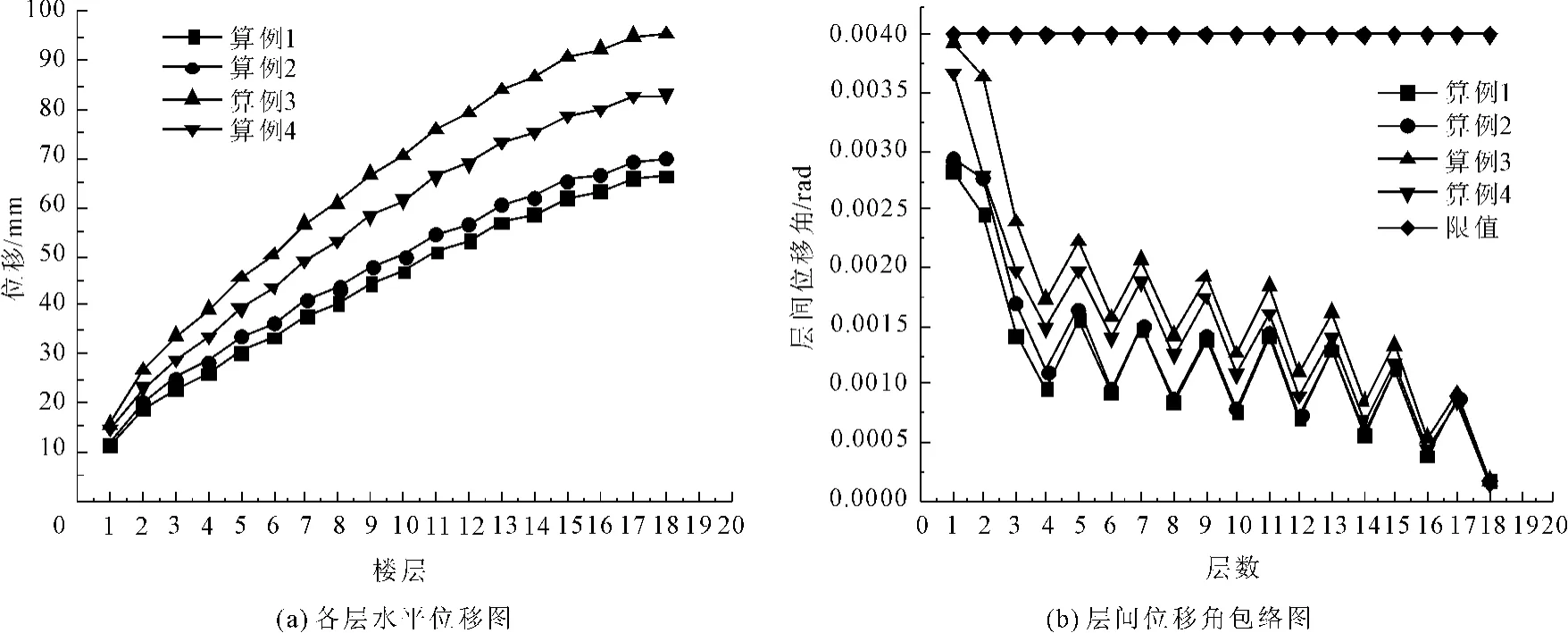
图3 反应谱分析下的各层水平位移和层间位移角包络图

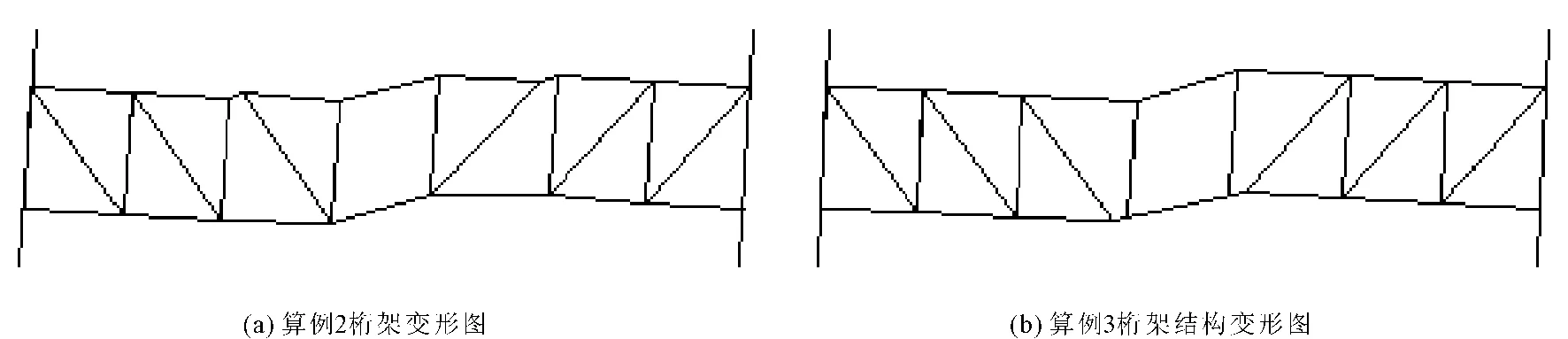
图4 不同算例的桁架变形图

表4给出了算例2、算例3和算例4在最不利荷载组合(COMB38)作用下，中间C立面1层和2层空腹节间腹杆的内力值。由表4可以得出以下结论:(1)三个算例空腹节间的上下弦杆所受轴力相差较小；(2)对比上弦杆件的剪力 V和弯矩M，算例2比算例4大，增加幅度为20%左右，算例3比算例4大，增加幅度为50%左右；(3)对比下弦杆的剪力 V和弯矩M，算例2比算例4稍大小，算例3比算例4小很多。分析以上结论可得，对比普通混合式交错桁架结构(此处指算例4)，耗能段设置在桁架上弦时，空腹节间弦杆的受力相差不大；耗能段设置在桁架下弦时，空腹节间上弦杆所受剪力V和弯矩M较大，比耗能段设置在桁架上弦更容易达到塑性，而下弦杆所受剪力和弯矩很小，即此时下弦杆的受力以轴力为主，剪力由竖腹杆传递到桁架上弦，这也解释了图4(b)中耗能段与空腹节间弦杆变形相一致的现象。

3.3 振型周期对比

规范规定，结构平面布置应减少扭转的影响；B级高度高层建筑，结构扭转为主的第一自振周期与平动为主的第一自振周期之比不应大于0.85[10]。

表5给出了不同算例第一、二、三振型的自振周期。

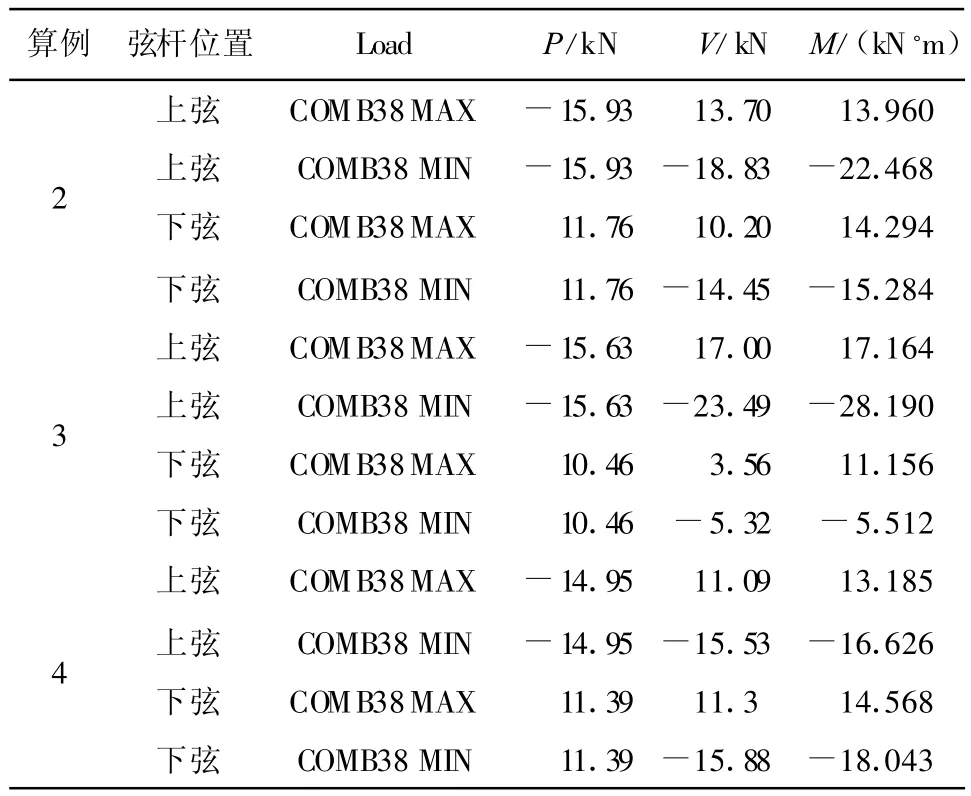
表4 不同算例空腹节间弦杆内力表

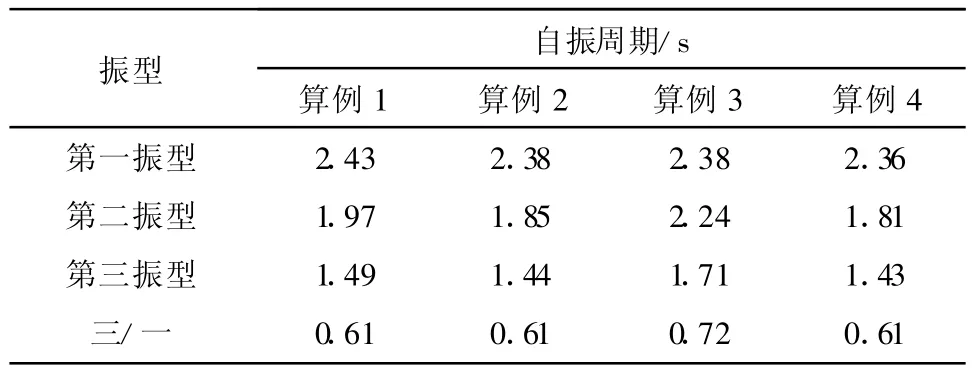
表5 不同算例的周期对比表

表5显示四个算例的第一振型均为沿着纵向的平动，第二振型均为沿着横向的平动，第三振型均为扭转。由算例1和算例4对比可得，对于普通混合式交错桁架来说，适当加强普通混合式交错桁架结构的腹杆，主要振型所对应的周期基本不变。由算例2、3、4对比得，耗能段设置在桁架下弦时，新型交错桁架接结构扭转的影响有所增加。

4 结 论

本文通过ETABS软件弹性时程分析对新型交错桁架结构体系的抗震性能进行了研究，并对耗能段的位置进行了探讨。得到结论如下:

(1)虽然耗能段设置桁架上弦和下弦都能使新型交错桁架结构比普通交错桁架变柔，抗震性能增强，并且两新型结构中的相同楼层耗能段所受剪力大小基本一致，但是耗能段设置在下弦时，耗能段的变形相当于增加了空腹节间的长度，结构的层间位移增加很多，并且空腹节间上弦杆受力较大，较容易屈曲，整体结构的扭转影响较大。因此建议将耗能段设置在桁架上弦。

(2)耗能段设置在桁架上弦时，新型交错桁架结构底部六层的水平层间位移比普通交错桁架结构大，使结构相对变柔。

[1]周绪红，莫 涛，蔡益燕，等.新型交错桁架结构体系的应用[J].钢结构，2000，15(2):16-19.

[2]Cohen M P.Design solution utilizing the staggered-steel truss system[J].Engineering Journal AISC，1986，23(3):97-106.

[3]刘红梁，刘志雄，陆钦年.交错桁架体系结构性能分析[J].哈尔滨工业大学学报，2004，36(9):1173-1176.

[4]莫 涛，周绪红，刘永健，等.交错桁架结构体系的受力性能分析[J].建筑结构学报，2000，21(6):49-54.

[5]冉红东.钢交错桁架结构体系在循环荷载作用下的破坏机理和抗震设计对策[D].西安建筑科技大学，2008:197-199.

[6]顾 强.钢结构滞回性能及抗震设计[M].北京:中国建筑工业出版社，2009:389-340.

[7]中华人民共和国住房和城乡建设部.GB50011-2010.建筑抗震设计规范[S].北京:中国建筑工业出版社，2010:32-33.

[8]周秀月.钢结构交错桁架结构体系的合理结构布置探讨与Push-over分析[D].西安:西安建筑科技大学，2005.

[9]苑 辉.钢结构设计[M].北京:中国计划出版社，2006:422-426.

[10]中国建筑研究院.JGJ99-98.高层民用建筑钢结构技术规程[S].北京:中国建筑工业出版社，1998:42-45.