相同半径的反向复曲线的应用

王保良

(黑龙江大学，哈尔滨 150080)

复曲线，目前知道的有:同向复曲线、反向复曲线和相同半径的同向复曲线。其实还有相同半径的反向复曲线，本文就此介绍该曲线的应用。

我们通常在公路各个交点分别做成单独的圆曲线，但当相邻两个交点相距较近时，采用复曲线，因为这样做，可使曲线半径得到相应的增大，有利于行车。

1 同向复曲线简介

同向复曲线见图1，其中A、B、C、D为交点(转折点)，用JD表示，α右1、α右2为向右拐弯交角。施测时，先选定公切点Q2，再量出切线长 T1、T2，及测出 α右1、α右2。根据这些已知条件，先计算出R1、R2，再进行相关的计算和测量。

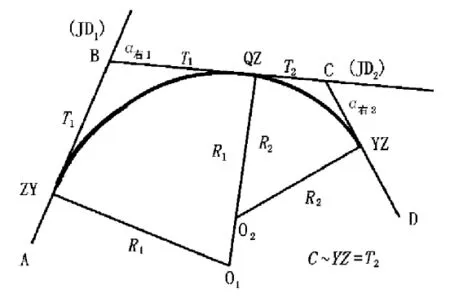
图1 同向复曲线

2 反向复曲线简介

反向复曲线见图2，同样A、B、C、D为交点，只是交角一个是右拐α右1，一个是左拐α左2。该曲线测算过程和上述基本相同，只不过第二个曲线在相反方向而已。

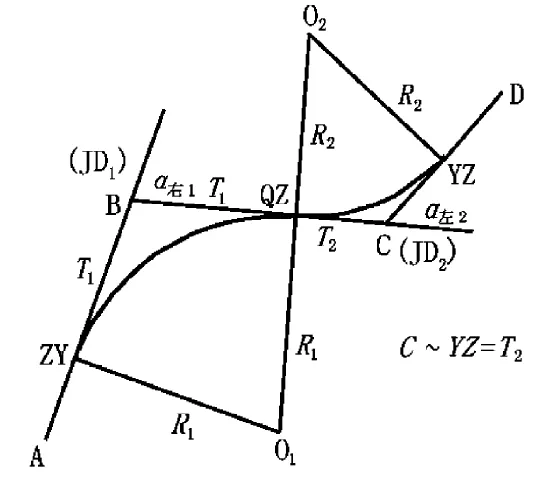
图2 反向复曲线

3 相同半径的同向复曲线

公路线路如图3中ABCD，现分别延长AB和DC相交于P点，得△BPC，而∠BPC为该三角形的内角，∠ABC及∠BCD为其外角;根据几何上定义，这三个角的分角线相交于一点O(O称旁心)，因该点到△BPC的三个边等远，以R表示，现以O为圆心，R为半径作圆，相切于AB于ZY点(曲起点)、BC于QZ点(公切点)、CD于YZ点(曲终点)，图3相同半径的同向复曲线见图3。

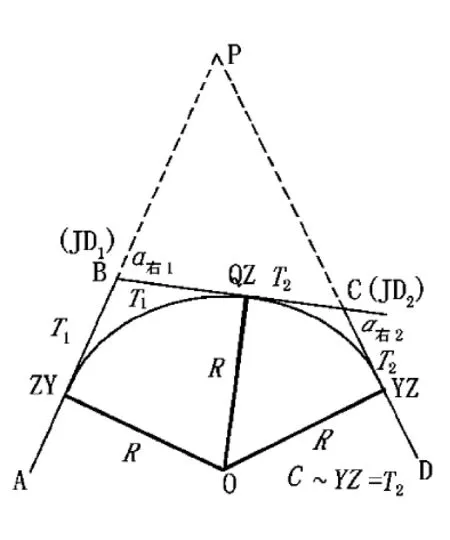
图3 相同半径的同向复曲线

现将 α右1、α右2分别测出，并丈量公切线 DBC的长度，即可推导出相同半径的同向复曲线半径R的计算公式为:

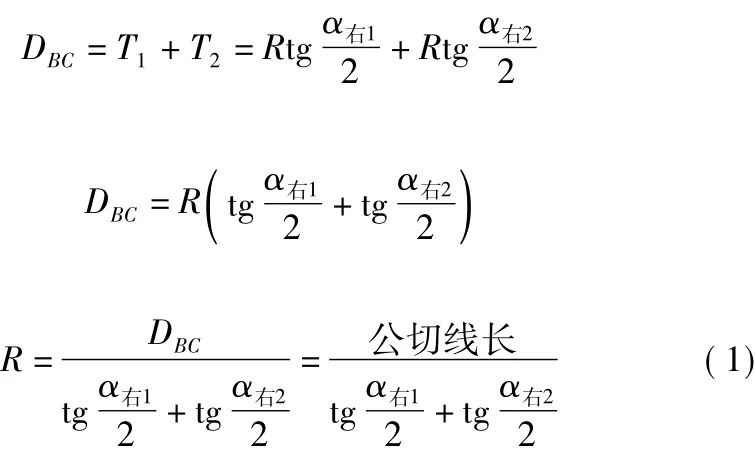
根据公式(1)，先丈量出公切线长DBC和测出α右1、α右2，就可根据公式(1)计算半径R及其相关计算和测量。

(1)式反映的是相同半径的同向复曲线半径R的计算公式。

4 相同半径反向复曲线的应用

4.1 相同半径的反向复曲线半径R计算公式的证明

首先将图3的左侧一模一样的画好，后将右侧图形以公切线BC为轴旋转180°画成相同半径的反向复曲线见图4。

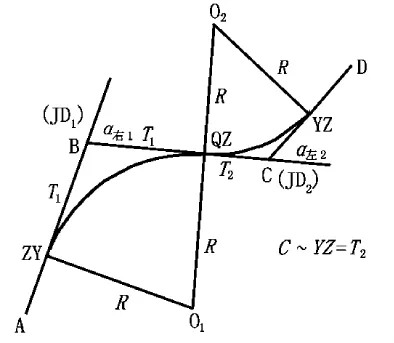
图4 相同半径的反向复曲线

从图4可以看出，公切点、公切线未变，在相反方向的扇形图大小未变，α右2成为α左后也未变。现从公式(1)中3个要素来说明:

图4中和图3中的公切线BC相同(BC=BC)

图4中和图3中的 α右1相同(α右1=α右1)

图4中的 α左2和图3中 α右2相等(α左2=α右2)

图4中和图3中R相同(R=R)

现将角名不相同但相等的α左2取代(A)式中的α右2，则得相同半径的反向复曲线半径R的计算公式为:

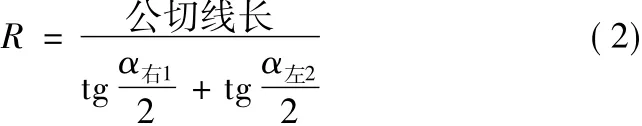
(2)式反应的是相同半径的反向复曲线半径R的计算公式。

由于(1)式和(2)式，实质相等，应设法统一。特别是同向还是反向，很好认定，公式中可不反应;现在将相邻两个交角，用 α1、α2表示，则得(1)和(2)式的统一(3)式为:

(3)式适用于图3、图4两种图形。

4.2 相同半径的反向复曲线的应用举例

例1，已知数据如图5，试计算相同半径同向复曲线的半径R。

公切线BC=1 026.32 m

解:由公式(3)得:

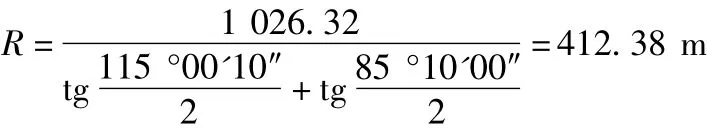
即图5中，R=412.38 m

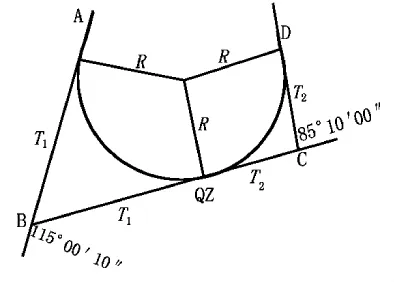
图5 相同半径的同向复曲线

例2，已知数据如图6，试计算相同半径的反向复曲线的半径R。

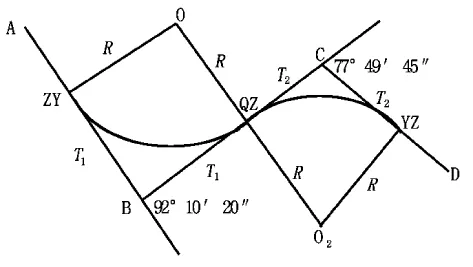
图6 相同半径的反向复曲线

公切线BC=996.64 m

解:由公式(3)得

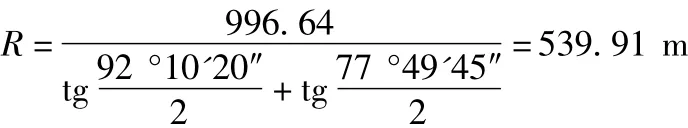
说明一点:图2、图4统称为反向曲线。反向曲线因曲线的外侧超高不好解决，因而行车要减速行走。反向曲线还不能不用，这是地形、地物的多变造成的。反向曲线多用于低等级道路，但高等级道路也是回避不了的，不过其曲线半径要大于或等于不考虑超高的情况下才行。