改进小波在调制模式识别中的应用
2012-08-10秦立龙王振宇闫朋展
秦立龙,王振宇,闫朋展
(解放军电子工程学院信息系,安徽 合肥 230037)
0 引言
在调制模式自动识别的框架内,调制模式自动调制识别一般使用统计模式识别[1]。基于统计模式识别的方法可以分成两个部分:特征提取和分类器设计。特征提取负责对接收到的信号提取出最能表现其调制特征的参数。分类器则根据已提取出的特征把信号划分到相应的类别。现有的数字调制模式识别特征提取算法主要归纳为以下几种:基于瞬时信息的特征提取、基于时频分析的特征提取、基于累积量的特征提取、基于谱相关法的特征提取等。
针对通信信号调制模式的特点,提出了一种新的特征提取方法,将最优插值估计算法用于预测器的设计。经过仿真证明,这种基于最优插值估计的提升小波效果优秀,符合工程需要。
1 小波变换简述
第2代小波变换[2]是Swelden提出的一种不依赖于傅里叶变换的小波构造方法,小波基构造方法灵活,算法简单,执行效率高。第2代小波变换将传统小波变换过程分为分裂、预测和更新3个阶段。
(1)分裂

(2)预测
对于一个局部相关性较强的信号,它的偶子集和奇子集是高度相关的,因此,知道其中任何一个,就有可能在它合理的精度范围内预测另一个。记预测算子为P,预测误差 dj-1即为:

(3)更新

2 小波变换的改进
为了有效地提取分析信号的特征,使P的选择能够反映信号的结构,将最优估计方法[3]引入 P的设计,以期获得一组最优的预测系数,即寻找一组P使目标函数J=dTd最小。使用相邻的2D (D为正整数)个偶样本来进行估计,设:

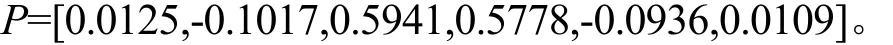
3 特征的提取
首先利用MATLAB产生了高斯白噪声信道下7种待识别数字信号的仿真数据,这7种常用数字调制信号为:2ASK、4ASK、2FSK、8FSK、MSK、4PSK、8PSK、16QAM信号,主要调制参数为:载频fc=10 kHz,采样频率fs=200 kHz,MSK码元速率fb=4×fc/5,其他信号码元速率为fb=2 000 B,频率偏移量Δf =2 000 Hz。提取的特征参数定义如下:
三要大力培育农民用水户协会等群管组织,建立完善村级水管员制度,使每一项农水工程都落实好管理主体。要建立和完善收费补偿机制,实行政府补贴,通过业主招标、承包租赁等方式,保障投入农田水利设施资金的合理效益。

std(·)表示标准差算法,di为第 i层分解的细节系数。通常均值差别越大,类间分离越好;方差越小,类内聚集越好。对7种调制信号以间隔1 dB变化加入信噪比为0~20 dB的噪声,每种特征参数各取150个特征样本,计算特征参数的均值。以第三层特征分解为例,仿真结果如图1所示。
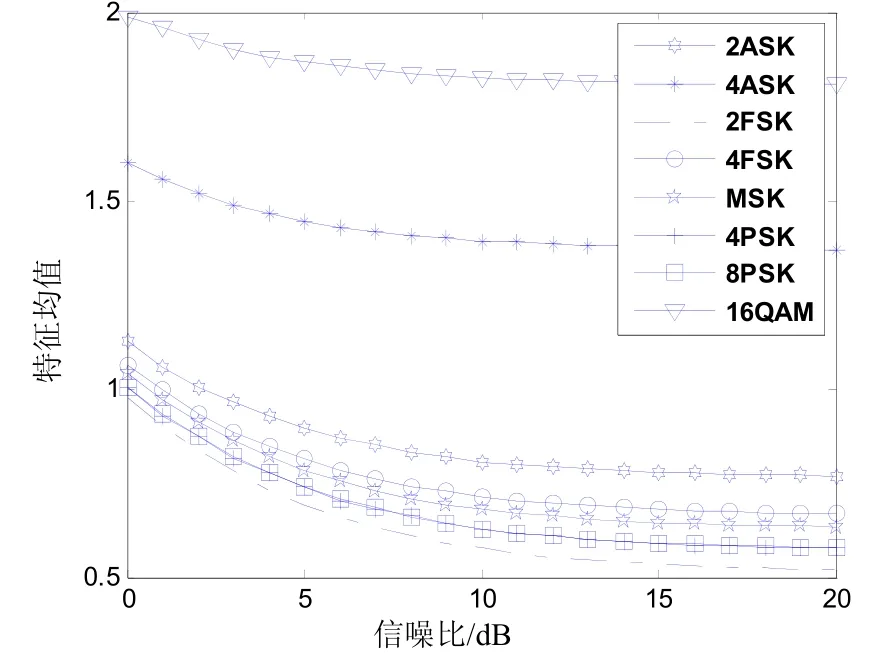
图1 第三层分解数据的标准差随信噪比变化曲线
由图可得,不同调制方式的信号特征差别较大,所以提取的分类特征能实现其类间、类内识别。

表1 信噪比为5 dB时归一化特征参数均值的方差
通过表1可以看出,改进的第二代小波方差较小,表明算法得到的数据类内聚集较好。在此基础上,可以进一步进行调制模式识别。
4 特征识别性能分析
4.1 分类器的设计
支持向量机(SVM,Support Vector Machine)是依据统计学习理论提出的一种机器学习方法[5]。它是以结构风险最小化准则来实现的,其鲁棒性强,结构简单、推广性好,弥补了神经网络分类器存在的固有问题,具有很大的优越性。分类器使用径向基核函数[6],其表达式为:

分类器的结构采用二叉树支持向量机。由于类距离算法在分类问题中性能优良,并且推广性能好,所以依据该算法生成二叉树结构。经计算机仿真确定的二叉树分类向量机结构为:16QAM、4ASK、2ASK、2FSK、MSK、4FSK、4PSK、8PSK。
4.2 最优参数值的确立
在实际应用中,需要事先确立向量机中两个参数(惩罚因子c和核参数σ),不同的参数值,向量机的分类性能也不尽相同。利用粒子群算法[7]来寻找最优的参数值,参数σ、c的搜索空间均设为0~1000,以分类正确率作为粒子群算法的适应度值。流程如下:
1)初始化种群中粒子的位置(σ、c)和速度。
2)根据不同的核参数σ、c,计算各粒子的适应度值(分类准确率),并得到各粒子迄今为止最优位置和群体迄今为止最优粒子位置。
3)根据式(7)计算自适应惯性权重:
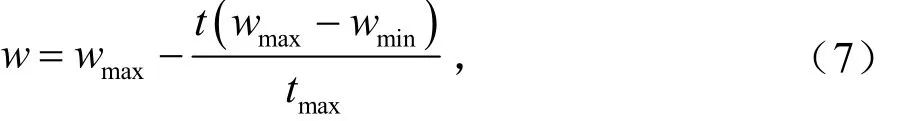
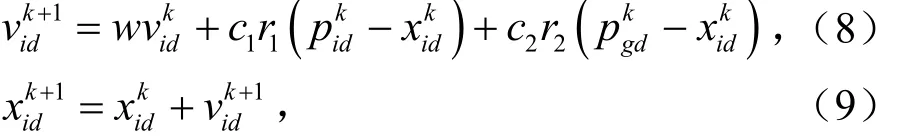
更新粒子速度和位置。
4)判断是否满足最大迭代次数。若满足,算法结束并输出最优参数值和正确率,否则,迭代次数加1,转向步骤2。
4.3 性能仿真与分析
每种信号提取样本数为150 个,其中50 个样本用于向量机的训练,100个样本用于正确率的测试,得到分类正确率曲线如表2所示。
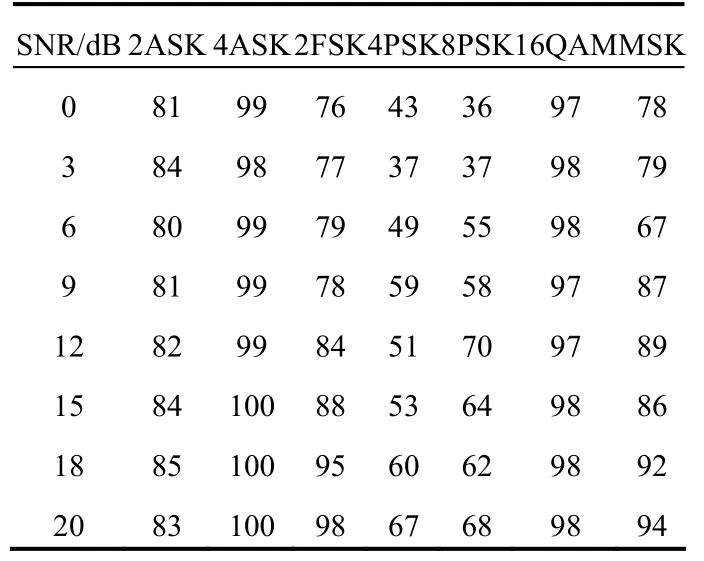
表2 不同调制方式分类正确率(单位∶%)
计算机仿真结果表明:在信噪比为0~20 dB的情况下,基于改进第二代小波的特征识别方法能够得到较高的调制模式正确识别率,说明新算法能够很好的分析信号,证明其具有良好的有效性。
文献[8]中利用 sym4基小波分解细节系数,然后计算标准差作为特征参数。sym4小波具有很多的优良特性,因此选用此小波函数进行对比很有意义。仿真得到两种小波分类正确率曲线如图2所示。
仿真结果表明:改进的提升小波与sym4小波相比,能够得到更高的调制模式识别正确率,说明新算法能够更好的分析信号,具有更好的有效性。
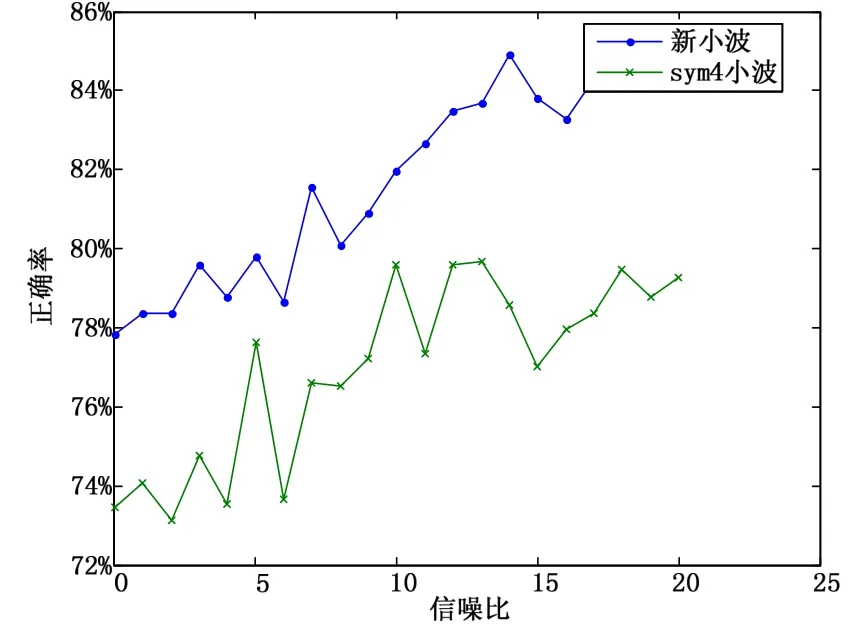
图2 分类正确率随信噪比变化示意
5 结语
针对 7种常用数字调制信号进行了计算机仿真,仿真结果表明:改进的提升小波在使特征值具有更好的特征均值和方差的同时,降低了算法的复杂度,提高了识别的正确率,充分说明新算法具有更好的有效性和工程应用性,但是在识别PSK信号时效果欠佳。如何改进PSK信号的识别正确率,是接下来需要研究的方向之一。
[1] 唐峰,蒋兴浩,孙锬锋,等.基于多特征融合的运动对象识别算法[J].信息安全与通信保密,2012(03):57-58.
[2] 杨扬,邓家先,吴昊.提升小波高速分解的系统设计与实现[J].通信技术,2011,44(04):16-18.
[3] 段晨东,姜洪开,何正嘉.一种改进的第 2代小波变换算法及应用[J].西安交通大学学报, 2004,38(01):47-50.
[4] FERNANDEZ G, PERIASWAMY S, SWELDENS W. Liftpack:a Software Package for Wavelet Transforms Using Lifting[J]. Proc of SPIE on Wavelet Applications in Signal and Image Processing. 1996,2825(04):396-408.
[5] 张学工.关于统计学习理论与支持向量机[J].自动化学报, 2000, 26(01):32-42.
[6] 王玲霞,袁佳,张效义.基于小波包变换的辐射源信号特征提取和识别[J].通信技术,2009,42(03): 215-217.
[7] KENNEDY J, EBERHART R C. Particle Swarm Optimization[C].USA:IEEE, 1995:1942-1948.
[8] 闫朋展.基于特征选择和BT-SVM的数字调制模式识别研究[D].安徽:解放军电子工程学院,2011.
