一种基于自相关函数的载波频偏估计方法

龚岳洲，周新力，王文琰，鞠振飞

（①海军航空工程学院，山东 烟台 264001；②海军装备部驻上海地区军事代表局，上海 200000）

0 引言

载波同步的是数字通信系统必须解决的问题，消除发送端和接收端载波频率的偏移是载波同步的关键技术。由于突发通信具有短时性、隐蔽性和不易截获的特点，被广泛应用于军事通信，必须实现快速的载波同步[1]。

文献[2]给出了在高斯白噪声中对正弦波信号频率进行最大似然估计(MLE，Maximum Likelihood Estimation)算法，估计误差的方差达到了克拉美罗限，因此是最优估计.由于 MLE算法计算量大，难以实时进行处理。于是提出了很多基于最大似然估计的简化算法，Kay在1989年提出了经典的Kay算法[3]，Kay算法相对于最大似然估计(MLE)算法在计算复杂度有了很大简化，但是存在较高的信噪比门限（6 dB），当接收端信噪比小于该门限时，性能急剧恶化，没有达到工程应用的要求。而针对Kay算法高信噪比门限的缺点，文献[4]提出了L&R算法，L&R算法也是基于最大似然算法的简化算法，具有很低信噪比门限（-10 dB），完全能满足工程应用要求，但频偏估计范围过窄，也不适合运用于工程上。文献[5]根据最大似然方程的另一种近似解，提出了Fitz算法,在频差较小时均能取得较高的估计精度。但是，t同样存在估计范围小的缺点，且计算复杂度较高的缺点。文献[6]提出了M&M算法，M&M算法既具有低的低信噪比门限，又能估计很大的频偏，但是复杂度太高，同步过慢，不利于实时处理。

本文利用相位折叠现象使得自相关函数的频偏具有周期化规律，基于这一思想，本文提出一种利用最大似然估计中的自相关函数进行频偏估计的算法，该算法估计范围广，精度高且复杂度低，适于突发通信。

1 信号模型

本算法采用MPSK调制方式，在高斯白噪声信道下进行传输，高斯白噪声的双边谱密度为 N0/2，采样时满足Nyquist准则，已经完成信道均衡，消除了码间干扰。并假定接受端进行载波同步之前已经进行精确的定时同步，不存在定时偏差。假设接受端的载波频率相对于发送端的载波频率有efHz的频率偏差，则接收端基带信号表达式如下：

其中，na是所要接受的信号，对于MPSK信号，可以表示为[3]：

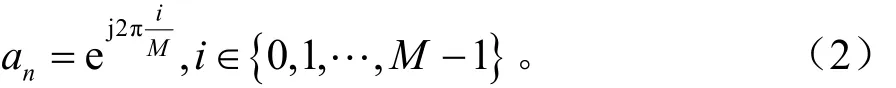
Ts是符号周期，是载波相位，θ0在观测数据长度N内，是确定的未知量，fe是需要估计的载波频偏，Nn是加性高斯白噪声，其均值为零且方差为σ2[7]。实际上由于表示 an的复数共轭），于是可以定义，即得到：在统计上是与 N 等价的，A是幅度n噪声，nθ是相位噪声，因此nb可以看成高斯白噪声下的单音正弦信号[8]。文献[3-10]提出了很多经典的方法，下面介绍一种新的频偏估计方法。

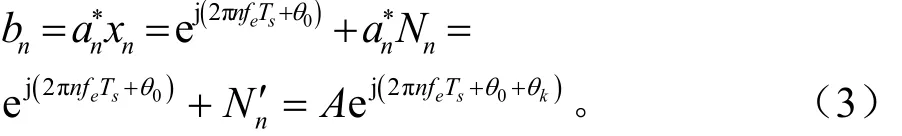
2 算法分析

由经典的最大似然估计[9]得到：

可以等效为：

令：

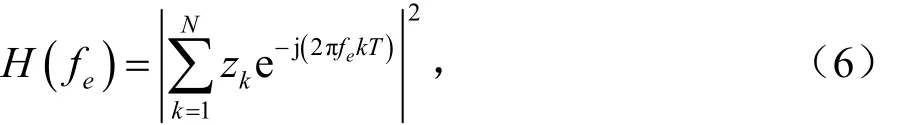
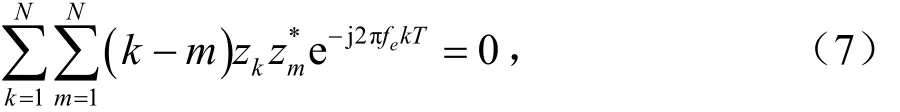
于是得到最大似然的估计方程：

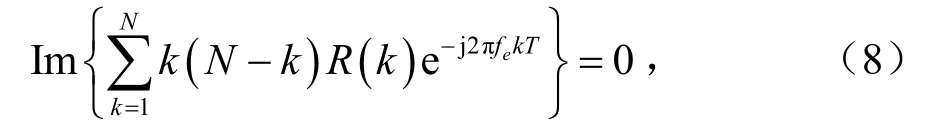
由于最大似然估计是非线性最优估计，复杂度太高，所以所以并不适用于工程实际。本文也是基于 R （k）得到的一种频偏估计方法。

实际上R(k)可以写成[10]:

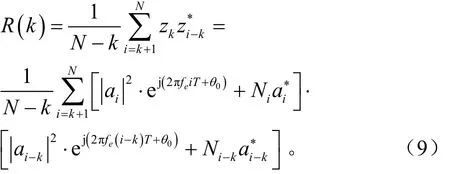
可得简化的公式：

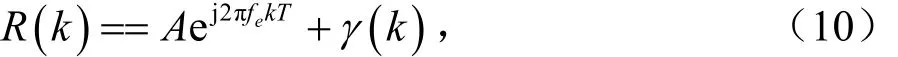
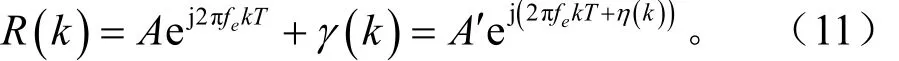
η（ k ） 表示复噪声 γ （ k ） 在相位上的噪声。定义arg（R（ k ） ） 为 R （k） 的相位，则：

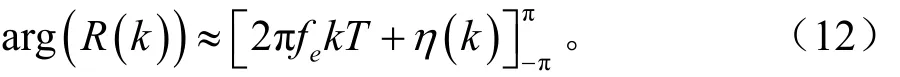
于是可得：

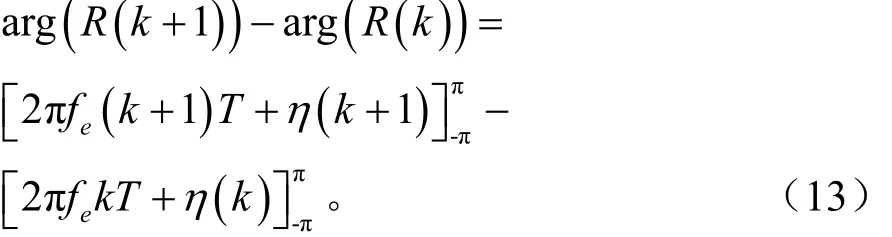
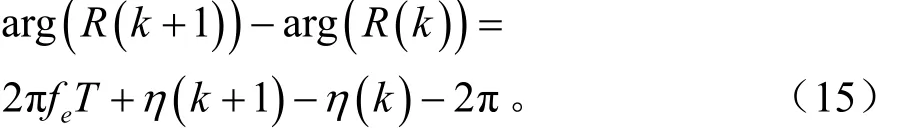
为直观的分析算法原理，先用matlab进行蒙托卡罗仿真，仿真条件：数据长度N=50，归一化频偏信噪比

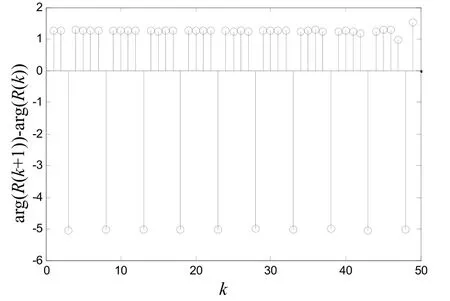
图1 arg(R(k+1))-arg(R(k))的周期变化规律

从上面的分析可以将频偏的估计转化为对M的估计。新算法可以描述为：

1）计算自相关函数R(k)。

3）当频偏大于零时，设定闸值 H，得到 X+1个 k 满足

5）当频偏小于零时，设定闸值 H，得到 X+1个 k 满足 temp

7）求得归一化频偏feT=G/M。

接下来将从估计范围，算法复杂度三个方面来分析本算法的性能。在此之前先介绍三种基于 R(k)的经典算法。

L&R算法[4]，其表达式为：

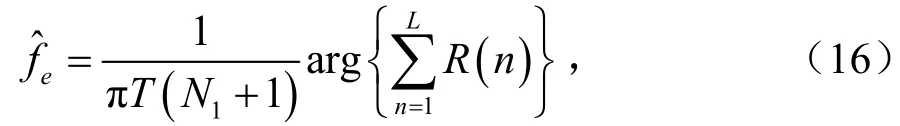
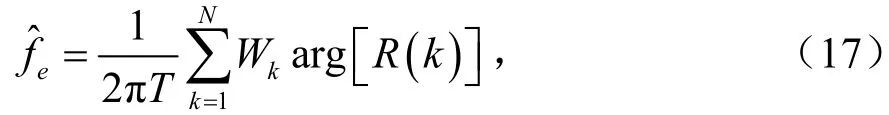
M&M算法[6], 其表达式为：

本算法的计算复杂度由于只需要计算自相关函数，相对于M&M算法有很明显的改善，对于突发通信来说本算法具有突出的优势。下表是L&R算法，kitz算法，M&M算法与本文算法在复杂度上的比较。

表1 复杂度比较

当数据长度N为1 000，L为500时，四种算法的计算复杂度依次为：乘法次数375 250、375 252、380 252、756 001；加法次数374 250、374 748、377 250、752 500。由此可知本文算法复杂度最低，M&M算法复杂度最高。

3 算法性能分析

通过仿真对上述讨论及算法进行了验证,并将本文算法与L&R算法、Fitz算法和M&M算法进行了比较。仿真使用了 AGWN下的 QPSK信号,即M=4。仿真中估计精度由归一化估计方差来衡量,简称为估计方差,定义为

AGWN下的QPSK信号，数据长度N为100，性噪比为10 dB，用MATLAB进行蒙托卡罗仿真实验，仿真结果如图2所示，其中图2(c)的纵坐标数量级为 10-3。从图中可以看出，本文算法和 M&M算法估计范围最大，归一化频偏范围可以近似得到0.5，验证了在本文第2节得到的结论。

算法的同步性能受信噪比的影响，因此本文在不同信噪比下进行仿真。图3是观察数据长度N=200,L=N/2=128,归一化频偏feT=0.002时,L&R算法、Fitz算法、M&M 算法和本文算法的估计方差随信噪比变化的曲线图,它反映了各算法在不同的信噪比下估计精度的变化趋势。

图2 频偏范围比较

图3 估计方差与信噪比的关系

由仿真图可以看出,在高信噪比条件下M&M算法的估计精度最高,新算法次之,L&R算法和Fitz算法的估计精度不及M&M算法和新算法。M&M算法虽然估计精度高,但是以较高的计算复杂度为代价。新算法在不同信噪比下的估计精度介于 M&M算法和L&R算法、Fitz算法之间,并且随着信噪比的增加,新算法估计精度接近于 M&M 算法,但是在低信噪比下,新算法的估计精度较低，仿真图3验证了理论分析中新算法估计精度较高的性能。

4 结语

本文利用相位折叠现象使得自相关函数的频偏具有周期化规律，基于这一思想,本文提出一种利用最大似然估计中的自相关函数进行频偏估计的算法,该算法估计范围广,精度高,且计算简单易于实现,适合短时突发信号传输模式,因此具有较高的实用价值,仿真结果也证明了算法的性能但是算法在低信噪比时估计精度较低,所以不适合在低信噪比情况下工作。

[1] PROAKIS J G. Digital Communications[M]. Fourth edition. Beijing: Publishing House of Electronics Industry,2006:333-372.

[2] RIFE D C, BOORSTYN R R. Single-tone Parameter Estimation from Discrete-time Observation[J].IEEE Trans Inform Theory,1974,20(05):591-598.

[3] KAY S. A Fast and Accurate Single Frequency Estimator[J].IEEE Trans Acoust Speech Signal Process, 1989,37(12):1987-1990.

[4] LUISE M, REGGINNAINI R. Carrier Frequency Recovery in All-digital Modems for Burst Mode Transmissions[J]. IEEE Transactions on Coieations,1995,43(02):1169-1178.

[5] FITZ M P. Further Results in the Fast Frequency Estimation of a Single Frequency[J].IEEE Trans.Comm, 1994, 42(04):862-864.

[6] MENGALI U, MORELLI M. Data-aided Frequency Estimation for Burst Digital Transmission [J].IEEE Trans. Comm, 1997, 45(01):23-25.

[7] 张电,高平,潘峰.网络协同取证系统的设计与实现[J].2011(07):89-91.

[8] 彭华.软件无线电中的盲接收技术研究[D].郑州:信息工程大学, 2001.

[9] 杜鹃,刘伟.超宽带通信系统中同步算法研究[J].通信技术,2010,43(09):35-38.

[10] 王俊,吴玉成,孟耘. 动态环境中频数字接收机载波同步研究[J].2010,43(01):66-68.

[11] 赵福才,胡以华,张立.卫星入路由通信的定时和载波同步算法[J].通信技术,2008,41(01):51-53.

[12] 王钢,刘毅鹏.BPSK载波同步技术的研究[J].通信技术,2003(02):21-22,33.

[13] 高翠东,赵琦,陆国雷.遥控副载波信号的软件解调方法[J].信息安全与通信保密,2009(12):50-52.

[14] 邱丹,张彬,许华.单频干扰对QPSK载波同步影响的分析[J].信息安全与通信保密,2005(06):104-106.