声纳浮标网络目标定位算法研究＊

周兆军

（海军702厂 上海 200434)

1 引言

声纳浮标网络是由大量的声纳浮标利用无线传感器网络（WSN)技术［1～3］组成的一个自组织网络系统。声纳浮标网络可用于对潜艇等水下目标进行定位，由于其利用多个节点相互协同，实现对目标的定位，因此其定位精度远远高于单个浮标定位精度。为了减少通信量，提高目标定位的实时性，声纳浮标往往只探测目标是否在自身探测范围内，所以其属于二元传感器，即传感器探测值只有0和1。所以声纳浮标网络属于二元传感器网络。

国内外对二元传感器网络目标定位与跟踪也进行了相应的研究［4～6］。文献［4～5］主要采用质心算法及加权质心算法来对目标进行定位。质心算法当传感器的探测范围较小时具有较好的性能，但当传感器的探测范围较大时，其性能大大降低。文献［5］的几种加权算法的权值都没有有效体现节点到目标的距离，因此精度不是很高。文献［6］提出了距离加权质心定位算法，使各个节点的权重有效体现了节点到目标的距离，提高了目标定位精度。但是各节点却需要传送额外的距离信息到融合中心，因此通信量增大，失去了二元传感器网络通信量小的优势。

本文针对文献［6］的不足，提出一种新的时间加权质心算法。算法将各节点探测的信号强度转换成节点发送探测信息的等待时间，利用等待时间的长短对各个节点位置进行加权，因此权重体现了各节点到目标的距离，提高了定位精度。由于不需要传送距离信息，因此通信量与质心算法相同。

2 问题描述

2.1 网络模型

WSN由N个声纳浮标节点组成，所有节点以均匀概率密度随机布设在网络监测区域内。假设每个节点都有唯一的标识且都知道自身的位置。每个浮标节点具有一定的无线通信距离C和探测距离R。其中，通信距离C由节点的无线通信功率决定，探测距离R由浮标节点的探测模型决定。在无线通信距离内，浮标节点之间可以通过无线方式进行通信，且每个节点都知道其邻居节点（距离小于通信距离)的位置。另外，浮标的通信距离C大于等于探测距离R的二倍，从而保证能够探测到目标的节点间都能够相互通信。最后，假设所有的浮标节点严格时间同步。

2.2 浮标探测模型

浮标节点探测目标的声音信号强度，并进行本地处理以得到节点的探测值。假设在时刻t，目标的位置为lt，节点s的位置为rs，则时刻t浮标节点s探测到的来自目标的信号强度［8～9］为

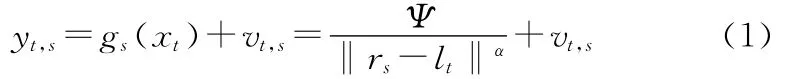
其中Ψ为单位距离上测得的来自目标的信号强度；‖rslt‖为rs和lt之间的欧几里德距离。α为损耗因子，它由信号的传播介质决定。可以认为它是一直不变的，并且对于所有浮标节点是相等的。vt，s为t时刻节点s接收到的噪声强度，当用于求平均能量的时间窗长度T足够长时，可以认为其服从于均值为uv、方差为σ2v的正态分布，即vt，s～N（uv，δ2v)。

节点在探测到来自目标的信号强度以后，在本地进行处理，并根据以下的规则决定其探测值。

1)节点将实际测得的信号强度与一个预定的阈值γ比较，如果测得的值小于γ，则其探测值为0。

2)如果测得的信号强度大于γ，则其探测值为1。

由上述模型的定义可得浮标节点的观测方程如下：

其中ys为节点测得的信号强度，可由式（1)得到。

在浮标节点获得探测值后，如果其探测值为0，则节点不向融合中心发送任何信息，以节省能量，如果探测值为1，则向融合中心发送信息。

3 时间加权质心算法

3.1 质心算法

质心算法的基本思想是：某一时刻如果有多个传感器节点探测到目标，则以这些探测到目标的节点的几何中心作为该时刻目标的位置。

3.2 距离加权质心算法

针对传统的质心算法和加权质心算法的不足，文献［6］提出了距离加权质心算法，其基本思想为：节点在测得目标信号强度后，根据传感器的探测模型，利用信号强度求出节点到目标的距离，然后将距离和探测信息一起发往融合中心，融合中心利用各节点到目标的距离对各节点的位置进行加权得到目标的位置。即如果某一时刻有S个节点探测到目标，其位置分别为（x1，y1)，（x2，y2)，…，（xS，yS)，且各节点到目标的距离分别为d1，d2，…，dS，则目标的位置为

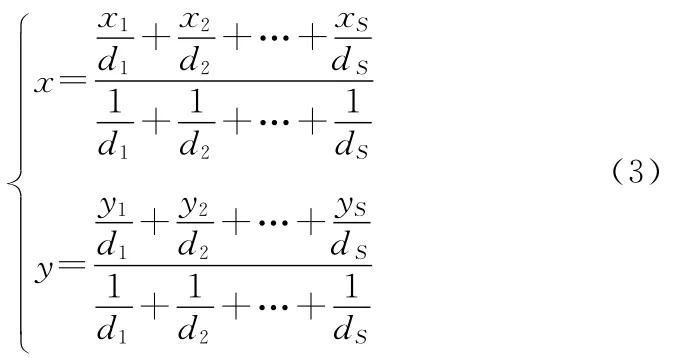
这种距离加权质心算法虽然使各个节点的权重有效体现了节点到目标的距离，提高了目标定位和跟踪精度。但是各节点却需要传送额外的距离信息到融合中心，因此通信量增大，失去了二元传感器网络通信量小的优势

3.3 时间加权质心算法

为了克服距离加权质心算法的不足，我们提出时间加权质心算法。其基本思想为：将各个节点探测到的信号强度转换成节点发送其探测信息的等待时间，从而每个探测到目标的节点发送信息的等待时间中就包含了节点到目标的距离，然后融合中心可以利用各节点的等待时间对各节点位置进行加权。下面进行详细介绍。

每一采样时刻，当浮标节点发现目标后，首先为该节点设置一等待时间ζs，当等待时间ζs结束后，节点再将探测信息传送给融合中心。其中ζs跟节点探测到的目标信号强度成反比，即ζs可以定义为

其中γ为探测阈值，ζmax为最大等待时间，由节点的采样间隔和目标速度决定。由于是单跳通信，因此通信时间很短，假设可以忽略不计。另外，由于所有节点是严格时间同步的，因此各节点传送探测信息的等待时间中就反映了该节点探测到的目标信号强度，从而也反映了该节点到目标的距离。因此，融合中心可以利用各节点发送信息的等待时间来对各节点的位置进行加权，在不增加通信量的情况下，提高质心算法的定位精度。

由浮标节点探测模型式（1)可得

故，式（3)的距离加权质心算法可以等价为时间加权质心算法：

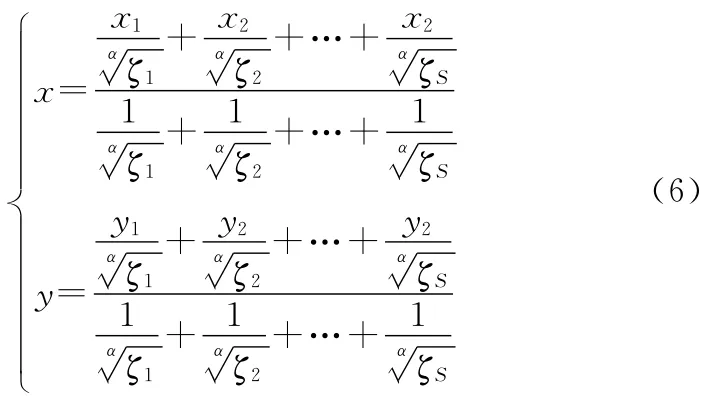
由于时间加权质心算法同样只传送节点的二元探测值到融合中心，因此其通信量与质心算法完全一样，不会增加额外的能耗。

4 计算机仿真分析

为了验证时间加权质心算法的有效性，利用Monte Carlo仿真［10～11］，将时间加权质心算法与质心算法的性能进行比较。仿真环境设置如下：

假设N个浮标节点以均匀概率密度随机布设在200×200m2的监测区域内，坐标原点设在网络覆盖区域的左下角。所有浮标节点的采样周期Tperiod＝1s，单位距离上测得的来自目标的信号强度Ψ＝1000，损耗因子α＝2，所有浮标节点的探测阈值为γ，系统状态噪声为Qw＝diag｛［0.01，0.01］｝，观测噪声均值为uv＝0，方差为δv＝0.09。

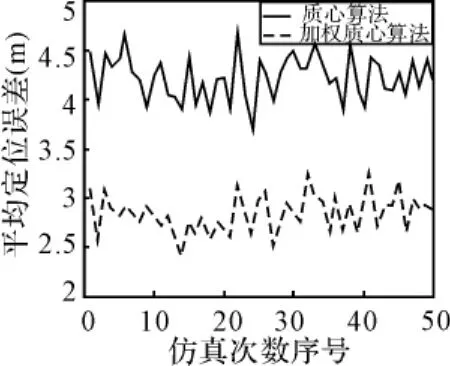
图1 两种算法定位精度比较

首先对算法的定位精度进行比较。仿真参数设置为：节点个数N＝400，探测阈值γ＝2。仿真50次，每次仿真中随机产生100个目标位置点，分别利用质心算法和时间加权质心算法对目标进行定位，并计算出每种定位方法的平均定位距离误差。仿真结果如图1所示。

从仿真结果可以看出，时间加权质心算法的平均定位误差明显小于质心算法的平均定位误差。以所有定位误差的均值来计算，时间加权质心算法相比质心算法定位精度可提高32.89%。

另外，为了验证节点个数N、节点探测阈值γ等参数对定位精度的影响，分别做了两次Monte Carlo仿真：1)假定节点探测阈值γ＝2，节点个数N从200变化到600，仿真结果如图2所示；2)假定节点个数为N＝400，节点探测阈值γ从2变化到5，仿真结果如图3所示。

图2 节点个数对定位精度的影响

图3 节点探测阈值γ对定位精度的影响

从仿真结果可以看出，质心算法和加权质心算法的定位误差都随着节点数目的增加而减小，而与探测阈值γ的关系不是很大。由于时间加权质心算法和质心算法的通信量完全相同，因此其能耗也与质心算法相同。

5 结语

声纳浮标网络可用于对潜艇等水下目标进行定位，因此其具有重要的军事应用价值。本文针对已有距离加权质心算法的不足，提出了一种新的时间加权质心定位算法，在通信量与质心算法一样的情况下提高了目标定位精度。新的时间加权质心算法将各个节点探测的信号强度转换成节点发送探测信息的等待时间，利用等待时间的长短对各个节点位置进行加权，因此权重体现了各节点到目标的距离，提高了目标定位与跟踪精度，而通信量与质心算法相同。仿真结果表明验证了算法的有效性。下一步我们将研究节点部署策略对定位跟踪精度的影响。

［1］CheeYee Chong，Kumar S P.Sensor networks：evolution，opportunities，and challenges［J］.Proc.of the IEEE，2003，91（8)：1247–1256.

［2］Li D，Wong K D，Hu Y H，et al.Detection，Classification，and Tracking of Targets［J］.IEEE Signal Processing Magazine，2002，19（2)：1729.

［3］Chong CY，Kumar S P.Sensor Netwoks：Evoltion，Opportunities，and Challenges［C］.Proceedings of the IEEE，2003，91（8)：12471256.

［4］Mechitov K，Sundresh S，Kwon Y，et al.Cooperative Tracking with Binary Detection Sensor Networks［C］.Proceedings of 1st International Conference on Embedded Networked Sensor Systems，2003：332333.

［5］Djuric P M，Vemula M，Bugallo M F.Target Tracking by Particle Filtering in Binary Sensor Networks［J］.IEEE Transactions on Signal Processing，2008，56（6)：22292238.

［6］孙晓艳，李建东，陈彦辉，等.二进制传感器网络加权目标跟踪算法研究［J］.电子与信息学报，2010，32（9)：20522057.

［7］彭燕.无线传感器网络定位优化算法及其仿真［J］.计算机与数字工程，2011（3).

［8］SHENG Xiao Hong，Hu YH.Maximum Likelihood Multiplesource Localization Using Acoustic Energy Measurements with Wireless Sensor Networks［J］.Transactions on Signal Processing，2005，53（1)：4453.

［9］Hu YH，SHENG Xiao Hong.Dynamc Sensor SelfOrganization for distributive Moving Target Tracking［J］.Journal of Signal Processing Systems，2008，51（1)：161171.

［10］Liu J S，Chen Rong.SequentialMonte Carlo Methods for Dynamic Systems［J］.Journal of Americal Statistical Association，1998，93（443)：10321044.

［11］Bortz A B.Kalos M H，Lebowitz J L.A new Algorithm for Monte Carlo Simulation of Ising Spin Systems［J］.Journal of Computational Physics，1975，17（1)：1018.