岩体结构面产状改进的K均值聚类分析

李继明

（义乌工商职业技术学院，浙江义乌 322000）

岩体结构面产状改进的K均值聚类分析

李继明

（义乌工商职业技术学院，浙江义乌 322000）

岩体结构面产状的优势分组是进行岩体工程稳定性评价的基础，极点等密度图、走向玫瑰花图等传统方法比较粗糙，只能给出优势组数，无法准确地给出每一组结构面的优势产状。为弥补传统方法的缺点，采用改进的K均值聚类算法，以结构面的单位法向量表示其产状，以结构面之间所夹锐角对结构面产状进行分类判定。将该方法应用于某采石场岩质边坡结构面优势产状的分析中，结果表明：采用改进的K均值聚类分析方法结果可靠，分类合理，可以准确确定结构面的优势产状。

岩体；结构面产状；优势分组；K均值聚类

1 研究背景

岩体中广泛地存在结构面，结构面的产状、密度及其组合规律对岩体的力学及水力学性质起着关键性的作用。要确保岩体工程的稳定性，首先要研究岩体结构面的分布规律，其基础性工作就是进行岩体的结构面统计，把统计的结构面按产状进行优势分组。

工程中最传统也是最常用的结构面优势分组方法是：画极点等密度图或走向玫瑰花图。其优点在于方法简便，可直观的判断优势组数；其缺点在于无法准确地确定优势产状，并且该方法具有很强的主观性，分组结果往往因各人的专业素养、经验的差异而不同［1］。Shanley和Mahtab［2］首次提出了结构面优势分组的客观聚类算法，该方法的难点在于确定寻找密度点时合理的小球半径。陈剑平等在文献［3］中对该方法进行了改进。Hammah和Curran［4］将模糊C均值聚类算法应用于结构面产状的优势组划分，该方法的难点在于确定有效的初始聚类中心。周玉新等［5］以模糊等价聚类方法得到的结果作为模糊软聚类方法的初始聚类中心，提出了结构面产状的综合聚类方法。蔡美峰等［6］提出了基于遗传算法的模糊C均值聚类算法。卢波等［1］提出了基于小生境Pareto遗传算法的优势组划分方法。范雷等［7］以结构面的单位法向量表示其产状，根据球面上2点之间的球面距离对结构面产状进行分类判定。

K均值聚类算法为聚类算法的一种，与模糊C均值算法一样，该方法的缺点在于必须确定合理的初始聚类中心。本文对K均值聚类算法进行改进，以结构面产状的凝聚点作为K均值聚类算法的初始聚类中心，而后对结构面产状进行优势分组。

2 数学描述及若干考虑

2.1 结构面产状的表达

在岩体结构面统计过程中，结构面产状通常用倾向（0°≤α＜360°）和倾角（0°≤β≤90°）表达。结构面为一空间平面，如图1所示建立空间直角坐标系，结构面产状可以用它单位法向量的坐标来表示［1，7］X＝（cosαsinβ，sinαsinβ，cosβ）。

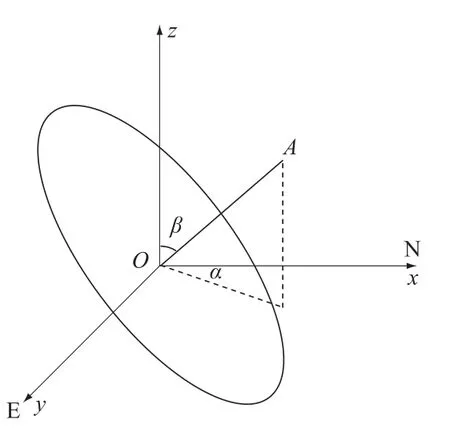
图1 结构面的空间表达Fig.1 Representation of discontinuity orientation

2.2 相似性度量

应用聚类算法对结构面的产状数据进行划分，首先需要确定结构面产状之间的相似性度量——距离［1］。本文以2结构面之间所夹的锐角作为相似性度量。设2个结构面为Xi和Xj，之间夹角为θ，根据2个向量之间的夹角公

式可以计算：

两结构面之间所夹锐角为

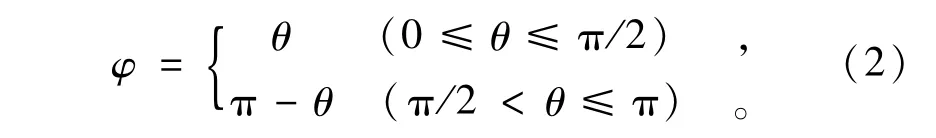
2.3 平均产状计算

结构面产状的划分是一个特殊的聚类问题，它存在陡倾角结构面的问题，即倾向相差约180°的陡倾角结构面产状是相似的，应归为一组。采用结构面之间的夹角作为相似性度量可解决此问题，但还存在另一问题，即平均产状的计算。本文用结构面的单位法向量表示其产状，平均单位法向量对应的结构面产状即为平均产状，但是当2结构面之间相差约180°时，所求的平均法向量是错误的。需做如下处理计算平均法向量：如图2所示，先计算其中一个法向量关于圆心的镜像向量，然后计算这个镜像向量与另一个法向量的平均向量。至于将哪一个法向量做镜像，取决于计算出的平均向量要指向z轴的正向。

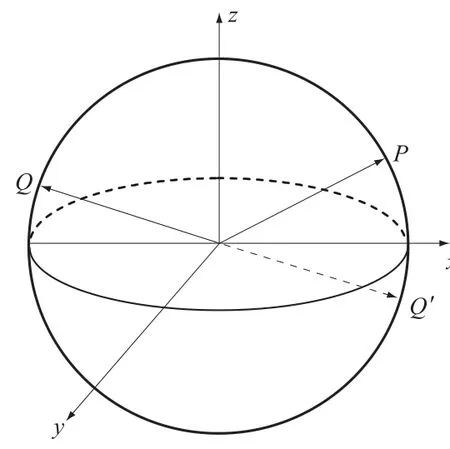
图2 平均产状计算示意图Fig.2 Calculation ofmean vectors

2.4 分组数的确定

通常情况下，结构面产状的分组数完全可以在野外结构面统计过程中确定下来。极点等密度图和玫瑰花图也是判断结构面优势组数直观有效的方法。当分组数完全不确定的情况下，可假设分组数为2到8，分组之后通过聚类效果的有效性检验确定最优的分组数，文［8］中有详细介绍。分组数的确定不是本文讨论的重点，本文假设分组数已知情况下，应用改进的K均值聚类算法进行结构面产状的划分，并确定优势产状。

3 改进的K均值聚类算法

3.1 确定初始聚类中心

应用K均值聚类算法首先要确定初始聚类中心。此算法对于初始聚类中心的敏感性较强，初始聚类中心的选择直接影响着聚类结果的正确性，因此，聚类中心的选择必须合理。在介绍如何确定合理的聚类中心的方法之前，提出一个概念，即：

密度点数ρ为距离某一结构面Xi，夹角小于角度半径R的结构面的个数，即为此结构面对应半径R的密度点数。给定一个角度半径R，假设在所有N个结构面中与结构面Xi夹角小于R的结构面共有m个，则结构面Xi对应半径R的密度点数就是m。

下面介绍合理的聚类中心的确定方法：

（1）给定一较小的半径R，分别计算N个结构面的密度点数ρ，找出密度点数最大的结构面。

（2）增大半径R，重复步骤（1）。

（3）重复步骤（2）若干次。

（4）完成第（3）步之后，分别找出了对应不同的半径R的密度点数最大的结构面。其中必然存在某一结构面出现不止一次，确定出现次数最多的结构面产状，此结构面产状即为一个聚类中心μ1。

（5）将以第（4）步中结构面的产状为中心，半径为π／2K内的结构面剔除。K为已知的分组数。

（6）重复以上步骤K－1此，确定其余K－1个聚类中心μ2，μ3，…，μK。

3.2 K均值聚类算法

确定了合理的聚类中心之后，采用K均值聚类算法对结构面产状数据进行优势分组，详细过程如下［9］：

（2）确定每个结构面的分组。分别计算N个结构面到K个聚类中心的距离，假设一个结构面到第i个结构面最近，则它属于第i组。

以上过程简单，很容易编程实现，本文使用matlab将上述过程程序化，用于结构面产状的优势分组。

4 实例分析

某采石场一岩质边坡，呈北东向展布，坡长约73 m，坡角83°，岩性主要为花岗岩。岩体中节理、裂隙发育，岩石被切割成块状，边坡局部有滑痕，存在潜在危险。根据现场调查岩体发育4组结构面，现场统计195个结构面，极点图见图3。应用改进的K均值聚类算法对其进行优势组划分。分组结果见表1，图4为分组极点图，分组结果清晰可靠，为进一步进行边坡稳定性的评价提供了可靠依据。

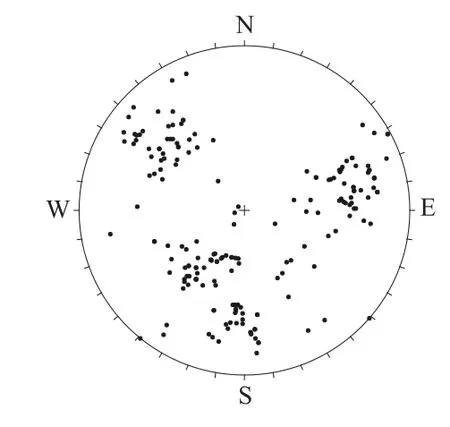
图3 结构面极点图Fig.3 Polemap of discontinuities

图4 分组结构面极点图Fig.4 Polemap of cluster results

表1 分组结果Table1 Clustering results

5 结 语

K均值聚类算法的缺陷在于，聚类结果对初始聚类中心的敏感性较大，必须首先确定合理的聚类中心。本文对其进行改进，将结构面产状的凝聚点作为K均值聚类算法的初始聚类中心，而后对结构面产状数据进行优势分组。理论和实例分析表明，应用改进的K均值聚类算法研究岩体结构面产状的分布规律，分类结果准确，分类更加合理。此方法可以弥补等密度图、玫瑰花图等传统方法的不足，可以准确地给出每一组结构面的个数，并可以精确地给出每一组面的优势产状。

结构面产状的改进K均值聚类算法，原理简单，操作方便，分类结果准确可靠，可为进一步进行岩体的稳定性评价和结构面网络数值模拟提供可靠依据，此方法具有重要的实用意义。

［1］ 卢 波，丁秀丽，邬爱清.岩体随机不连续面产状数据划分方法研究［J］.岩石力学与工程学报，2007，26（9）：1809－1816.（LU Bo，DING Xiu-li，WU Ai-qing.Study on Method of Orientation Data Partitioning of Random ly Distributed Discontinuities of Rocks［J］.Chinese Journal of Rock Mechanics and Engineering，2007，26（9）：1809－1816.（in Chinese））

［2］ SHANLEY R J，MAHTAB M A.Delineation and Analysis of Clusters in Orientation Data［J］.Mathematical Geology，1976，8（3）：9－23.

［3］ 陈剑平，石丙飞，王 清.工程岩体随机结构面优势方向的表示法初探［J］.岩石力学与工程学报，2005，24（2）：241－245.（CHEN Jian-ping，SHIBing-fei，WANG Qing.Study on the Dominant Orientations of Random Fractures of Fractured Rock Masses［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24（2）：241－245.（in Chinese））

［4］ HAMMAH R E，CURRAN JH.Fuzzy Cluster Algorithm for the Automatic Delineation of Joint Sets［J］.International Journal of Rock Mechanics and Mining Sciences，1998，35（7）：889－905.

［5］ 周玉新，周志芳，孙其国.岩体结构面产状的综合模糊聚类分析［J］.岩石力学与工程学报，2005，24（13）：2283－2287.（ZHOU Yu-xin，ZHOU Zhi-fang，SUN Qiguo.Synthetic Fuzzy Clustering Analysis for Joints Occurrence of Rock Mass［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24（13）：2283－2287.（in Chinese））

［6］ 蔡美峰，王 鹏，赵 奎，等.基于遗传算法的岩体结构面的模糊C均值聚类方法［J］.岩石力学与工程学报，2005，24（3）：371－376.（CAI Mei-feng，WANG Peng，ZHAO Kui，et al.Fuzzy C-Means Cluster Analysis Based on Genetic Algorithm for Automatic Identification of Joint Sets［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24（3）：371－376.（in Chinese））

［7］ 范 雷，王亮清，唐辉明.节理岩体结构面产状的动态聚类分析［J］.岩土力学，2007，28（11）：2405－2408.（FAN Lei，WANG Liang-qing，TANG Hui-ming.Dynamic Cluster Analysis of Orientations of Jointed Rock Mass［J］.Rock and Soil Mechanics，2007，28（11）：2405－2408.（in Chinese））

［8］ HAMMAH R E，CURRAN JH.Validity Measures for the Fuzzy Cluster Analysis of Orientations［J］.Pattern Analysis and Machine Intelligence，2000，12（22）：1467－1472.

［9］ 张建辉.K-means聚类算法研究及应用［D］.武汉：武汉理工大学，2007.（ZHANG Jian-hui.Research and Application of K-Means Clustering Algorithm［D］.Wuhan：Wuhan University of Technology，2007.（in Chinese） ）

（编辑：姜小兰）

Im proved K-M eans Clustering Analysis on Discontinuity Orientations of Rock M ass

LIJi-ming
（Yiwu Industrial＆Commercial College，Yiwu 322000，China）

The analysis of dominant orientations of discontinuities is a fundamental work for a further evaluation of the stability of rockmass.By traditional plotmethods such as isopycnic diagram and rose diagram，we can only obtain a simple classification of the orientations，but the exact dominant orientations of every set cannot be acquired.An improved K-means clustering algorithm is proposed.The orientations of discontinuities are represented by their unit normal vectors，and the included acute angle between two discontinuities is taken as their similaritymeasure.Data investigated from a rock slope of a quarry is used as a case study.The results of K-means clustering algorithm are reliable and reasonable.Thismethod can give the accurate dominant orientations of every set.

rock mass；discontinuity；dominant orientation；K -means clustering

TU452

A

1001－5485（2012）09－0049－04

10.3969／j.issn.1001－5485.2012.09.012

2012－03－12；

2012－04－18

李继明（1967－），男，甘肃天水人，副教授，高级工程师，主要从事岩土工程、建筑工程管理方面的研究，（电话）13777512198（电子信箱）lijimingzzz＠163.com。