沱江上游径流周期性与季节影响分析

于芷婧，郝颖坤

（四川大学a.水利水电学院；b.数学学院，成都 610065）

沱江上游径流周期性与季节影响分析

于芷婧a，郝颖坤b

（四川大学a.水利水电学院；b.数学学院，成都 610065）

依据沱江上游三皇庙水文站近50 a的流量资料，采用小波分析方法对多年月径流量与各年汛期流量进行多时间尺度的周期性分析和突变点检验。通过小波方差图得到各序列变化的主周期；尝试应用X－11季节调整方法对月流量序列进行季节因子提取，分析得到月径流量的多年变化走势和季节影响特点。结果表明：月流量存在3个突出的主周期，分别为1～2，11，21 a，此外还有3 a和5 a两个不明显周期；汛期流量则表现明显为3，5，13 a的3个主周期；每年的汛期月流量季节因子影响明显高于整体水平，受季节因素影响显著，其中7月份季节影响因子呈逐年增大，年际变化平稳，8，9月季节影响因子年际变化剧烈。

小波分析；突变点；小波方差；主周期；X－11季节调整法；季节因子

沱江为长江上游的一级支流，位于中国四川省中部。沱江上游地区属四川盆地气候区，集水面积6 590 km2，其洪水主要由上游龙门山暴雨带暴雨形成，暴雨集中在6—9月，年降水量1 200～1 600 mm，沱江上游洪水属典型天然河道洪水特性，通过历史洪水系列分析，排除人为干扰因素［1］。了解与掌握长江上游径流的变化特性与演变规律有助于长江流域水资源的开发利用和渠灌区水资源的优化调度。

本文采用沱江上游三皇庙水文站近50 a的流量数据，利用复Morlet小波变换对月流量和逐年汛期流量进行多尺度分析，并采用小波方差对分析结果进行检验。在小波分析结论的基础上引入X－11季节调整方法对月径流量序列进行季节因子提取，以寻求其整体变化趋势和季节因子影响特点。

1 小波分析

小波分析方法是20世纪80年代初发展起来的一种信号时、频局部化分析的新方法，它在时域和频域上同时具有良好的局部化功能，可以对时间序列进行局部化分析，剖析其内部精细结构，因此小波分析十分有利于研究水文系统的多时间尺度变换特征［2－3］。

1.1 小波理论

对于给定的小波函数Ψ（t），水文时间序列f（t）∈L2（R）的连续小波变换公式为

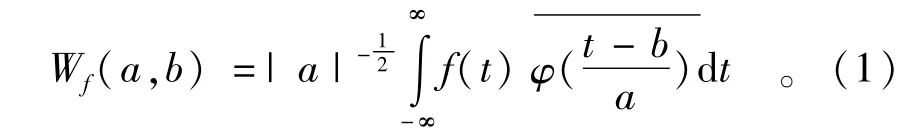
式中：Wf（a，b）为小波变换系数；a为尺度因子，反映小波的周期长度，在一定意义上1／a对应于频率¯ω；b为时间因子，反映时间上的平移；基小波为复共轭函数。实际应用中，水文时间序列常为（1）式的离散形式如（2）式：

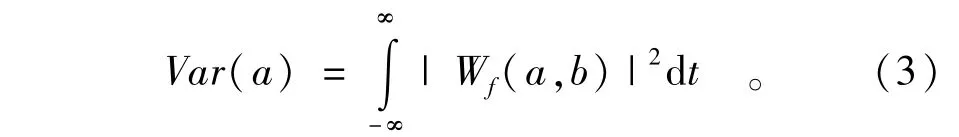
小波方差随时间尺度a变化的关系图叫做小波方差图。小波方差图反映波动能量在时间域的分布。因此通过小波方差图可以确定水文序列中存在的主周期，用来衡量小波分析结果的可靠性。

1.2 资料处理

本文采用三皇庙水文站1941—1986年共46 a的流量资料。资料整理得到逐月流量x1（t）（t＝1，2，3，

式中：k＝1，2，3，…，N，为离散点数；Δt为取样时间间隔；f（kΔt）为水文时间序列。

对小波系数平方在时间域上的积分即得到小波方差：…，552）和逐年汛期（6—9月）平均流量序列x2（t）（t＝1，2，3，…，46）。为方便计算，减少序列噪声的影响，对月均流量与汛期平均流量序列分别进行中心化处理得到平距序列x′1（t）和x′2（t），即x′i（t）＝式中为序列均值，σ为序列标准差，

i＝1，2。鉴于复数小波比实型小波能更真实地反映变量在各时间尺度上周期性的大小及这些周期在时域中的分布，本文采用复Morlet小波对资料序列进行变换。将Morlet小波函数φ（t）＝代入上述

（2）式中，经过计算得到序列在该小波变换下的小波系数，绘制小波系数时频分布图，进行结果分析。

1.3 结果分析

复数小波变换系数的模和实部是2个重要的变量。模的大小表示特征时间尺度信号的强弱，实部可表示不同特征时间尺度信号在不同时间的强弱和位相2方面的信息［3］。小波变换系数的实部包含给定时间和尺度下，相对于其它时间和尺度，信号的强度和位相2方面的信息，为正时表示径流量偏多，为负时表示径流量偏少，为零时对应着突变点。

图1清晰显示了三皇庙水文站月径流量小波系数的三维时频分布图，底部投影图（图2）反映的是小波系数实部在不同时间尺度下的变化特征。图3为年汛期流量距平序列小波系数实部时频分布图。依据小波变换系数在时间域内不同尺度下的分布情况，可以清晰分辨出月径流量和汛期流量的时间尺度特性、突变点位置及其相位结构。2序列都具有明显的多时间特性，各大中尺度震荡中还嵌套着较小尺度的周期震荡。其中月径流序列在1～2 a的年内震荡较为明显，正负相位交替出现，波动极值点分布规律，反映的是年内的洪枯季节变化特性。10～13 a间的时间尺度下震荡尤为明显，中心周期在11 a左右，多水少水年组交替出现。突变点大致在1946，1953，1960，1967，1974，1981年，其中1946—1953，1960—1967，1974—1981年各时段为正相位，各月水量偏多；1946年之前，1953—1960，1967—1974，1881—1986年各时段为负相位，水量偏少。更大范围上的21 a时间尺度的周期性变化也比较明显，正负相位交替出现。对于汛期径流小波系数时频图进行分析可得：各年汛期流量较明显的时间尺度为13 a左右，其突变点大致分布在1946，1952—1953，1974，1979年，各年份间丰枯水相间，此分析结果与月径流量在11 a尺度下的丰枯突变年份大致相同，反映月流量与汛期流量在此时间尺度上的丰枯同步性，符合一般规律。另外，汛期流量在3 a与5 a两个时间尺度下，小波系数也具有周期性正负出现的特征。

图1 月径流量小波系数变换时频分布Fig.1 Three-dimensional time-frequency distribution of wavelet coefficients ofmonthly runoff

图2 月径流量小波系数二维等值图Fig.2 Two-dimensional contour diagram of wavelet coefficients ofmonthly runoff

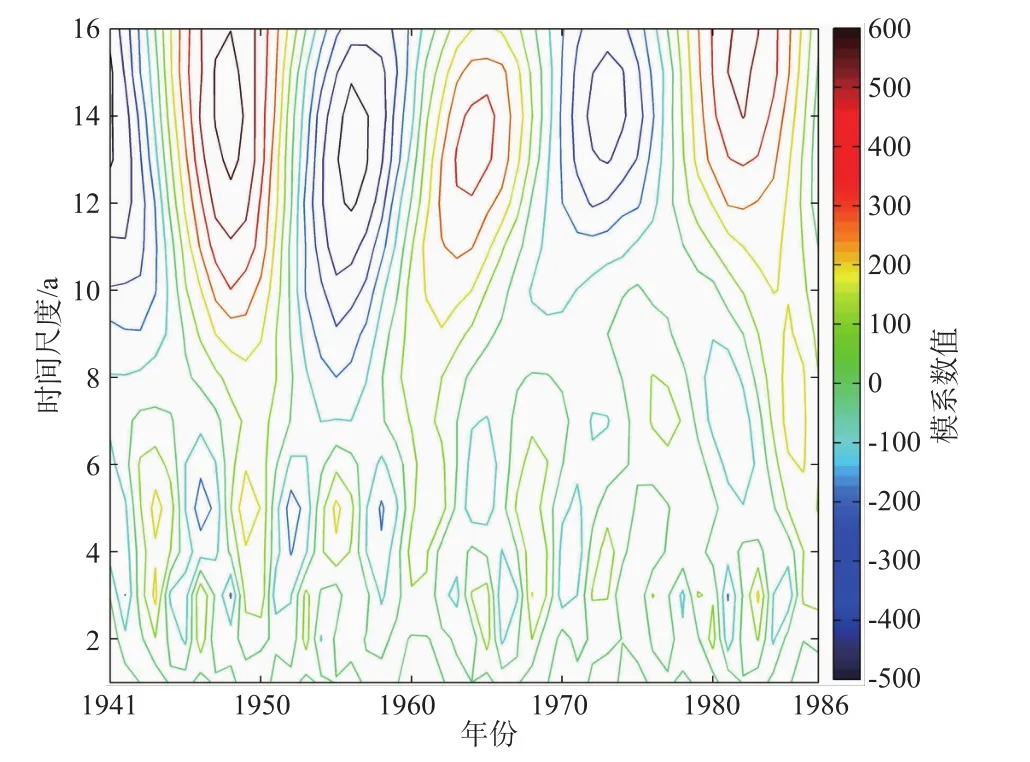
图3 年汛期流量距平序列小波变化系数实部时频分布Fig.3 Real part time-frequency distribution of wavelet coefficients of runoff in flood season

1.4 小波方差检验

根据小波方差概念，分别计算月均流量与年汛期流量的各时间尺度对应的小波方差，并绘制方差时间尺度关系图（图4、图5）。从图中可以清晰地分辨出月流量与汛期流量的主周期。其中，月径流量方差图存在3个突出的主周期，分别为1～2，11，21 a，此外还有3 a和5 a两个弱周期。年汛期流量表现明显为3，5，13 a的3个主周期，其中13 a左右的周期震荡最为强烈。

图4 月径流小波方差图Fig.4 Wavelet variogram of themonthly runoff

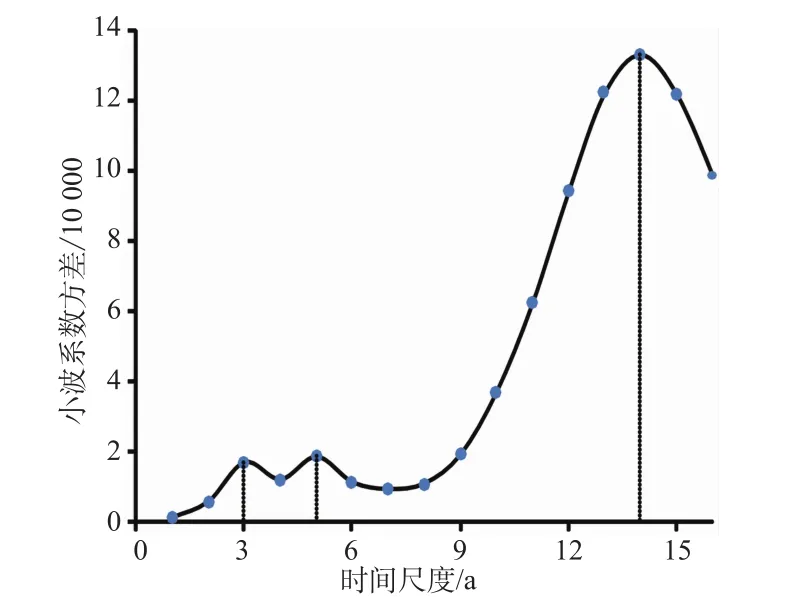
图5 汛期流量方差图Fig.5 Wavelet variogram of the runoff series in flood season

2 X－11季节调整

X－11过程是由美国国情调查局于1965年编制的时间序列季节调整过程。X－11过程能够很好地对时间序列中的季节影响因素进行提取。它的基本原理是时间序列的确定性因素分解法。X－11过程是基于这样的假定：任何时间序列都可以拆分成长期趋势起伏Tt、季节波动St、不规则波动It的影响。X－11过程在反映时间序列长期趋势起伏规律中效用显著，在分析月径流序列的季节特性基础上，试进行X－11过程趋势模拟。

2.1 X－11过程原理

X－11过程中普遍采用移动平均的方法：用多次短期中心移动消除随机波动，用周期移动平均消除趋势，用特征量周期移动平均消除季节因素影响。在整个过程中，总共要用到11次移动平均，因此得名。

2.2 趋势模拟

基于SAS平台，应用pro x11语句编程得到模拟程序。将月径流序列输入程序中，对逐年累月流量过程变化趋势进行模拟。依据X－11过程原理，以所得残差序列为白噪声序列为模型优良评定标准。对模拟结果所得残差进行白噪声序列的假设检验。假设残差为白噪声，经计算P值为0.343 6＞0.05，无法拒绝原假设，既得残差为白噪声序列，证明趋势拟合效果较为良好，说明X－11过程用作年径流趋势模拟可以得到较为理想的效果。

2.3 趋势与季节因子分析

依据所得趋势经过分析得到各年月流量年际变化趋势。在较小的时间尺度范围内，逐年之间的径流变化波动较大，各年份间径流量起伏变化不定。在较大的时间范围内，图像清晰显示着1941—1946年年径流量整体呈下降趋势，1946—1953年呈上升趋势，而1953年之后至1960年年径流下降比较明显。1960—1968年年径流量震动较为剧烈，整体略显下降，但趋势不明显，1969—1977年整体趋势上升，随后的几年径流量呈小幅度震荡，直到1984年之后呈明显下降趋势。在更大范围尺度上，1960—1961年年径流量发生陡增外，径流量整体呈现递减趋势。

分析由X－11过程得到的46 a各月季节因子均值（图6），季节影响因子在汛期7—9月数值明显大于整体水平，反映出汛期流量受季节影响尤为显著，变化复杂。分析汛期各月季节影响因子的逐年变化趋势（图7）不难看出，各年7月份的季节影响因子呈逐年上升趋势，各年间变化幅度较为平缓；相比之下，8月与9月季节影响因子波动剧烈，逐年变差较大。

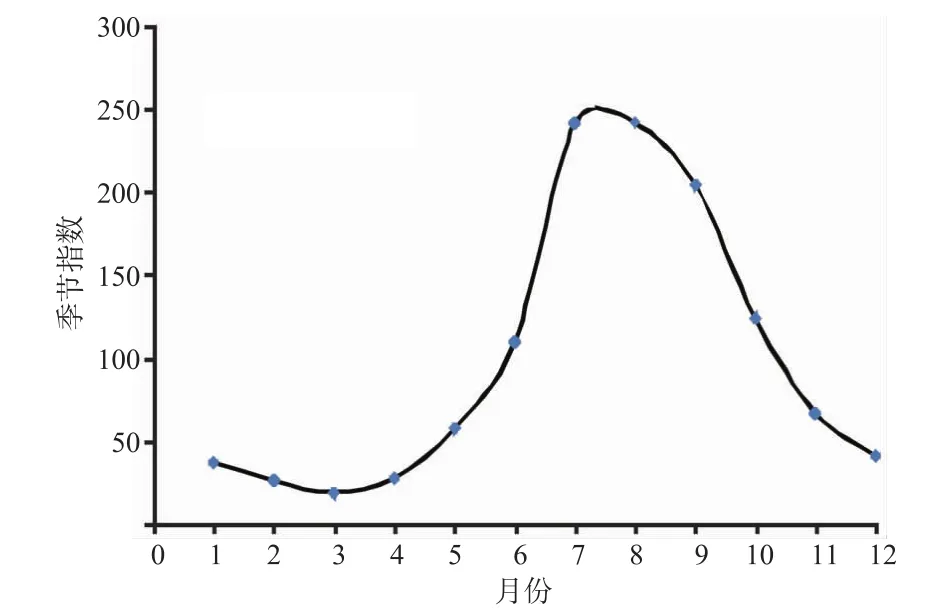
图6 各月季节因子分布图Fig.6 Distribution ofmonthly seasonal factors

图7 汛期各月影响因子变化趋势Fig.7 Trend of seasonal factors in flood seasons

2.4 讨 论

应用X－11过程模拟得到的年径流量的整体变化趋势中，其中趋势转折点分别出现在1946，1953，1960，1968，1984年，此结果与采用小波分析在时间尺度为11 a的突变点预测结果十分相近。同时，从趋势分析图（图7）中也可以清晰地反映突变点两侧水量的多少相间分布。2种不同角度的分析方法得到了相类似的结论，不仅验证了分析结果的可靠性，同时说明X－11季节调整方法在水文特征量趋势模拟中可以取得比较好的结果。

3 结 论

（1）沱江上游月径流量与汛期流量呈现多时间尺度变化特征，各种时间尺度在时域上分布不均匀；时间尺度不同，月径流量与汛期流量所处的丰枯阶段不同，在大尺度的周期震荡中同时嵌套着许多小尺度下的周期变化。

（2）径流量在10～13 a间的时间尺度下震荡明显，中心周期在11 a左右，突变点大致在1946，1953，1960，1967，1974，1981年，突变间年份多水少水年组交替出现；汛期流量较明显的时间尺度为13 a左右，其突变点大致分布在1946，1952—1953，1974，1979年，各年份间丰枯相间。

（3）经小波方差分析，月流量存在3个突出的主周期，分别为1～2，11，21 a，此外还有3 a和5 a两个弱周期；汛期流量则表现明显为3，5，13 a的3个主周期。

（4）应用X－11季节调整方法对月流量时间序列变化趋势进行模拟，得到不错的效果，较为清晰地反映了流量的逐年增减变化趋势。分析逐年季节因子得到，每年的汛期月流量季节因子影响明显高于整体水平，受季节因素影响显著。其中7月份季节影响因子呈逐年增大，年际变化平稳，8，9两月季节影响因子年际变化剧烈。

［1］ 吴玉明.沱江上游长期洪水预报初探［J］.水文，2003，23（4）：27－28.（WU Yu-ming.Preliminary Study on the Long-term Flood for the Upper Reach of Tuojiang River［J］.Hydrology，2003，23（4）：27－28.（in Chinese））

［2］ 张少文，丁 晶，廖 杰，等.基于小波的黄河上游天然年径流变化特性分析［J］.四川大学学报：工程科学版，2004，（3）：32－37.（ZHANG Shao-wen，DING Jing，LIAO Jie，et al.Analysis of Natural Annual Flow Time Series in the Upper Reach of the Yellow River Based on Wavelet Transform［J］.Journal of Sichuan U-niversity：Engineering Science Edition，2004，（3）：32－37.（in Chinese））

［3］ 王文圣，丁 晶，李跃清.水文小波分析［M］.北京：化学工业出版社，2005.（WANG Wen-sheng，DING Jing，LIYue-qing.Hydrological Wavelet Analysis［M］.Beijing：Chemical Industry Press，2005.（in Chinese））

［4］ 胡安焱，郭生练，陈 华，等.基于小波变换的汉江径流量多时间尺度分析［J］.人民长江，2006，（11）：61－62.（HU An-yan，GUO Sheng-lian，CHEN Hua，et al.Multi-time Scales Analysis of the Flow in the Hanjiang River Based on Wavelet Transform［J］.Yangtze River，2006，（11）：61－62.（in Chinese））

［5］ 安 全，梁 川，刘 政.雅砻江中上游径流变化特性的小波分析［J］.武汉大学学报，2008，（6）：20－24.（AN Quan，LIANG Chuan，LIU Zheng.Wavelet Analysis of Runoff Variation Characteristics in Upper Middle Reaches of Yalong River［J］.Journal ofWuhan University，2008，（6）：20－24.（in Chinese））

［6］ 刘仕国.关于时序数据的季节调整、季度变化率与年度变化率的推导及年度化方法［J］.世界经济统计研究，2003，（1）：15－21.（LIU Shi-guo.Annualized Method and Deduction of Seasonal Adjustment，Quarterly rate，Annual Rate about the Time Series［J］.TheWorld Economic Statistical Studies，2003，（1）：15－21.（in Chinese））

［7］ 高惠璇.SAS系统·SAS／ETS软件使用手册［M］.北京：中国统计出版社，1998.（GAO Hui-xuan.Manual of SASSystem·SAS／ETS Software［M］.Beijing：China Statistics Press，1998.（in Chinese） ）

（编辑：赵卫兵）

Periodic and Seasonal Impact of Runoff in the Upstream of Tuojiang River

YU Zhi-jing1，HAO Ying-kun2
（1.College ofWater Resource and Hydropower，Sichuan University，Chengdu 610065，China；2.College of Mathematics，Sichuan University，Chengdu 610065，China）

Based on runoff series in the past50 yearsmeasured at Sanhuangmiao hydrologic station in the upstream of Tuojiang River，we adopted wavelet analysis to analyze themonthly runoff over years and the flood season flow in each year to find out the catastrophe points and period characteristics atmulti-time scales.Wavelet variogram was used to identify dominant periods，and X-11 seasonal adjustmentmethod was applied to extract the seasonal factors from monthly runoff series in order to obtain the trend and the seasonal impact.Results indicated that：themonthly runoff series exhibited three dominant periods of1-2 years，11 years，and 21 years and two sub-dominant periods of 3 years and 5 years，while the flood season flow was featured by three obvious dominant periods of3 years，5 years，and 13 years.The impact of seasonal factors on monthly runoff in flood seasons were higher than that in other months.The seasonal factors in July increased steadily by years，and changed remarkably in August and September.Researches on runoff changewould contribute to the exploitation ofwater resources and the optimal scheduling ofwater resources in canal irrigation areas.

wavelet analysis；catastrophe points；wavelet variance；dominant periods；X-11seasonal adjustment；seasonal factors

P333

A

1001－5485（2012）09－0005－04

10.3969／j.issn.1001－5485.2012.09.002

2011－06－20；

2011－07－15

于芷婧（1989－），女，辽宁鞍山人，本科，主要从事水文水资源方面的研究，（电话）18811363463（电子信箱）1020687893＠qq.com。