公路隧道地震响应计算的拟静力法

杨林德，隋 涛，刘 鹏

（同济大学a.地下建筑与工程系，上海 200092；b.建设综合勘察研究设计院有限公司，北京 100007）

公路隧道地震响应计算的拟静力法

杨林德a，b，隋 涛a，b，刘 鹏a，b

（同济大学a.地下建筑与工程系，上海 200092；b.建设综合勘察研究设计院有限公司，北京 100007）

鉴于对公路隧道抗震计算的简化算法迄今研究尚少，提出了一种适用于公路隧道地震响应计算的拟静力法。以Ⅳ级围岩中的双车道公路隧道为例，通过将衬砌结构视为弹性地基上的框架结构，将结构承受的水平地震力简化为作用在结构单元结点上的等效水平集中力，侧向地基弹性抗力假设为按倒三角形分布，墙底为零，拱顶为最大值，其值按与水平等效地震力平衡的原则确定。通过比选确定水平地震作用修正系数η的取值，即可由结构静力分析得到与结构动力响应分布图形相似、最大值十分接近的等效弯矩图，其相应的最大轴力值和最大剪力值，可通过由结构静力分析得到的内力图结果分别乘以轴力、剪力调整系数获得。提出的方法可供工程设计及公路隧道地震响应进一步研究参考。

公路隧道；地震响应；抗震设计；拟静力法

1 研究背景

阪神地震之前，人们普遍认为地下结构具有较强的抗震能力，阪神地震之后，人们才意识到强震作用下地下结构也会发生严重的破坏。我国西部地区很多已建和在建的公路隧道集中在地震高发和高烈度区，2008年的汶川地震使其当地许多公路隧道遭受不同程度的破坏［1－2］，给震后抢修及修复带来困难。因此，对公路隧道的抗震设防能力加强研究有较大的意义。

目前，公路隧道的抗震计算方法有时程分析法、圆形结构动力响应解析解和拟静力法等。其中时程分析法有普遍适用性，但因计算过程较为繁琐而不受设计人员欢迎，解析解仅适用于圆形隧道。拟静力法通常受到欢迎，但现有方法源自铁路隧道的设计规范，没有考虑公路隧道断面形状、尺寸等与铁路隧道的差异对动力响应的影响。鉴于公路隧道抗震能力的评估已日益受到重视，对其抗震设计计算研究建立更为合理的拟静力法很有意义。

本文以双车道直墙拱形公路隧道为例，根据对衬砌结构采用时程分析法进行地震响应计算得到的结果，对其建立计算地震响应的拟静力法。

2 基本原理

地震响应分析中，结构体系的动力平衡微分方程可表示为［3－4］

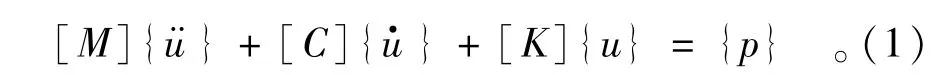
式中：［M］，［C］，［K］分别为体系的质量矩阵、阻尼矩阵及刚度矩阵，｛u¨｝，和｛u｝分别为体系的加速度向量、速度向量和位移向量列阵，｛p｝为荷载向量列阵。

地震响应分析的算法，本文采用了基于有限差分的显式时程分析算法。

采用拟静力法计算时，拟将隧道结构承受的水平地震力简化为作用在结构单元结点上的等效水平集中力F，其值按式（2）确定。

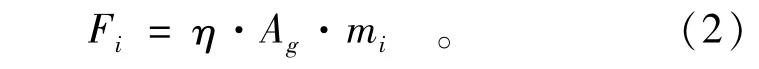
式中：Fi为作用在结构单元结点i上的等效水平地震力（N）；η为水平地震作用修正系数；Ag为设计基本地震加速度（m／s2）；mi为通过结构单元结点i的各个构件的质量之半的总和（kg）。

隧道衬砌结构可视为底部弹性地基上的框架结构，侧墙与底板的连接方式分别假设为铰接和固结，侧向地基弹性抗力假设按倒三角形分布，墙底为零，拱顶为最大值，其值按与水平向等效地震力平衡的原则确定，如图1所示。

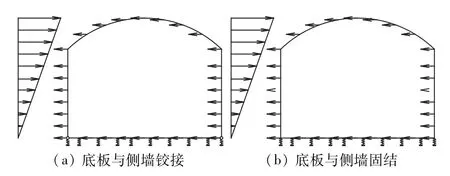
图1 等效水平地震荷载分布图Fig.1 Distribution of equivalent horizontal seism ic load

研究表明按图1计算时，结构最大动内力的分布规律与由时程分析算法得到的结果相符，最大动内力值则可拟按极限作用效应相等的原则，通过合理确定水平地震作用修正系数η值，使拟静力计算的结构内力与动力时程分析法计算的结构内力接近。

此外，鉴于隧道结构地震动力响应的特征参数最大弯矩、最大轴力和最大剪力不能同时达到最大值，等效地震荷载拟按使主要构件的最大动弯矩值相等的原则确定。同时对其余构件的最大动弯矩及各构件的最大动轴力和最大动剪力，通过引入调整系数修正。

3 拟静力法的水平地震作用修正系数

以某双车道公路隧道为例。设某双车道公路隧道（图2）净跨10.8 m，净高8.4 m。初喷混凝土厚0.15 m，二衬混凝土厚0.4 m，底板厚0.4 m。隧道埋深为80 m。地层均匀，围岩级别为Ⅳ级，弹性模量为3.700 MPa，泊松比为0.33，密度为2 200 kg／m3，弹性抗力系数为250 MPa／m。初喷混凝土标号C20，密度为2 300 kg／m3，弹性模量为25 000MPa，泊松比为0.2；二衬混凝土标号C25，密度为2 500 kg／m3，弹性模量为29 500 MPa，泊松比为0.2。

3.1 动力问题分析

影响地下结构动力响应计算结果的因素有计算范围、岩土介质的动力特性、边界条件及地震波输入等。杨林德、季倩倩等［5～8］通过对上海软土地铁车站结构进行振动台模型试验研究，提出了进行地下结构地震响应计算的成套方法，本文予以参考。

3.1.1 计算区域

本算例中，计算区域选为125 m×139 m，见图3。在隧道左右两侧为对称布置，每侧自边墙外侧起算的宽度均达到隧道跨度的5倍。下部厚度超过隧道高度的5倍，上部边界取至地表，并也超过隧道高度的5倍。

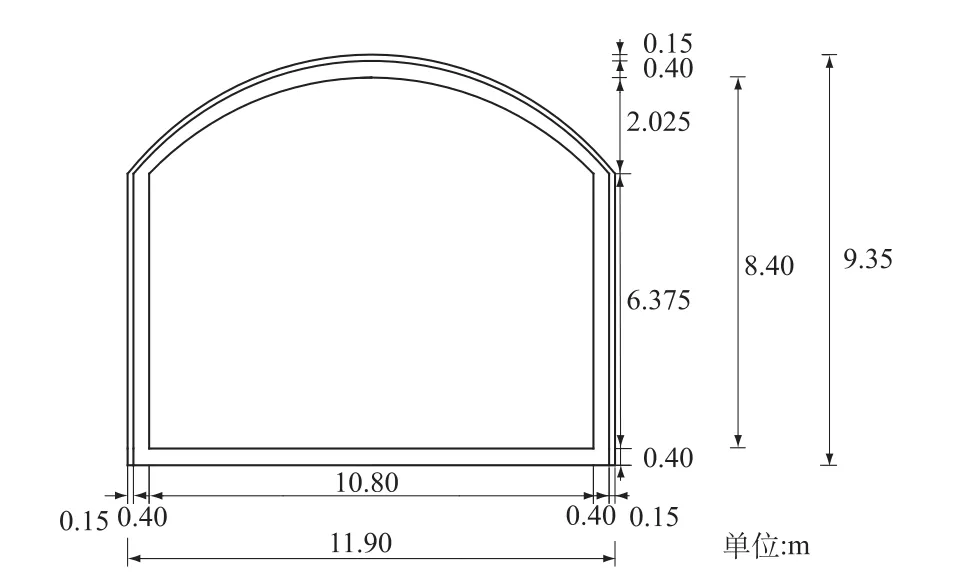
图2 双线公路隧道衬砌断面图（Ⅳ级围岩）Fig.2 Sectional draw ing of the lining tunnel of double-lane highway（rock gradeⅣ）

3.1.2 单元划分

采用有限差分法计算时，岩体地层采用平面四边形单元划分网格，结构采用梁单元离散。形成的网格共6 512个结点，6 351个平面四边形单元，38个梁单元，如图4所示。图5为隧道结构单元离散放大图。

图3 动力时程法计算范围图Fig.3 Calculation range of dynam ic time-history method

图4 动力时程法计算网格图Fig.4 Calculation meshes of dynam ic time-history method

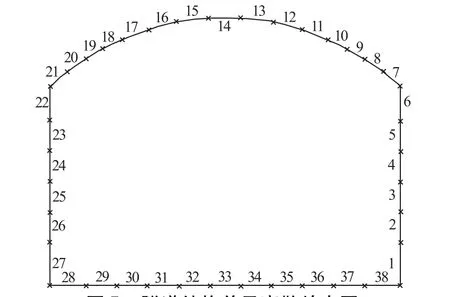
图5 隧道结构单元离散放大图Fig.5 Enlargement draw ing of discrete tunnel structural elements

3.1.3 边界条件

两侧边界选为自由场边界，其底部边界竖向固定、水平向自由，顶部为无约束自由边界。

3.1.4 地震动输入

根据结构周围场地的条件以及抗震设防的要求来确定地震动输入加速度峰值的大小。基岩处输入的地震加速度为地表面的1／2，基岩至地表按深度线性内插［9］。本文拟采用设计基准期为50 a，超越概率为10%的kobe地震波输入。其峰值加速度按设防烈度7度进行调幅，即地表的设计基本地震加速度值为0.1 g，输入的地震加速度值为0.05 g，相应的地震加速度时程曲线见图6。

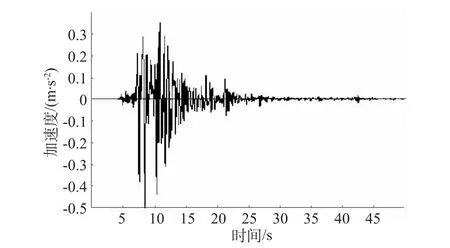
图6 计算范围底部输入的地震波加速度时程曲线图Fig.6 Time-history curve of the input seism ic wave acceleration at the bottom of calculation range

3.1.5 计算工况

本项计算主要研究隧道衬砌的动内力，结构侧墙与底板的连接按铰接和固结计算。

3.1.6 计算结果

何谓小说家？毕飞宇有个有趣的说法，他说小说家就是身体倍儿棒的人，他的眼力好，旁人能看厘米，他能看毫米；旁人能听十米，他能听一里；旁人能辨五味，他能辨千滋百味。他说的是莫言，是作家那超人的感受力。不过，黄金明并不是莫言式的作家，他不是那种用身体写作的人，他是用思想写作的小说家。他没有用耳目口鼻让世界变得五光十色、五味杂陈万花筒般旋转起来，但他始终探索一种必须用宏大的思想坐标和敏锐的心智结构才能理解的先锋性十足的智性小说。

通过计算得到了双车道公路隧道结构的动内力见图7、图8。其中侧墙与底板为铰接时，隧道结构的最大动弯矩、动轴力和动剪力图分别见图7（a），7（b），7（c）；侧墙与底板为固结时，相应的最大动弯矩、动轴力和动剪力图分别见图8（a），8（b），8（c）。

图7 侧墙与底板铰接隧道结构最大动内力图Fig.7 Themaximum dynam ic internal forces of the tunnel when sidewall and bottom are hinged

图8 侧墙与底板固结隧道结构最大动内力图Fig.8 Themaximum dynam ic internal forces of the tunnelwhen sidewall and bottom are consolidated

由以上内力图可见，当假设侧墙与底板铰接时，隧道结构的最大动弯矩值发生在拱脚、墙顶相交处，其值为44.637 kN·m。而当假设侧墙与底板固结时，最大动弯矩值发生在侧墙与底板相交处，其值为61.856 kN·m，拱脚处的最大动弯矩为44.152 kN·m。

3.2 拟静力法的计算

3.2.1 单元划分

如图9所示，隧道结构采用平面梁单元离散，底部弹性地基的作用采用弹簧模拟。共有38个结点，38个梁单元。其中拱圈划分为15个单元，左右侧墙各6个单元，底板11个单元。

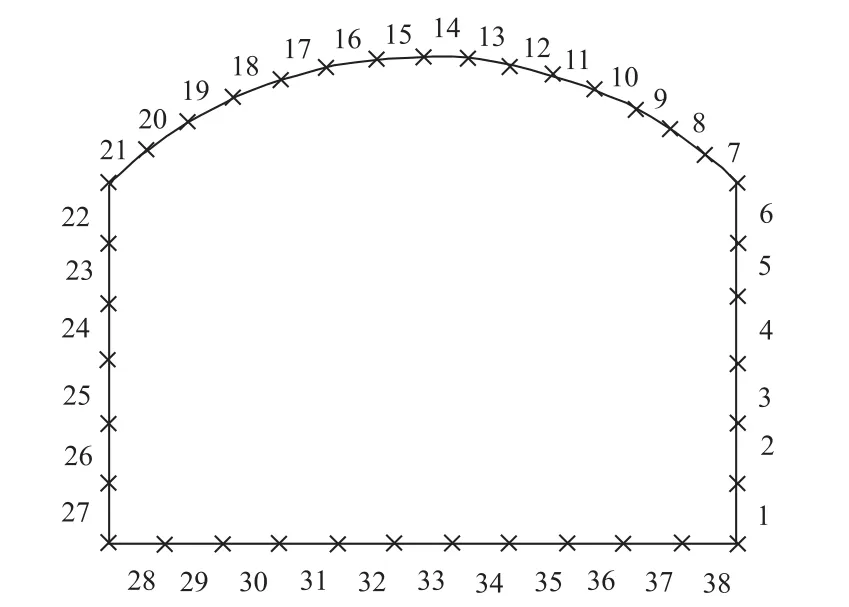
图9 隧道结构计算单元图（拟静力法）Fig.9 Calculation element of tunnel structure（quasi-static m ethod）

隧道结构侧墙与底板的连接，仍按铰接和固结分别计算。

3.2.2 荷载

3.2.3 计算结果

按拟静力法计算得到的与隧道结构的动力响应等效的内力图见10、图11。其中图10为假设侧墙与底板铰接时，隧道结构的等效弯矩图（10（a））、轴力图（10（b））和剪力图（10（c））；图11为假设侧墙与底板固结时隧道结构的等效弯矩图（11（a））、轴力图（11（b））和剪力图（11（c））。

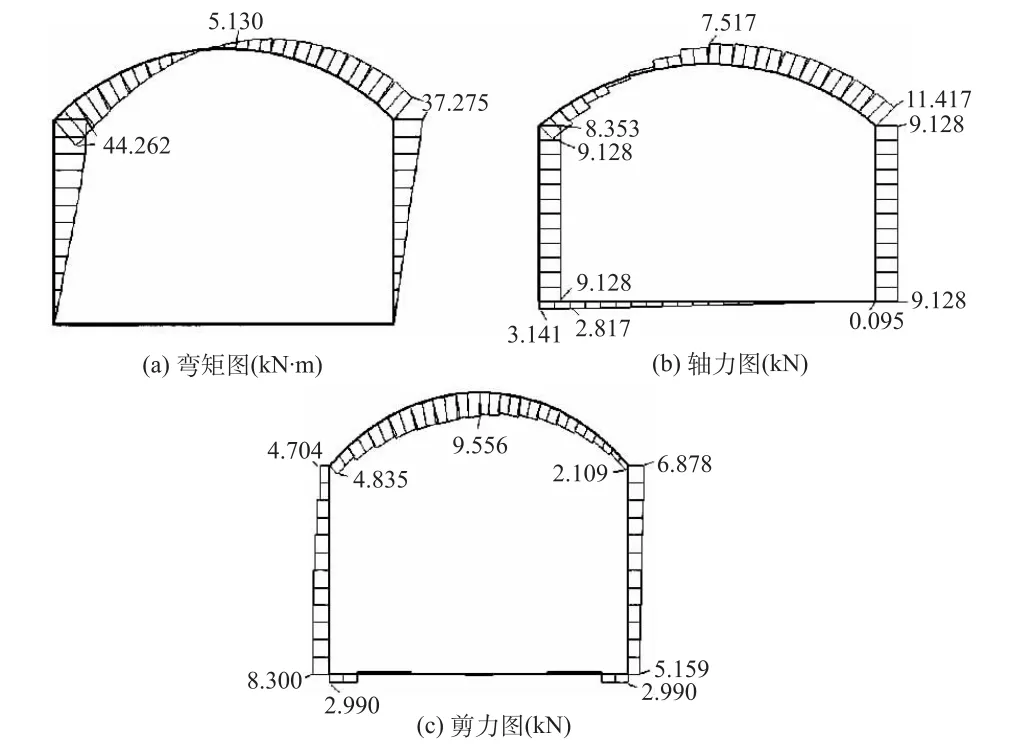
图10 侧墙与底板铰接隧道结构的动力响应等效内力图（η＝0.32）Fig.10 Internal forces equivalent to the dynam ic response of tunnel structure when sidewall and bottom are hinged（η＝0.32）

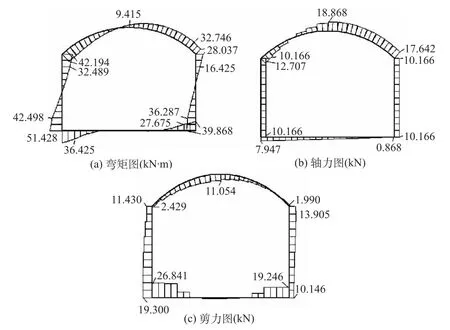
图11 侧墙与底板固结隧道结构的动力响应等效内力图（η＝0.70）Fig.11 Internal forces equivalent to the dynam ic response of tunnel structure when sidewall and bottom are consolidated（η＝0.70）

由以上内力图可见，当假设侧墙与底板铰接，且水平地震作用修正系数η＝0.32时，隧道结构的最大等效弯矩值也发生在拱脚、墙顶相交处，其值为44.262 kN·m，与动力时程分析结果的误差仅为1%；当假设侧墙与底板固接，且水平地震作用修正系数η＝0.70，隧道结构的等效最大弯矩值仍发生在左右侧墙与底板相交处，其大小为51.428 kN·m，与动力时程分析法的误差为17%，但拱脚处的弯矩值为42.194 kN·m，与动力时程分析法的误差仅为4%。鉴于拱墙相交截面常是结构承载力检验的控制截面，故可认为符合极限作用效应相等的原则。

3.3 系数η的取值

在图1、图2的计算假定下，经对Ⅳ级围岩下双线公路隧道按不同η值进行对比计算分析，可知假设隧道结构的侧墙与底板铰接时，水平地震作用修正系数的合理取值范围为η＝0.20～0.40；而假设隧道结构的侧墙与底板固结时，则其合理取值范围为η＝0.60～0.80。

与此同时，假设侧墙与底板为铰接或固结时，隧道结构拱脚处的最大等效轴力、剪力值将与最大动轴力、动剪力值都相差甚大。为了得到隧道结构的最大等效轴力、剪力值，需将由拟静力法计算得到的轴力和剪力值分别乘以轴力调整系数α（α＝动轴力／静轴力）和剪力调整系数β（β＝动剪力／静剪力）。研究表明如按拱脚截面内力值最大计，假设隧道结构的侧墙与底板铰接，η＝0.20～0.40时，轴力调整系数的取值范围为α＝70～35，剪力调整系数的取值范围为β＝20～10；假设隧道结构的侧墙与底板固结，η＝0.60～0.80时，轴力调整系数的取值范围为α＝40～20，剪力调整系数的取值范围为β＝30～20。

4 结 语

本文以Ⅳ级围岩中的双车道公路隧道为例，提出一种可用于对其进行地震动力响应计算的拟静力法。

研究表明通过将隧道衬砌结构视为底部弹性地基上的框架结构，结构承受的水平地震力简化为作用在结构单元结点上的等效水平集中力，及将侧向地基弹性抗力假设为按倒三角形分布，墙底为零，拱顶为最大值，其值按与水平向等效地震力平衡的原则确定，则可在通过比选确定水平地震作用修正系数η的取值后，由结构静力分析得到与动力响应内力分布图形相似、最大值十分接近的等效弯矩图。其相应的等效轴力、剪力值，可通过乘以轴力、剪力调整系数获得。鉴于对公路隧道抗震计算的简化算法迄今研究尚少，文中提出的方法可为工程设计和进一步的公路隧道地震响应研究提供参考。

［1］ 王明年，崔光耀，林国进.汶川地震灾区公路隧道震害调查及初步分析［J］.西南公路，2009，（4）：41－46.（WANG Ming-nian，CUIGuang-yao，LIN Guo-jin.Investigation and Preliminary Analysis of Damages on Road Tunnel in Wenchuan Earthquake Areas［J］.Southwest Highway，2009，（4）：41－46.（in Chinese））

［2］ 高 波，王峥峥，袁 松，等.汶川地震公路隧道震害启示［J］.西南交通大学学报，2009，44（3）：336－341.（GAO Bo，WANG Zheng-zheng，YUAN Song，et al.Lessons Learnt from Damage of Highway Tunnels in Wenchuan Earthquake［J］.Journal of Southwest Jiaotong University，2009，44（3）：336－341.（in Chinese））

［3］ 谢康和，周 健.岩土工程有限元分析理论与应用［M］.北京：科学出版社，2002.（XIE Kang-he，ZHOU Jian.Theory and Application of Rock-Soil Finite Element Analysis［M］.Beijing：Science Press，2002.（in Chinese））

［4］ 周 健，徐 冰，徐建平.土动力学理论与计算［M］.北京：中国建筑工业出版社，2001.（ZHOU Jian，XU Bing，XU Jian-ping.Theories and Calculations of Soil Dynamics［M］.Beijing：China Architecture＆Building Press，2001.（in Chinese））

［5］ 杨林德，杨 超，季倩倩，等.地铁车站的振动台试验与地震响应的计算方法［J］.同济大学学报，2003，31（10）：1135－1140.（YANG Lin-de，YANG Chao，JI Qian-qian，et al.Shaking Table Test and Numerical Calculation on Subway Station Structures in Soft Soil［J］.Journal of Tongji University，2003，31（10）：1135－1140.（in Chinese））

［6］ 杨林德，季倩倩，郑永来，等.地铁车站结构振动台试验中模型箱设计的研究［J］.岩土工程学报，2004，26（1）：75－78.（YANG Lin-de，JI qian-qian，ZHENG Yong-lai，et al.Study on Design of Test Box in Shaking Table Test for Subway Station Structure Station Structure in Soft Soil［J］.Chinese Journal of Geotechnical Engineering，2004，26（1）：75－78.（in Chinese））

［7］ 杨林德，王国波，郑永来，等.地铁车站接头结构振动台模型试验及地震响应的三维数值模拟［J］.岩土工程学报，2007，29（12）：1892－1898.（YANG Lin-de，WANG Guo-bo，ZHENG Yong-lai，et al.Shaking Table Tests on Subway Station Joint Structure and 3D Numerical Simulation of Seismic Response［J］.Chinese Journal of Geotechnical Engineering，2007，29（12）：1892－1898.（in Chinese））

［8］ 季倩倩.地铁车站结构振动台模型试验研究［D］.上海：同济大学地下建筑与工程系，2002.（JIQian-qian.Model Test on Shaker Table of Subway Station Structure［D］.Shanghai：Department of Geotechnical Engineering of Tongji University，2002.（in Chinese））

［9］ GB50011—2010，建筑抗震设计规范［S］.（GB50011—2010，Code for Seismic Design of Buildings［S］.（in Chinese） ）

（编辑：姜小兰）

Quasi-static Calculation M ethod of Seism ic Response of Highway Tunnel

YANG Lin-de1，2，SUITao1，2，LIU Peng1，2
（1.Department of Geotechnical Engineering，Tongji University，Shanghai 200092，China；2.China Institute of Geotechnical Investigation and Surveying Ltd.，Tongji University，Beijing 100007，China）

Rare researches were focused on the simplified method of aseismic calculation for highway tunnels.A quasi-static calculation of the seismic response of highway tunnel is proposed.In this method，the tunnel lining structure is regarded as frame structure on elastic foundation，and the horizontal seismic force on the structure is simplified as equivalent horizontal concentrated force on element nodes of the structure.The lateral elastic resistance is assumed to be distributed in an inverted triangle，which is zero at the bottom of the wall and reaches the maximum at the vault.The value of lateral elastic resistance should be in balancewith horizontal equivalent seismic force.A double-lane highway tunnelwith rock of gradeⅣis taken as a case study.Through comparison and selection，the value of correction coefficientηof the horizontal seismic action is determined.Hence，through static structural analysis，the equivalentbendingmoment diagram is obtained，which is similar to the distribution graph of dynamic analysis，with themaximum values close to each other.The correspondingmaximum axial force andmaximum shear force can be obtained through respectivelymultiplying the adjustment coefficient of axial force and shear force by the internal force resulted from the static structural analysis.Themethod could be taken as a reference for engineering design and further research.

highway tunnel；seismic response；aseismic design；quasi-static method

U452

A

1001－5485（2012）09－0059－05

10.3969／j.issn.1001－5485.2012.09.014

2012－02－15；

2012－05－10

深部岩土力学与地下工程国家重点实验室开放基金（SKLGDUEK1011）

杨林德（1939－），男，江苏无锡人，教授，博士生导师，主要从事地下建筑结构抗震防灾减灾研究，（电话）021－68983982（电子信箱）tjyanglinde＠163.com。

隋 涛（1982－），男，陕西渭南人，博士研究生，主要从事地下建筑结构抗震防灾减灾研究，（电话）021－65985142（电子信箱）suitao654com＠163.com。