均匀介质目标高阶矩量法的高效预处理方法

伍月千 盛新庆

（北京理工大学信息与电子学院电磁仿真中心，北京100081）

引 言

对于介质体散射的研究具有极其重要的理论意义和应用价值，例如很多实际物体的电磁散射都可近似成介质体的散射。当介质体为均匀介质时，基于面积分方程的矩量法，因其高效性和精确性成为解决均匀介质体散射问题的最有效的方法之一。近年来为了进一步提高矩量法的性能与仿真能力，高阶矩量法技术以其精确、高效的特性被广泛应用［1－4］。高阶矩量法包括几何形状高阶模拟与基函数高阶模拟两部分。对于表面弯曲的目标，用高阶曲面元能显著提高几何模拟的精度，可以用更少的面元逼近实际目标，从而减少剖分单元的个数；而高阶基函数的应用，提高了高阶面元上等效源的模拟精度，从而获得更高的计算精度和更高效的计算效率。

表述均匀介质体的面积分方程有很多种形式。研究表明：基于不同形式的矩量法的计算精度、稳定性以及效率都各不相同［5－6］。数值实验表明CTF方程以其高精度和稳定性好被广泛采用。但是CTF方程与高阶矩量法结合后会使矩阵条件数增大，矩阵性态变差，导致迭代步数增多甚至出现不收敛的情况。因此，利用有效的预条件技术加速其迭代求解速度是高阶矩量法实现的一个关键。

对于面积分方程的预处理方法，Levent Gürel等［6－7］应用块对角预处理（BP）以及近似多项式预处理提高低阶矩量法的迭代收敛速度。通过研究CTF离散方程的矩阵特性，发现矩阵方程中等效电流和等效磁流的两个耦合项具有绝对数值相差很大的特征。根据此特性，将电流与磁流耦合项中弱耦合作用项略去。然后，采用不完全 LU（ILUT）［8－9］计算所需求解的矩阵逆。为了检验提出的高效预处理方法对高阶矩量法离散CTF方程的作用，我们分别计算了介质球体、介质立方体等目标。计算结果表明了文中所提预处理的高阶CTF方程的高效性与精确性。同时，数值实验还表明：与BP相比，文中所提预处理技术的构造时间与其相当，但由于考虑了电流与磁流间的耦合作用，提高收敛速度效果更佳。最后，为了表现预处理高阶CTF方程的计算能力，计算了电尺寸达10个波长的电大介质球。

1 理论分析

1.1 介质体目标的高阶CTF方程

考虑如图1所示的均匀介质体目标在平面波入射下的散射（S为介质体的边界，取等效面为介质体边界）。由等效原理可知：等效面对应的等效源为（J，M），介质体内或外的电磁场满足电场积分方程（EFIE－I或 EFIE－O）和磁场积分方程（MFIE－I或MFIE－O）.

图1 三维均匀介质体目标散射示意图

将内外电场方程、内外磁场方程分别用以下方式组合

取a＝b＝c＝d＝1，便可得到CTF方程

式中：Ei（r）、Hi（r）表示入射电场和磁场；Zl为介质l的波阻抗；L与K算子定义为

为了更方便从形式上研究CTF方程的矩阵性态，将介质体表面的等效电流与等效磁流分为两个子区域，取基函数Bn和试函数Tm为相同形式，从而对式（3），（4）的系数矩阵A进行如下分块

其中矩阵元素表示为

从式（7）可以得到如下结论：CTF方程中的L算子部分所对应的离散矩阵为主对角占优矩阵，且完全对称；QTE的数值量级相对于其他三块分块矩阵偏小，以计算直径为λ0的介质球（ε＝2）的电磁散射为例，λ0为自由空间波长，QTE的数量级为10－4到10－5，PTH的数量级为100到10－1，PTE的数量级为10－1到10－2；同时与K算子相比，L算子没有涉及奇异点残留项，故CTF方程具有更高的计算精度。对于L算子中奇异项计算使用改进型Duffy变换来消除奇异点［10］，使精度进一步提高。选取高阶基函数Bn与试函数Tm将主对角元素PTE展开为

式中，L1，L2，L′1，L′2为参考坐标系。

高阶矩量法包含高阶面片和高阶基函数两个方面，前者是几何模型的高阶几何逼近，后者是电流分布的高阶逼近。由于三角形的灵活性和通用性，选取剖分面元为曲边三角形。高阶基函数分为插值型基函数和叠加型基函数，相对于插值型高阶基函数，叠加型高阶基函数具有如下优势：向低阶基函数兼容的性质，不要求整个网格上采用相同阶数的基函数；网格阶数与基函数的阶数完全独立，使得网格和基函数的阶数选取更灵活［11－13］。但由于叠加型基函数之间不具有正交性，通常得到的矩阵条件数相对较差，故对其进行了正交化［13－14］，并采用预处理技术改进矩阵的条件数。

1.2 预处理矩阵的构造

CTF方程最终形成的系数矩阵A，因矩阵条件数偏大，导致收敛效果不佳。因此，需要对其采用一些高效的预处理技术。一般来说，预处理器的构造过程中，将涉及到矩阵逆的求解。在此，我们选用一类带双丢弃门限的ILU分解算法ILUT，该算法通过设置丢弃门限和设定预条件矩阵每行最多保留元素个数，有效地控制计算预条件矩阵所花费的时间。同时，预处理矩阵的存储量不会有明显改变。在ILUT分解的基础上，针对CTF离散方程的系数矩阵特点，构造出预处理矩阵。

首先对系数矩阵A按等效电流和等效磁流分割为分块矩阵，根据高阶CTF方程系数矩阵的性质将矩阵A分解得到近似矩阵M，得到预处理矩阵M－1.

所提预处理器的构造过程为：对矩阵A进行分块，应用矩阵主对角对称的性质（PTE＝QTH），以及QTE数值量级极小的性质忽略其耦合作用（QTE≈0），得到矩阵A的近似矩阵M 为

再将M分解为

于是便可得到矩阵A的预处理矩阵为

从上面所述构建过程可以看出：在构建的过程中，利用主对角块矩阵完全相同的性质可以将构造预处理的时间，也即ILUT求近似逆的时间减少一半，与BP预处理器构造时间相同，只需求 （PTE）－1；同时根据矩阵特点，进一步忽略耦合作用极小的分块矩阵QTE，则进一步减少了每一步迭代中的矩阵向量乘积的时间，实现了高效化；与BP相对比，文中所提预处理技术不仅考虑了主对角矩阵的作用，更是结合了等效电流和等效磁流的耦合作用，最大程度上保留了矩阵A的有用信息，因此，具有更好的预处理加速效果。

2 实验结果分析

为验证文中所提预处理技术的高效性与精确性，计算了几种介质目标的雷达散射截面。以下算例的雷达散射截面（RCS）均为在300MHz均匀平面电磁波照射下的计算结果，高阶基函数采用1.5阶叠加型基函数，用广义最小残差（GMRES）迭代器求解，收敛门限设置为10－3.为了更好地对比数值计算结果雷达散射截面（RCS）的精度，在此引入均方根误差（RMS），σcal和σref分别为计算值和解析值，RMS定义为

验证高阶叠加型基函数求解介质体问题的准确性。算例为直径为3λ0的介质球，介电常数为2，图2展示了分别采用0.5阶、1.5阶基函数计算此介质球的RCS与Mie值的对比。其中，0.5阶基函数用细网格剖分，剖分的平均边长约为0.07λ0，未知数个数为37 248，数值解与解析解的均方根误差为0.110 9；高阶基函数用粗网格剖分，剖分的平均边长为0.3λ0，未知数个数为6 420，其对应的方均根误差为0.078 8.显然，叠加型高阶基函数仅用RWG基函数1/6的未知数就得到了更高的计算精度。

研究文中所提预处理方法在各种情况下的加速效果。首先是目标电尺寸变化对预处理效果的影响。计算了相同介电常数，相同剖分但不同尺寸的介质球目标。在此计算中，介质球的直径分别为3λ0、5λ0，剖分的平均边长均为0.3λ0，未知数个数分别为6 480和20 480，介电常数为2.分别用无预处理、BP以及文中所提预处理技术所需计算时间，迭代步数以及内存如表1和表2所示。

图2 直径为3λ0的介质球双站雷达散射截面（θinc＝0°）

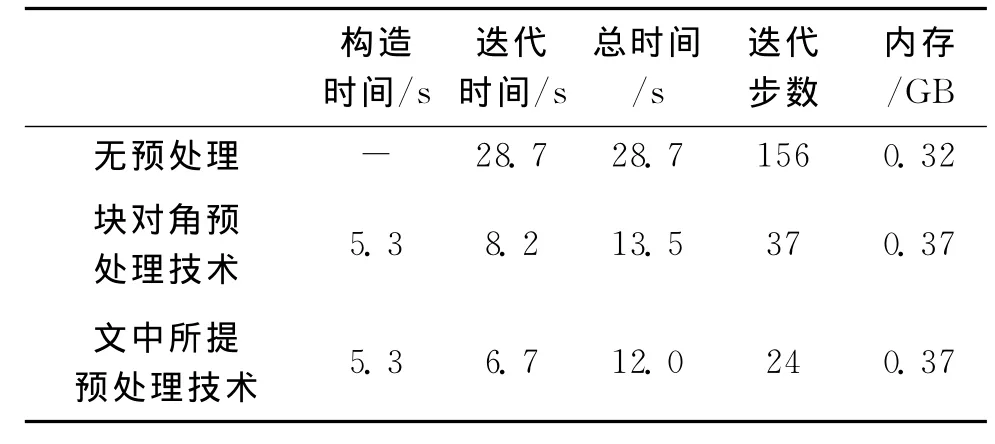
表1 直径为3λ0的介质球（ε＝2）无预处理，BP与文中所提预处理技术所需计算资源比较

表2 直径为5λ0的介质球（ε＝2）无预处理，BP与文中所提预处理技术所需计算资源比较

由两表可知：随着半径的增加，未知数增多，计算所需总的时间增多；通过迭代时间和迭代步数的对比，文中所提预处理技术和BP明显优于无预处理的GMRES求解，特别是应用文中所提预处理技术使得迭代步数最少，分别为原来的1/6，1/10，总时间减少为不用预处理所需总时间的1/2，1/3.随着半径增加，矩阵向量相乘所需时间的增加将远远大于预处理器构造时间的增加，此时，采用预处理减少迭代步数所带来的优势更加明显。

考虑介质参数的变化对预处理效果的影响。计算相同尺寸，相同剖分，不同介电常数的介质球的散射。固定介质球直径为4λ0，剖分尺寸为0.3λ0，未知数个数为13 520，介电常数分别为2和3.采用无预处理，BP以及文中所提预处理技术所需要的计算时间，迭代步数以及内存见表3和表4所示。通过表3和表4可以看出：随着介电常数的增大，总体迭代步数随之增加；与无预处理相比，BP和文中所提预处理技术优势明显；相比于BP，文中所提预处理技术的效果更好，优势更为明显；随着介电常数的增加，文中所提预处理效果达到4倍以上。

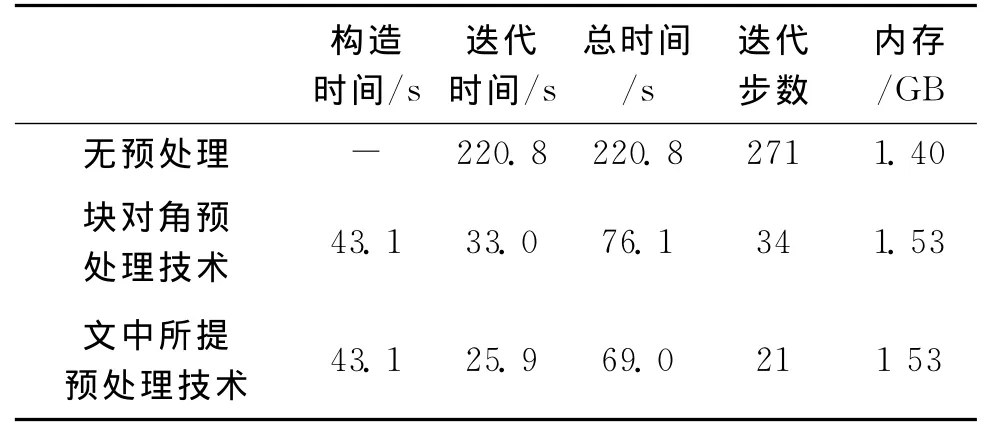
表3 直径为4λ0的介质球（ε＝2）无预处理，BP与文中所提预处理技术所需计算资源比较

表4 直径为4λ0的介质球（ε＝3）无预处理，BP与文中所提预处理技术所需计算资源比较

为了进一步比较目标形状变化对两种预处理效果的影响，我们计算了边长为4λ0的介质立方体，介电常数为4，剖分尺寸为 0.3λ0，未知数个数为25 960.采用无预处理求解、BP以及文中所提预处理技术所需要的计算时间、迭代步数以及内存见表5，对迭代步数与所需总体时间分析的结论与前面各算例结果一致，这再一次说明了两种预处理方法的高效性，同时体现了文中所提预处理技术因引入电流磁流间耦合作用而对迭代收敛效果的影响。

考察文中所提预处理技术对于复杂目标的计算效果。目标的几何结构如图3所示。入射角度θ为45°，Φ为90°，带槽长方体的介电常数为4－j，空气中的平均边长为0.3λ0，未知数个数为15 340.采用无预处理求解，BP以及文中所提预处理技术所需要的计算资源见表6所示。对于有耗媒质，收敛速度快于无耗媒质。其余结论与前面算例一致，文中所提预处理方法效果明显，相对于BP有更高的计算效率。

表5 边长为4λ0的介质立方体（ε＝4）无预处理，BP与文中所提预处理技术所需计算资源比较

图3 带槽长方体几何结构示意图

表6 带槽长方体（ε＝4－j）无预处理，BP与文中所提预处理技术所需计算资源比较

为了展示预处理后的CTF对电大尺寸目标的计算能力，计算了直径为10λ0，介电常数为2的电大介质球体散射。在此计算中，剖分尺寸为0.4λ0，未知数个数为42 140.采用无预处理求解、BP以及文中所提预处理方法所需要的计算时间、迭代步数以及内存见表7，数值结果与Mie解析解的比较见图4。从图中可以看出：数值结果与Mie值吻合得很好。应用文中所提预处理技术的效率比不用预处理的效率提高了3倍以上。图5比较3种方法的迭代收敛曲线，文中所提预处理技术具有很好的收敛表现。

表7 直径为4λ0的介质球（ε＝2）无预处理，BP与文中所提预处理技术所需计算资源比较

图5 无预处理，BP与文中所提预处理技术的收敛率比较

3 结 论

针对高阶矩量法求解介质体散射问题时存在的矩阵性态差、迭代求解效率低的缺点，根据CTF方程系数矩阵具有的特点，提出了一种基于ILUT的高效预处理技术，并将其成功地应用于高阶矩量法求解均匀介质体散射问题中。数值实验表明：相比BP，采用文中所提预处理技术，能极大地提高迭代求解的速度。

［1］NOTAROŠB M.Higher order frequency－domain computational electromagnetic［J］.IEEE Trans Antennas Propag，2008，56（8）：2251－2276.

［2］DJORDJEVIC M，NOTAROŠB M.Double higher order method of moments for surface integral equation modeling of metallic and dielectric antennas and scatterers［J］.IEEE Trans Antennas Propag，2004，52（11）：2985－2995.

［3］任 仪，聂在平，赵延文.基于高阶叠层基函数的加速迭代求解方法［J］.电波科学学报，2008，23（1）：100－105.REN Yi，NIE Zaiping，ZHAO Yanwen.An acceleration iterative solution of MoM matrix equation based on higher order hierarchical basis functions［J］.Chinese Journal of Radio Science，2008，23（1）：100－105.（in Chinese）

［4］弓晓东，胡 俊，聂在平，等.三维导电目标电磁散射的高阶多层快速多极子方法［J］.电波科学学报，2004，19（5）：577－580.GONG Xiaodong，HU Jun，NIE Zaiping，et al.Higher order multilevel fast multipole algorithm for solving electromagnetic scattering from 3－D perfectly electric conductor［J］.Chinese Journal of Radio Science，2004，19（5）：577－580.（in Chinese）

［5］SHENG X Q，JIN J M，SONG J，et al.Solution of combined－field integral equation using multilevel fast multipole algorithm for scattering by homogeneous bodies［J］.IEEE Trans Antennas Propag，1998，46（11）：1718－1726.

［6］ERGUL O，GUREL L.Comparison of integral－equation formulations for the fast and accurate solution of scattering problems involving dielectric objects with the multilevel fast multipole algorithm［J］.IEEE Trans Antennas Propag，2009，57（1）：176－187.

［7］MALAST，GÜREL L.Approximate Schur preconditioners for efficient solutions of dielectric problems formulated with surface integral equations［C］//Computational Electromanetics International Workshop，2009：44－49.

［8］LEE J F，ZHAN J Z，LU C C.Incomplete LU preconditioning for large scale dense complex linear systems from electromagnetic wave scattering problems［J］.Journal of Computational Physics，2003，185（1）：158－175.

［9］郭景丽，李建瀛，邹艳林，等.金属目标快速分析的不完全LU预处理技术［J］.电波科学学报，2008，23（1）：141－144.GUO Jingli，LI Jianying，ZOU Yanlin，et al.Incomplete LU pre－conditioner technology for fast analysis of conducting objects［J］.Chinese Journal of Radio Science，2008，23（1）：141－144.（in Chinese）

［10］HU F G，WANG C F，GAN Y B.Efficient calculation of interior scattering from large three－dimensional PEC cavities［J］.IEEE Trans Antennas Propag，2007，55（1）：167－177.

［11］JØRGENSEN E，VOLAKKIS J L，MEINCKE P，et al.Higher order hierarchical Legendre basis functions for electromagnetic modeling［J］.IEEE Trans Antennas Propag，2004，52（11）：2985－2995.

［12］GRAGLIA R D，WILTON D R，PETERSON A F.Higher order interpolatory vector bases for computational electromagnetic［J］.IEEE Trans Antennas Propag，1997，45（3）：329－342.

［13］DJORDJEVIC M，NOTAROŠB M.Higher－order hierarchical basis functions with improved orthogonality properties for method of moments of metallic and dielectric microwave structures［J］.Microw Opt Technol Lett，2003，37（2）：83－88.

［14］SUN D K，LEE J F，CENDES Z.Construction of nearly orthogonal Nedelec bases for rapid convergence with multilevel preconditioned solvers［J］.SIAM J Sci Comput，2001，23（4）：1053－1076.