多输入多输出雷达发射天线低旁瓣设计
2012-09-18马晓峰汤永浩盛卫星
马晓峰 汤永浩 盛卫星
(南京理工大学电子工程与光电技术学院,江苏 南京 210094)
引 言
为有效提高雷达系统的威力和抗干扰能力,要求其天线具有窄波束、高增益、低旁瓣。现有的有源相控阵雷达、数字阵列雷达,通常采用幅度加权的方式来抑制旁瓣电平,该方法的缺点是每个阵元的功率无法充分利用,加窗还会造成波瓣展宽、能量泄露等问题。有文献讨论采用子阵优化布阵的方法来降低旁瓣和抑制栅瓣[1-2],但依然需要采用加窗处理的方法;也有文献讨论相控阵唯相位的发射波束形成方法,但是由于自由度的限制,低旁瓣优化程度有限[3-4],无法满足实际需要。
多输入多输出(MIMO)雷达是近期雷达领域的研究热点。其中,集中式 MIMO雷达[5-6]由于波形多样性带来了额外的自由度,为设计更低旁瓣的发射波束方向图带来了可能。适当地设计阵元间发射波形的相关性,可以使得天线辐射能量集中于空间感兴趣的区域,或者匹配于一个给定的方向图,同时能够确保感兴趣的多目标之间的回波相关性最小,从而有效提高接收端自适应阵列信号处理算法的性能[7-12]。本文针对集中式 MIMO雷达(以下简称MIMO雷达)的低旁瓣发射波束形成的需求展开阵元发射波形的优化设计。
基于MIMO雷达的发射波形设计,发射信号之间的互相关特性都是可以任意选择的。为了能够充分利用波形多样性带来的自由度,文献[7]-[12]都采用通过优化信号之间的相关矩阵R的方法来设计波形,以匹配期望的方向图。这一类设计思想着重于波束形状的匹配,而对旁瓣的约束不是很严格,设计出的方向图旁瓣一般比较高。在实际工程应用中,我们更加倾向于能够获得具有较低旁瓣的方向图设计方法。文献[12]在确定的主瓣指向条件下,约束主瓣宽度,而对旁瓣区域则使得其最大值与主瓣峰值的差值最小,这是一个负值,因此是一个凸优化问题。这种方法优化出来的方向图在满足一定区域的主瓣宽度要求外,也拥有很低的旁瓣电平。然而,这种方向图的旁瓣区域仍有一个“突起”——第一旁瓣电平比其他旁瓣高很多,这就意味着旁瓣仍有可以抑制的空间。为了消去这个“突起”,文献[12]给出的解决办法是在保证发射总功率恒定不变的情况下,允许每个阵元的发射功率有一个20%的上下浮动值,这样能消除“突起”使得方向图具有更低的旁瓣电平。然而,这种方法的实质与幅度加权的方法是类似的。
如果可以优化发射波束的旁瓣区域,使该区域旁瓣电平保持平坦,则可以获得理论最低的最高旁瓣电平。以此为出发点,提出了一种极小极大准则下的旁瓣电平优化算法,能够在保证阵元等功率的情况下很好地解决旁瓣区域电平变化剧烈这一问题,从而获得更低的第一旁瓣电平;接着,为了采用迭代算法优化求解,我们将上述有约束优化问题简化为无约束优化问题,并采用拟牛顿迭代法求解;最后,采用循环(CA)算法获得易于数字阵列系统实现的相位编码信号。
1 模型建立
考虑一个由M个阵元组成的均匀直线阵,阵元发射的信号为窄带信号,阵元间距为半波长。假设第m个阵元在第n个采样快拍发射的基带信号为xm(n),则在空间角度θk处合成的基带信号为
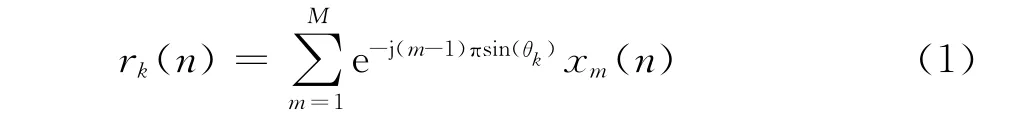
记阵列发射信号向量x(n)=[x1(n),x2(n),…,xM(n)]T,阵列在θk方向的导向性矢量为

则式(1)可以写成向量形式为

式中(·)H为共轭转置。因此,在空间θk处合成的能量大小为
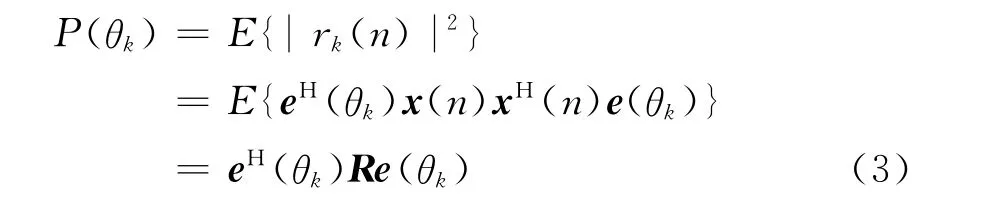
式中:E(·)为期望操作;R为发射信号x(n)的相关矩阵,即

实际应用中,相关矩阵R可以通过N次快拍估计得到,有
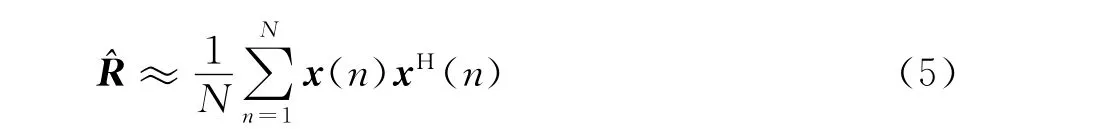
公式(3)给出了发射方向图的表达式,通过对R矩阵的优化,在保证阵元等功率的条件下,可以使得方向图P(θk)具有所期望的低旁瓣特性。
因为R是信号波形的相关矩阵,因此,必然是一个半正定Hermit矩阵。此外,为了充分利用每个阵元的功率,提高雷达作用距离,要求每个阵元的发射功率放大器均工作在饱和状态,也就是矩阵R的对角元素应该都相等[9]。矩阵R的约束条件可以表述为
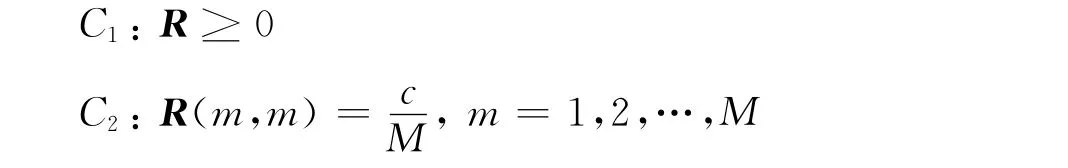
式中c表示发射总功率。
给出R矩阵的优化准则和优化算法,并仅考虑R为实矩阵的情况,此时得到的方向图以法线方向对称。若要获得非对称方向图,可以使用公式(6)对实矩阵R进行处理,得到等效的复相关矩阵。即

式中:φ为方向图平移角度,对于波束形成的应用,该角度即为波束指向角度;~R为复相关矩阵;⊙表示元素的Hadamrd积。
2.相关矩阵优化
针对阵元等功率条件下,低旁瓣发射波束形成的要求,提出一种极小极大旁瓣电平的优化方法,在保证阵元功率充分利用的条件下,使得最大旁瓣电平尽量的小,使所有旁瓣峰值大小大致相同,从而达到低旁瓣的目的。这种有约束优化问题可以描述如下:
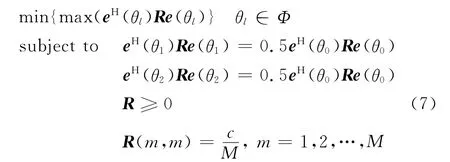
式中:θ0为主瓣指向角度;θ1和θ2分别为左右-3 dB功率点,所以θ2-θ1为主瓣宽度;Ф为旁瓣区域。该问题的约束条件保证了在每个阵元功率充分利用,且在满足一定主瓣宽度的条件下,得到旁瓣电平最小化的优化结果。这个问题可以使用凸优化工具箱(CVX)求解[13]。
上述优化问题是一个约束优化问题,如果能去除式(7)的约束条件,就可以转化为无约束优化问题,从而便于使用多种经典迭代算法求解,提高该问题求解的通用性;另外,无约束优化问题经过进一步推导还可以得到闭式解[9]。基于上述考虑,可借鉴多维球坐标的定义来消去式(7)的约束条件,并修改目标函数将这一问题转化为无约束优化问题[9],然后采用经典的DFP拟牛顿法来解决这一最优化问题。具体的步骤如下:
第一步,相关矩阵R的去约束化。参考文献[9],引入一个R的均方根因子来保证R的半正定性,即

式中,Q是一个上三角矩阵,且满足R一定是半正定的。
为了保证R中对角元素是相等的,要求Q矩阵每一列的范数都相等。采用多维球坐标的方法,定义上三角矩阵Q 如式(9)所示,其中,φ = [φ21,φ31,φ32…,φM,M-1]T.这就将受约束的矩阵R的优化转化为无约束向量φ的优化。因为R为φ的函数,可以将其记为R(φ).
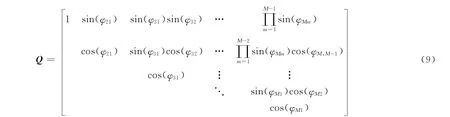
第二步,主瓣宽度的去约束化。由约束条件可以知道,主瓣宽度是由两个-3dB功率点来约束的。可以将这一约束条件加入优化的目标函数,即定义

根据拉格朗日乘数法并考虑该问题对称性质,可对式(7)的目标函数作如下修改
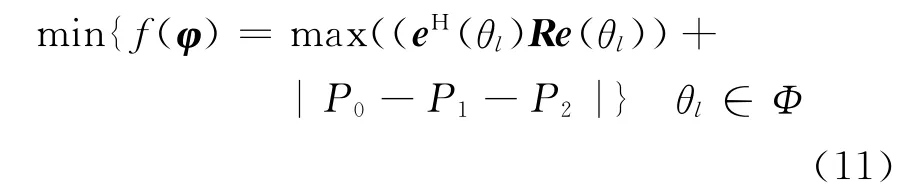
由于发射波束方向图是对称的,故可以保证式(11)取最优值时,P0、P1、P2必然满足如下条件

经过以上两步的变换,可以将式(7)的约束优化问题变为无约束优化问题,从而可以采用简单的无约束优化方法来求解。
需要指出的是,牛顿法虽然是一种经典的无约束优化算法,但是在解决该问题时却无法全局收敛。这是因为:牛顿法的基本思想是将目标函数f(φ)泰勒公式展开,用二次函数近似f(φ),并用迭代点指向近似二次函数的极小点的方向来构造搜索方向,从而具有二阶收敛速度,但是当Hesse矩阵不正定时,并不能保证所产生的方向是目标函数的下降方向,若Hesse矩阵奇异时,会造成算法无法进行下去。此外,牛顿法每一步迭代都需要计算目标函数的二阶导数,即Hesse矩阵,对于大规模问题计算量惊人。然而拟牛顿法可以克服这些缺点[14],因此采用拟牛顿法来计算该最优化问题。
DFP拟牛顿法是第一个拟牛顿校正,它是求解无约束优化问题最有效的算法之一。它的好处是最优步长的选取避免了Hesse矩阵及其逆矩阵的计算。在式(11)最优化问题的每一步迭代过程中,Hesse的奇异性是不可避免的,而采用DFP校正法可以很好地避免这一问题,从而能够用经典的方法来解决这一优化问题,得到近似的结果。
3 相位编码信号优化
在优化得到满足需求的相关矩阵R的基础上,接下来需要解决的是如何从R得到数字阵列雷达能够发射的信号波形X,使得信号波形X的相关矩阵等于或者近似于矩阵R.
若假设发射信号X∈CL×M,其中L为信号波形快拍数或者码元长度。由式(4)可以得到X与其相关矩阵R之间的关系满足

式中U是一个L×M维半正交矩阵(UHU=I)。当然,发射信号X仍然受到恒模条件的约束(记为C)。为了得到满足约束条件C的X,或者至少是一个近似的解,可以将其归为一种数学规划函数问题,即
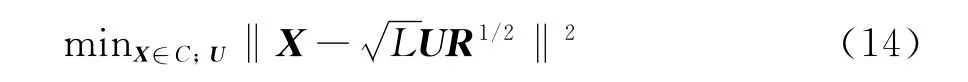
文献[11]提出一种循环(CA)算法,来优化式(14),文献[15]根据二进制相移键控(BPSK)或者四进制相移键控(QPSK)信号的相关矩阵Rg与满足优化准则的R之间的非线性关系,直接用式(13)推导出X与R之间的关系式。
为了说明第二节低旁瓣MIMO雷达的相关矩阵优化在工程上的可实现性,采用文献[11]的CA算法,以第二节得到的相关矩阵R为基础,优化得到具有恒模特性的相位编码发射波形X.CA算法的主要思想是:先确定U(或者X),优化X(或者U)满足式(13),然后在求得的X(或者U)基础上,优化U(或者X),如此反复,直到式(13)小于给定误差为止。具体算法推导可以参考文献[11]、[16]。
4 计算机仿真
在下面所有的仿真例子中,假设MIMO雷达系统发射阵列为均匀线阵,发射阵元数为M,阵元间距为半波长,归一化发射总功率为c=1,并且每个阵元发射功率相等。
4.1 基于相关矩阵R的发射方向图设计
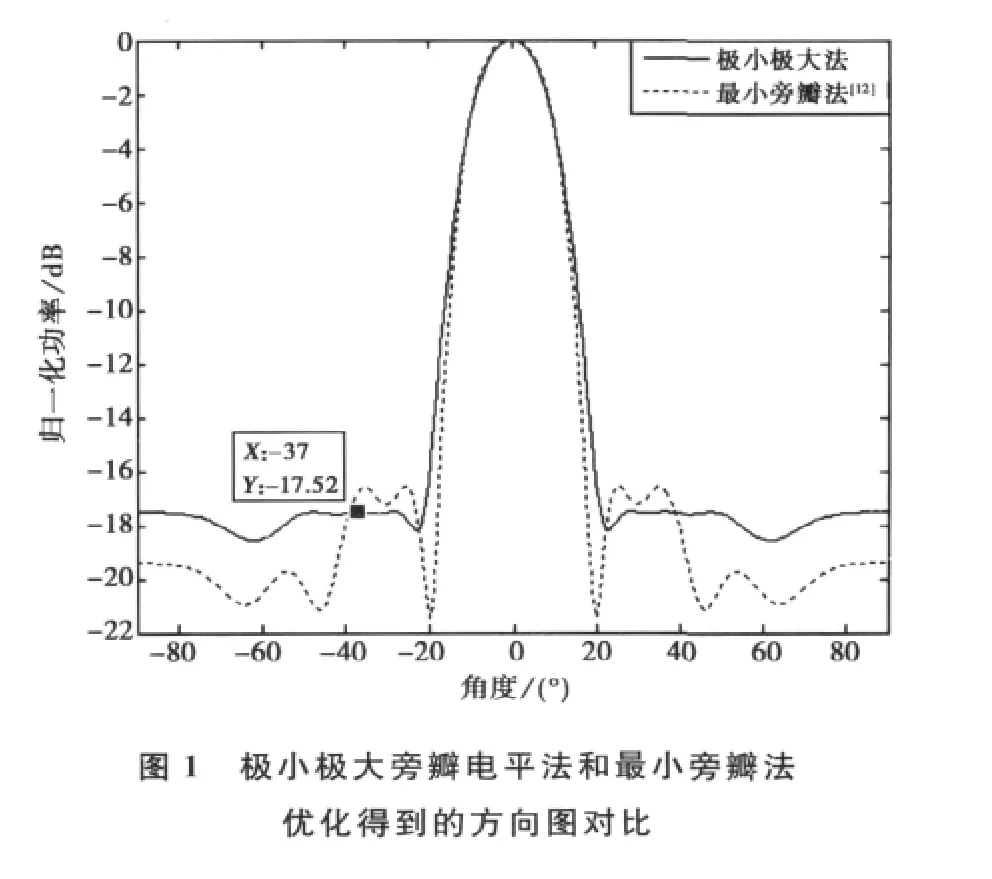
假设主瓣指向0°,主瓣宽度为20°,此时主瓣的两个3dB功率点分别为θ1=-10°,θ2=10°.旁瓣区域为Ф ∈[-90°,-20°]∪[90°,20°].M=10的情况下,图1分别画出了极小极大旁瓣法和文献[12]最小旁瓣法准则下的发射方向图优化结果。可以看到,文献[12]中的旁瓣区域有个“突起”,第一旁瓣峰值电平约为-16.5dB,而在极小极大准则下,通过减少旁瓣区域电平的起伏,可以将第一旁瓣峰值电平拉低至-17.5dB以下。
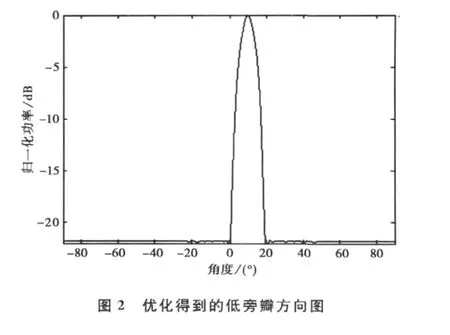
实际工程应用中,方向图主瓣并不总是指向0°,旁瓣电平也需要低于-20dB.针对这一需求,给出下面的仿真设置:阵元M=30,主瓣宽度为8°,主瓣指向10°.采用极大极小准则优化得到指向0°的低旁瓣方向图,再采用式(6)将主瓣平移至10°,优化设计得到的低旁瓣方向图如图2所示,可以看到主旁瓣比优于-22dB,旁瓣区域非常平坦,通过式(6)平移后波束的旁瓣电平提高并不明显。
4.2 相位编码信号设计
本节使用图1极小极大旁瓣电平优化准则得出的相关矩阵R,设计各个阵元的发射相位编码波形,相位编码码长L=64,此时X是一个64×10维的矩阵。
图3为采用CA算法优化得到的10个阵元相位编码信号波形,该波形可以方便地在实际数字阵列系统中实现。

图3 M=10个阵元发射信号的相位编码
图4使用优化得到的发射信号X,计算相关矩阵,并画出方向图。该方向图与理论方向图基本重合,说明CA算法优化得到的发射信号X的相关矩阵很好地逼近期望相关矩阵R.
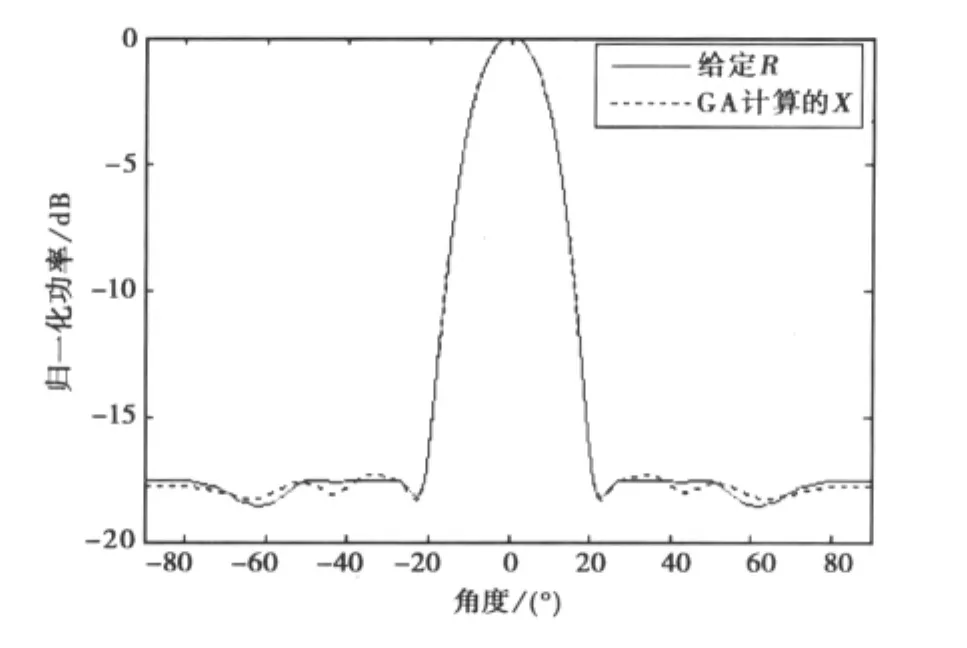
图4 使用优化得到的发射波形所对应的发射方向图与给定相关矩阵R的方向图比较
5 结 论
与传统的相控阵相比,MIMO雷达阵元波形选择具有更大的灵活性,为发射方向图设计提供了更多的自由度。通过优化发射信号的相关矩阵,不需要借助阵元间幅度加权,即可在保证阵元等功率条件下获得满足实际系统要求的低旁瓣高增益发射波束。
本文所提优化方法获得的方向图主瓣宽度,必须适当宽于相同阵元数量的等幅度分布均匀阵的主瓣宽度,如何优化选择集中式MIMO雷达发射波束主瓣宽度,得到更低的副瓣电平,这仍然是一个值得继续研究的课题。
[1]林志强,姚敏立,沈晓卫.基于遗传算法多子阵平板天线旁瓣电平优化[J].电波科学学报,2011,26(2):369-375.LIN Zhiqiang,YAO Minli,SHEN Xiaowei.Sidelobe reduction of the planar antenna with multiple subarrays based on genetic algorithm[J].Chinese Journal of Radio Science,2011,26(2):369-375.(in Chinese)
[2]黄 飞,盛卫星,马晓峰.随机错位子阵阵列天线及其优化设计[J].电波科学学报,2008,23(5):917-921.HUANG Fei,SHENG Weixing,MA Xiaofeng.Plane antenna arrays with randomly staggered subarrays and its optimal design[J].Chinese Journal of Radio Science,2008,23(5):917-921.(in Chinese)
[3]DEFORD J F,GANDHI O P.Phase-only synthesis of minimum peak sidelobe patterns for linear and planar arrays[J].IEEE Trans on Antennas and Propagation,1988,36(2):191-201.
[4]闫秋飞,范国平,徐朝阳.一维唯相位低副瓣技术研究 [J].船舶电子对抗,2009,32(5):52-55.YAN Qiufei,FAN Guoping,XU Chaoyang.Study of low side lobe technique with phase-only on linear arrays[J].Shipboard Electronic Countermeasure,2009,32(5):52-55.(in Chinese)
[5]DAUM F,HUANG J.MIMO radar:snake oil or good idea?[J].IEEE Aerospace and Electronic Systems Magazine,2009,24(5):8-12.
[6]LI J,STOICA P.MIMO radar with co-located antenna:review of some recent work[J].IEEE Signal Processing Magazine,2007,24(5):106-114.
[7]AITTOMAKI T,KOIVUNEN V.Signal covariance matrix optimization for transmit beamforming in MIMO radars[C]∥The Forty-First Asilomar Conference on Signals,Systems and Computers.Pacific Grove,November 4-7,2007:182-186.
[8]FUHRMANN D R,ANTONIO G S.Transmit beamforming for MIMO radar systems using signal crosscorrelation[J].IEEE Trans on Aerosp Electron Syst,2008,44(1):171-186.
[9]AHMED S,THOMPSON J S,MULGREW B,et al.Unconstrained synthesis of covariance matrix for MIMO radar transmit beampattern[J].IEEE Trans on Signal Processing,2011,59(8):3837-3849.
[10]胡亮兵,刘宏伟,刘保昌,等.MIMO雷达发射方向图匹配和波形优化方法[J].西安电子科技大学学报:自然科学版,2009,36(6):1021-1033.HU Liangbing,LIU Hongwei,LIU Baochang,et al.Transmit beampattern matching design and waveform optimization for MIMO radar[J].Journal of Xidian University:Science and Technology,2009,36(6):1021-1033.(in Chinese)
[11]STOICA P,LI J,ZHU X.Waveform synthesis for diversity-based transmit beampattern design[J].IEEE Trans on Signal Processing,2008,56(6):2593-2598.
[12]STOICA P,LI J,XIE Y.On probing signal design for MIMO radar[J].IEEE Trans on Signal Processing,2007,55(8):4151-4161..
[13]GERSHMAN A B,SIDIROPOULOS N D,SHAHBAZPANAHI M B,et al.Convex optimization based beamforming[J].IEEE signal processing magazine,2010,27(3):62-75.
[14]刘韵佛,刘 峥,谢 荣.一种基于拟牛顿法的MIMO雷达发射方向图综合方法[J].电波科学学报,2008,23(6):1188-1193.LIU Yunfo,LIU Zheng,XIE Rong.Transmit pattern synthesis algorithm for MIMO radar based on newton-like method[J].Chinese Journal of Radio Science,2008,23(6):1188-1193.(in Chinese)
[15]AHMED S,THOMPSON J S,MULGREW B,et al.Finite alphabet constant-envelope waveform design for MIMO radar[J].IEEE Trans on Signal Processing,2011,59(11):5326-5337.
[16]TROPP J A,DHILLON I S,HEATH R W,et al.Designing structured tight frames via an alternating projection method[J].IEEE Trans Inf Theory,2005,51(1):188-209.
