继电保护器中的谐波分析*

蒋庆斌 ，钱金法 ，曹德健，赵 力*

(1.常州机电职业技术学院，江苏 常州 213012;2.东南大学信息科学与工程学院，南京 210096)

在实际电网运行中，电力信号不可能是理想的正弦信号，可能含有多次谐波，而谐波的分析关系到继电保护器能否准确动作，比如，电网中的三次和五次谐波会对零序电流、零序电压产生影响，在某些情况下，这种影响可能导致一些保护(包括单相接地选线保护)误动作。此外，谐波分析中，需要对信号进行频谱校正，通过频谱校正算法可以知道实际运行中的信号的基波频率，从而可以用来作为低周减裁保护的判断依据。

我们知道，任何周期信号都可以分解为含有基波频率和一系列为基波频率倍数的谐波的正弦波分量。谐波也是正弦波，且每个谐波也有各自的幅度、频率和相位。采用傅里叶级数对非正弦周期信号进行分析是谐波分析的最基本的方法。在实际运用中，我们处理的一般都是经过模数转换后的信号数据，所以合理的分析方法是使用离散傅里叶变换(DFT)以及快速傅里叶变换(FFT)，目前使用比较多的有三种方法:Rifi 频谱估计法［1］、相位差法频率估计法［2］、FFT+DFT 谱连续细化分析法［3］。其中相位差法频率估计法又有两种不同的方法:通用相位差校正法和分段DFT 相位差校正法。然而对于继电保护器来说，想实现谱细化分析比较困难，一般的继电保护器都是采用一个固定的采样频率，而采用相位差法频率估计的计算量比较可观，所以本文所设计的继电保护器采用Rifi 频谱估计来进行谐波分析。

1 谐波分析的基本原理

“谐波”一词起源于声学［4］，在信号处理方面有着广泛的应用。根据法国数学家傅里叶分析证明，任何周期信号都可以分解为含有基波频率和一系列为基波频率倍数的谐波的正弦波分量。谐波也是正弦波，且每个谐波也有各自的幅度、频率和相位。采用傅里叶级数对非正弦周期信号进行分析是谐波分析的最基本的方法。在实际运用中，我们处理的一般都是经过模数转换后的信号数据，所以合理的分析方法是使用离散傅里叶变换(DFT)以及快速傅里叶变换(FFT)。

在实际的工程应用中，我们不可能对无限长的连续信号进行分析，这肯定不符合工业设计中实时性的要求。我们在对信号采样后，截取一段数字信号来进行分析。在这一过程中，会产生误差或错误。比如波形的离散采样会带来混叠问题，波形截断会产生泄漏问题，不同步采样会带来栅栏效应。

当信号频率不是FFT 的频率分辨率Δf 的整数倍时，由于FFT 的“栅栏”效应引起频谱泄漏，此时信号的实际频率位于FFT 主瓣内两条最大谱线之间，可以借助第二谱线与最大谱线的幅度比值来估计信号的实际频率在两条谱线之间的位置，即基于FFT 幅度比值的频率插值方法，称为Rife 频率估计方法［2］。

在Rife 幅值比值法中，对信号进行截断处理，相当于给信号加一矩形窗。矩形窗由于其旁瓣较高，并有负旁瓣，可能导致变换中带进了高频干扰和泄漏，甚至出现负谱现象［5］，选择一个合适的窗能够有效地抑制谱泄漏提高精度。余弦窗的旁瓣显著减少，能够有效地减少频谱泄漏。故在实际运用中，余弦窗得到了广泛的应用。下面就加窗后的信号进行具体的校正分析。

设信号为单一频率正弦信号

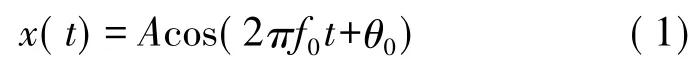
对x(t)进行等间隔Δt=T/N 采样，得到长度为N 的序列

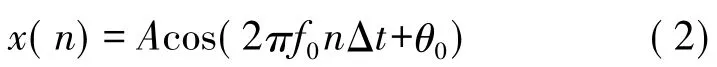
加一个任意窗w(n)后进行离散时间傅里叶变换(DTFT)得到其连续频谱

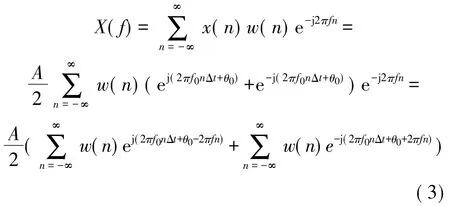
设w(n)的离散时间傅里叶变换(DTFT)为W(f)，做归一化处理后式(3)等价于

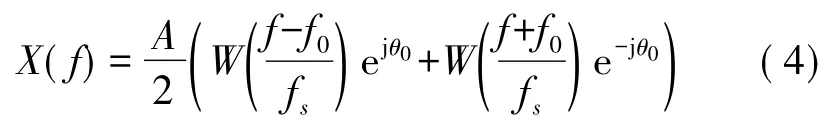
而f=kΔf，k 表示频谱离散后的第几根谱线，代入得到

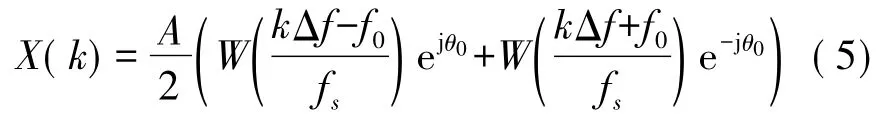
当信号非同步采样时，峰值频率f0=k0Δf 不处于离散谱线上，有窗函数的谱线的对称性可以得到主瓣内谱线幅度最大的两条谱线k1和k2位于k0的邻近，且|k1－k2|=1。则信号DFT 后在k1和k2点对应的幅度分别为

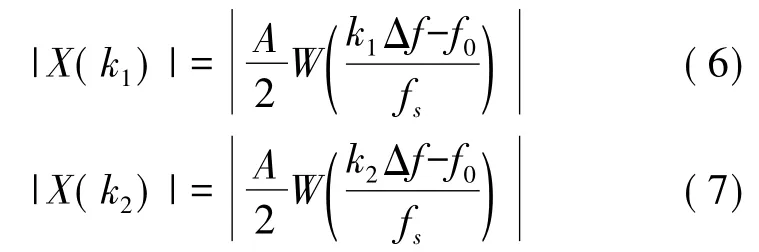
将两式相比可得

上式中只有f0是未知数，可以利用数值方法得到近似解。

2 余弦窗下的幅值比较法

(1)加汉宁窗后的频谱校正分析如上描述，汉宁窗的频域表达式为

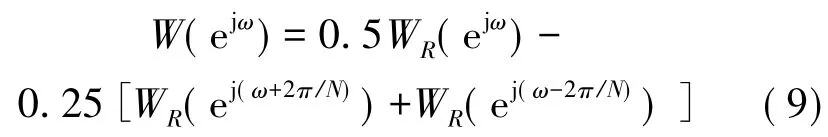
对频域在0～2π 内进行N 的采样，可以得到

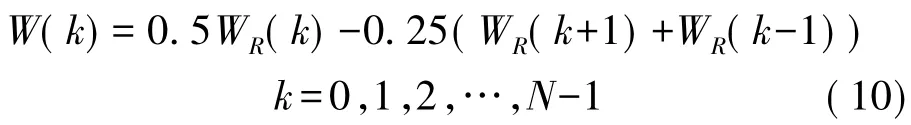
其中WR(k)为

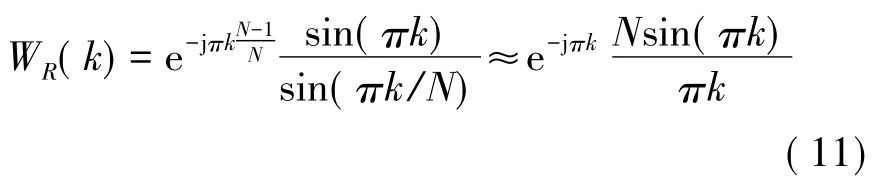
则

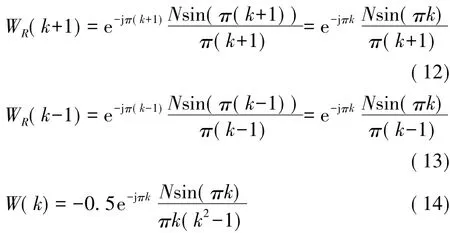
仍然对单一频率信号进行分析，

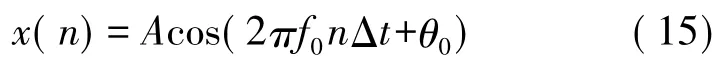
由上一节所分析的加窗后的幅值比较法得到

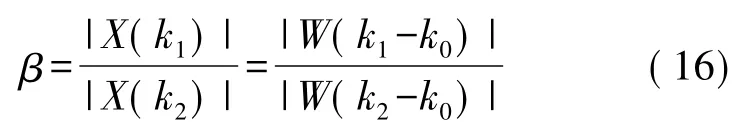
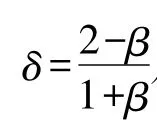
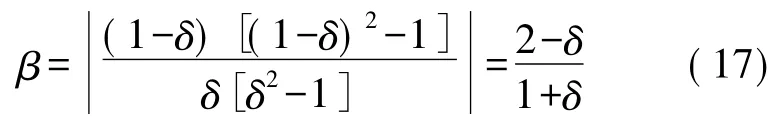
(2)加海明窗后的频谱校正分析海明窗频域采样后的表达式为

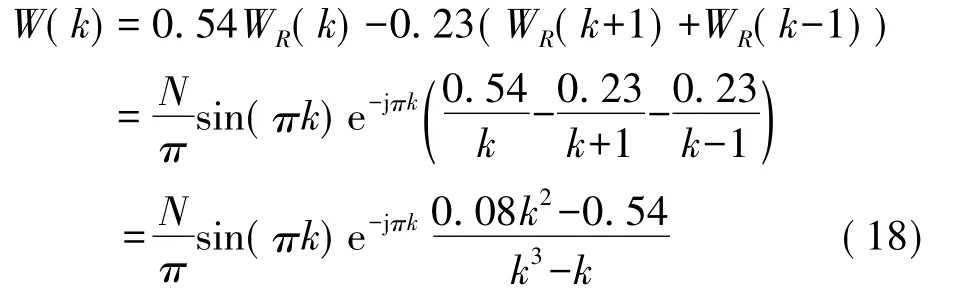
则

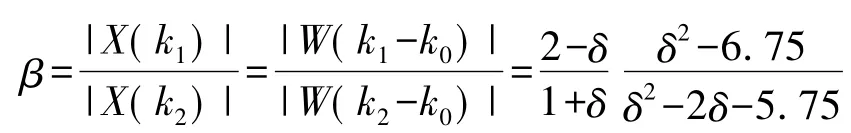
根据数值方法可以得到δ值，即可求得校正后的频谱。

(3)加布莱克曼窗后的频谱校正分析

布莱克曼窗频域采样后表达式为

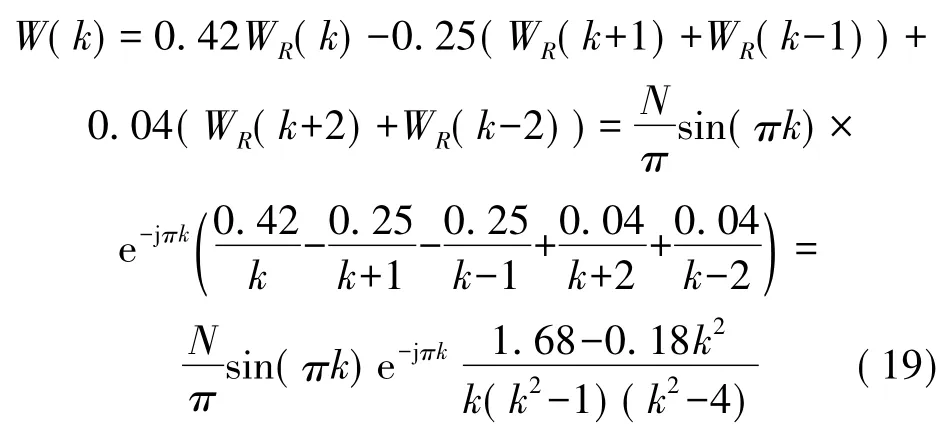
代入式(8)则有

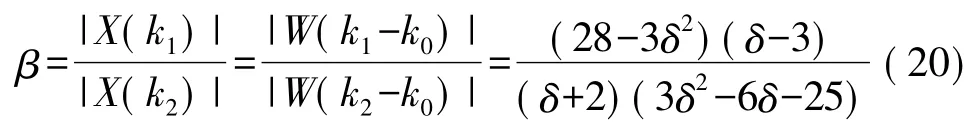
同样可以根据数值方法可以得到δ值，即可以得到校正后的频谱。幅度校正为

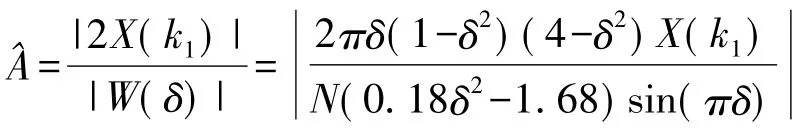
3 幅值比较应用在继电保护器中的改进

由上分析，普通的幅值比较法是通过最大谱线和次大谱线的比值进行校正的，统称为双谱线插值法。通过计算机的模拟，我们发现当信号频率处于最大谱线和次大谱线中心区域是算法精度非常高，均方根误差接近克拉美－罗下限，然而当信号频率位于最大谱线或者次大谱线附近时，算法的精度下降。在电力系统中，信号的基波频率在50 Hz 附近，且我们知道一般情况下信号的最大谱线位于50 Hz，所以为了克服这种误差，根据幅值比较法的思想，选择三条谱线来做幅值比较的分析，称为三谱线插值法。

(1)矩形窗下的校正分析

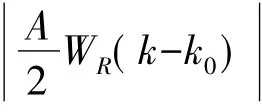
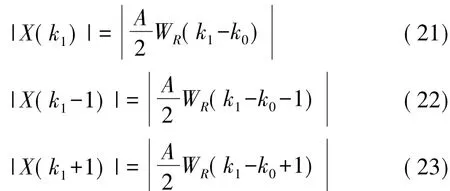
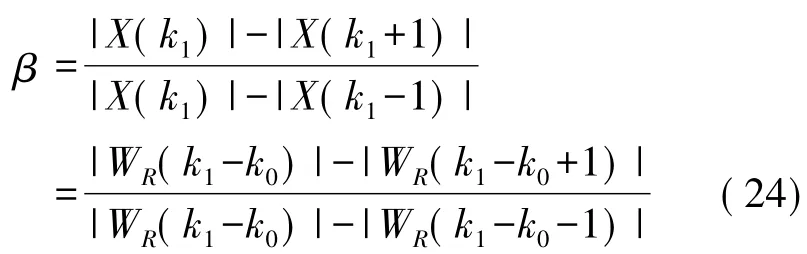
令δ=k1－k0，代入式(24)得

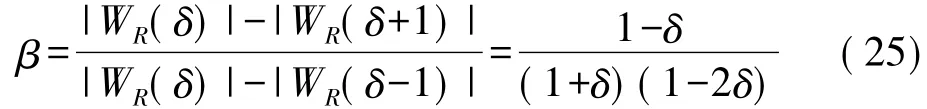
(2)汉宁窗下的校正分析

按照矩形窗下的分析方法，同样应用在汉宁窗下可以得到

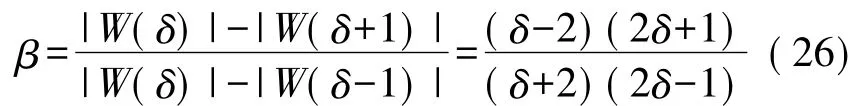
4 仿真分析

在实际电力系统中，电力信号的基波频率f 在45 Hz～55 Hz 之间变动，在本设计中，采样频率fs为1 600 Hz，受限于DSP 芯片的处理速度，通常情况下，取64个点来做FFT。我们知道，电力信号中含有很多谐波分量，所以我们模拟出离散电力信号表达式为

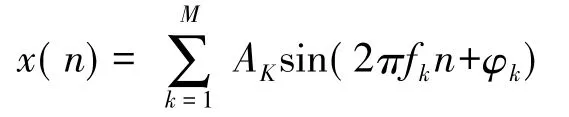
通过实际的测量，模拟了其中的参数，如表1所示。

首先，我们在基波频率处进行了校正，图1中图1(a)表示了不采取任何插值手段时，信号的误差，最大误差达到了6%左右;图1(b)表示了当信号加了矩形窗的Rifi 法插值后的幅度误差，可以看出误差依然很大，最大误差达到3.8%;图1(c)表示了信号加了汉宁窗后的幅值比较法的幅度误差;图1(d)表示了信号采用本文改进的加了汉宁窗后的幅值比较法的幅度误差。

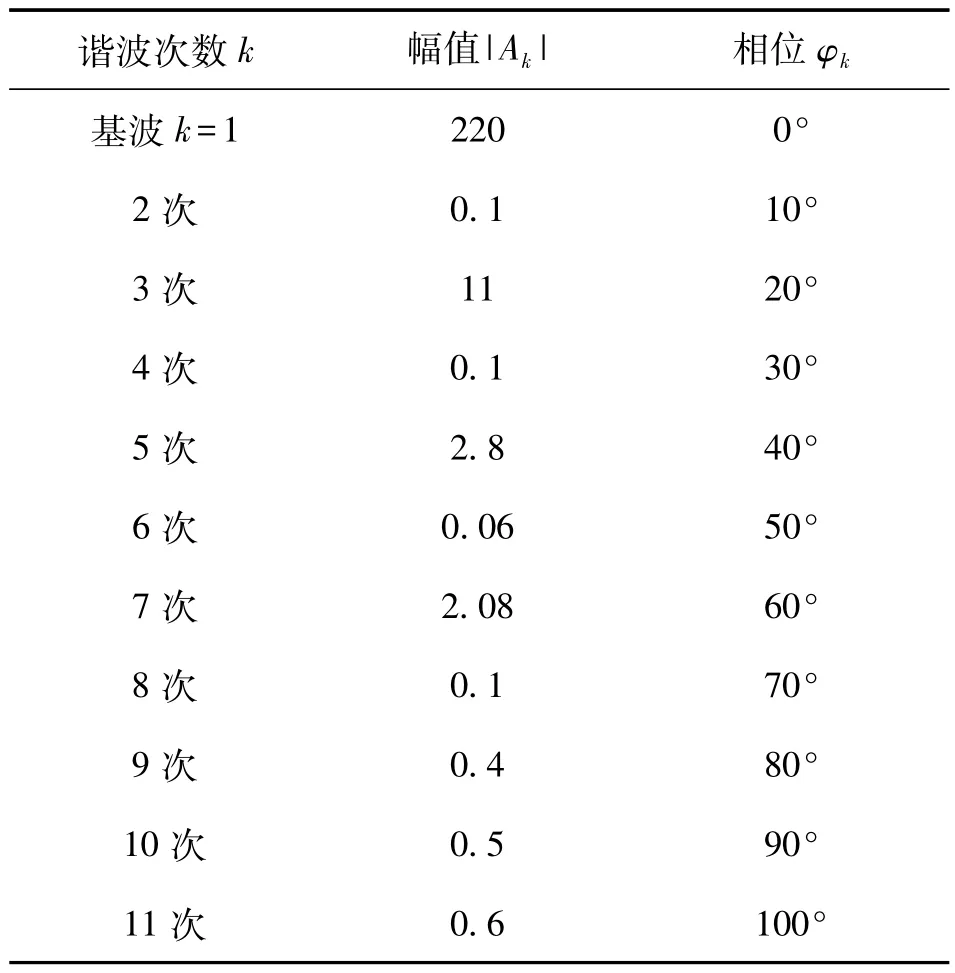
表1 电力信号谐波分量

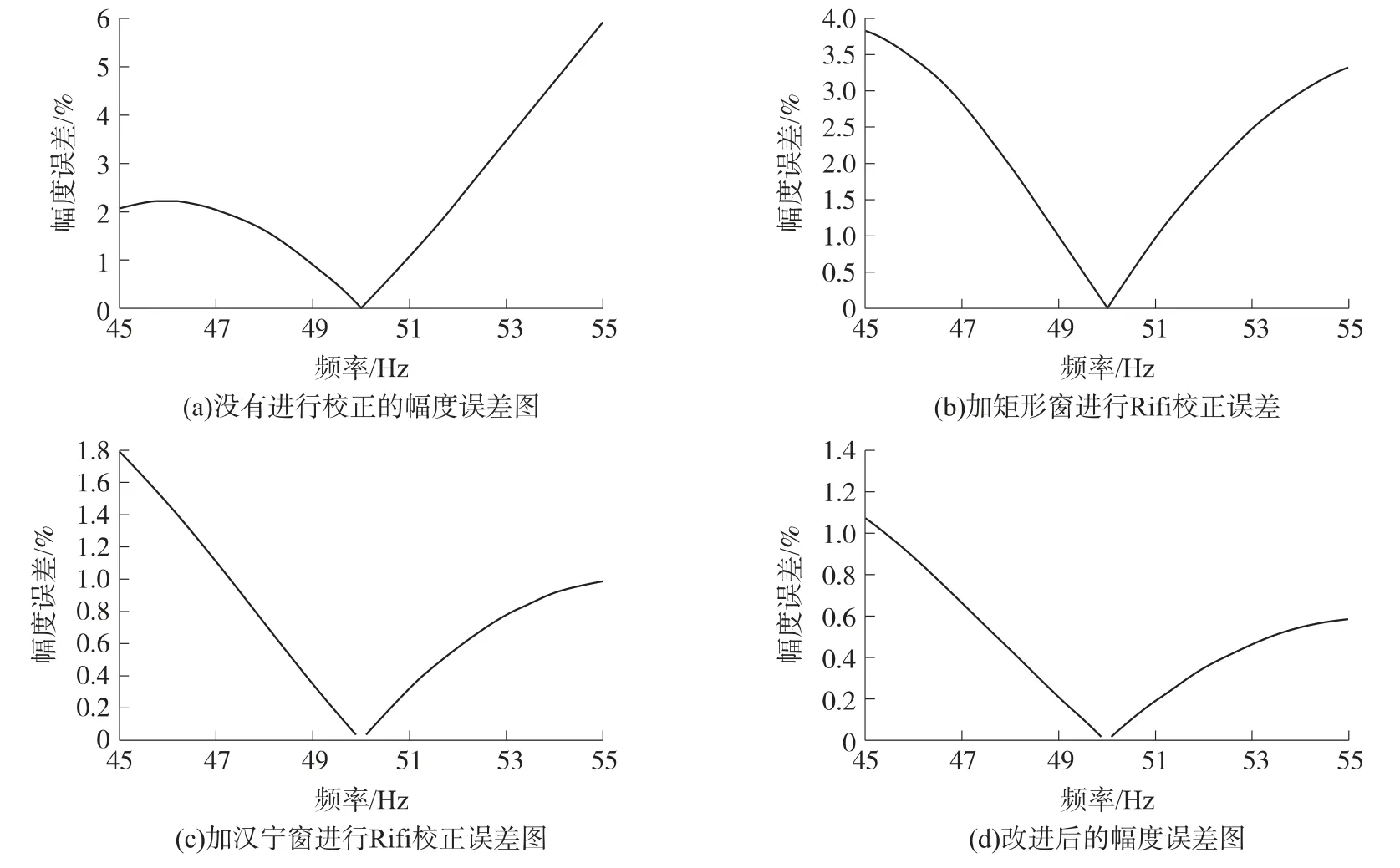
图1 4种校正的幅度误差曲线

5 结论

从图2 中可以看出，本文改进的加汉宁窗的幅度比值法针对电力系统中信号来说，误差最小，达到了继电保护器的谐波参数测量的要求，能够做到比较准确的判断。且我们可以看出三谱线幅值比较法与基本的RIFI 校正计算复杂度差不多。我们在继电保护器中进行测试，发现，三谱线幅值比较法完全满足实时性的要求，是一种能够快速进行谐波分析的方法。

［1］Rife D C，Vincent G A.Use of the Discrete Fourier Transform in the Measurement of Frequencies and Levels of Tones［J］.Bell Sys.Tech，1970(49):197－228.

［2］丁康，钟舜聪.通用的离散频谱相位差校正方法［J］.电子学报，2003，31(1):237－242.

［3］王力，张冰，徐伟.基于MATLAB 复调制ZOOM-FFT 算法的分析和实现［J］.舰船电子工程，2006，26(4):389－392.

［4］王兆安，杨君，刘进军.谐波抑制和无功功率补偿［M］.北京:机械工业出版社，1998:301－400.

［5］Peleg S，Porat B.The CRLB for Signals with Constant Amplitude and Polynomial Phase［J］.IEEE Trans.March 1991，46(3):749－752.

［6］Liguori C，Paolillo A，Pignotti A.Estimation of Signal Parameters in the Frequency Domain in the Presence of Harmonic Interference:A Comparative Analysis［J］.IEEE Transactions on Instrumentation and Measurement，2006，55(2):562－569.

［7］Akke Magnus.Frequency Estimation by Demodulation of Two Complex Signals［J］.IEEE Trans on PWRD，1997，12(1):157－163.

［8］Reljin I，Reljin B，Papic V，et al.New Window Functions Generated by Means of Time Convolution-Spectral Leakage Error［C］//Electrotechnical Conference，Mediterranean，1998:878－881.