基于FPGA 的CRC 编解码器实现*

孙志雄，谢海霞

(琼州学院电子信息工程学院，海南 三亚 572022)

在数字信号传输过程中，由于受到干扰的影响，码元波形将变坏，接收端有可能产生误码。而误码率是衡量数字通信系统的一个重要指标，它关系到通信系统的通信质量。因此，如何降低误码率是通信系统设计所必须考虑的问题。通信过程中产生的误码原因主要是由于传输过程中信道的变化及噪声加入的结果。因此可以在信号传输前进行信道编码，增加信号的冗余度。在接收端进行纠错检错减少噪声的影响，从而尽可能的恢复原始信号，达到减少误码的目的。循环冗余校验码(CRC)就是具有这种强检错功能的技术，由于它的高效率、高性能，实现起来相对简单，因此研究CRC 码的实现具有实际意义［1－6］。

1 CRC 码的原理

在线性分组码中，有一种重要的码称为循环冗余校验(CRC)码。它是在严密的代数学理论的基础上建立起来的。CRC 码除了具有线性分组码的一般性质外，还具有循环性。循环性是指任一码组循环一位(即将最右端的一个码元移至左端，或反之)以后，仍为该码中的一个码组。在下表1 中给出了一种(7，3)循环码的全部码组。

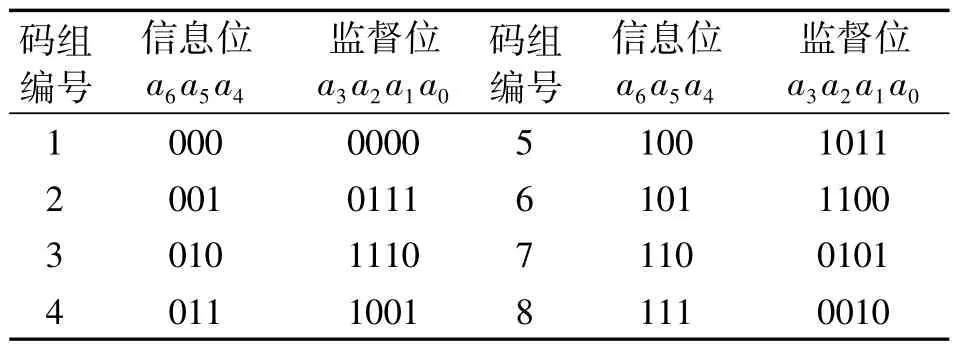
表1 一种(7，3)循环码的全部码组

2 CRC 码的编解码方法

2.1 CRC 码的编码方法

在代数编码理论中，一般把各码组中的码元当作是一个多项式的系数，这种多项式称为码多项式。在CRC 编码时，首先要根据给定的(n，k)值选定生成多项式g(x)，即从(xn+1)的因子中选一个(n－k)次多项式作为g(x)。由于所有码多项式T(x)都可以被g(x)整除。根据这条原则，就可以对给定的信息位进行编码:设m(x)为信息码多项式，其次数小于k。用xn－k乘m(x)，得到的xn－km(x)的次数必定小于n。用g(x)除xn－km(x)，得到余式r(x)，r(x)的次数必定小于g(x)的次数，即小于(n－k)。将此余式r(x)加于信息位之后作为监督位，即将r(x)和xn－km(x)相加，得到的多项式必定是一个码多项式。因为它必定能被g(x)整除，且商的次数不大于(k－1)。因此，CRC 码编码步骤可以归纳为:

(1)用xn－k乘m(x)。这一运算实际上是在信息码后附加上(n－k)个“0”。

(2)用g(x)除xn－km(x)，得到商Q(x)和余式r(x)，即

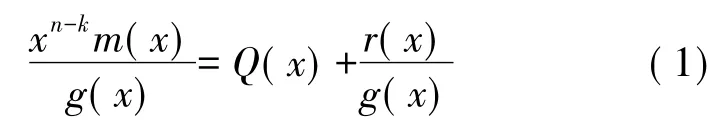
(3)编出的码组T(x)为

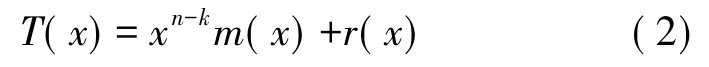
2.2 CRC 码的解码方法

在CRC 编码中，由于任意一个码组多项式T(x)都应该能被生成多项式g(x)整除，所以在接收端可以将接收码组R(x)用原生成多项式g(x)去除。当传输中未发生错误时，接收码组与发送码组相同，即R(x)=T(x)，故接收码组R(x)必定能被g(x)整除;若码组在传输中发生错误，则R(x)≠T(x)，R(x)被g(x)除时可能除不尽而有余项，因此，就以余项是否为零来判别接收码组中有无错码［7］。

3 VHDL 的CRC 编解码仿真及实现

根据CRC 编码方法，利用VHDL 语言编程实现一种(7，3)循环码的编码及仿真，实验采用并行方式输入输出，其生成多项式g(x)为:g(x)=x4+x2+x+1。

对应上述编码方法实现的CRC 编码器的VHDL程序如下:

其CRC 编码仿真波形如图1所示，其中d为信息位，crc为CRC 编码输出，其结果和表1 的CRC编码结果一致。与上述CRC 编码方法相对应的CRC 解码器的VHDL 程序如下:

图1 CRC 编码仿真波形图

其CRC 解码仿真波形如图2所示，其中crc为CRC 解码输入，d为CRC 解码输出，en为解码使能端，高电平有效，其结果和表1 的CRC 编码对应的信息位(即解码)一致。

图2 CRC 解码仿真波形图

在运行上述CRC 编解码器的VHDL 程序并利用Quartus Ⅱ仿真平台进行编译、仿真验证的基础上，将CRC 编解码器的配置程序下载到FPGA 芯片EP1K30QC208－2，并在EDA 实验开发板进行测试，实验结果表明CRC 编解码是正确的［8］。

4 结束语

利用VHDL 语言编程，并基于FPGA 实现了CRC编解码器的设计，体现了软件无线电设计通信系统的思想，是EDA 技术在通信系统设计中的应用，体现了现代电子设计的优越性。VHDL 语言具有良好的可移植性，可以在不同的设计环境和系统平台中使用。另外由于使用FPGA 硬件实现CRC 编解码算法，运行速度比基于CPU 的软件实现速度要快。在此算法的基础上，只要改变生成多项式g(x)，就可以实现其它位数的CRC 编解码器，本文设计思想可以为其它线性分组码的编解码器设计提供借鉴。

［1］刘新宁，王超，胡晨，等.一种快速CRC 算法的硬件实现方法［J］.电子器件，2003，26(1):88－91.

［2］金素梅，王家礼.基于FPGA 的CRC 编码器的实现［J］.现代电子技术，2005(24):18－20.

［3］范绿蓉，栗广云，吴淑君.基于VHDL 语言的CRC 信道编解码电路设计与实现［J］.通信技术，2008，41(6):103－105.

［4］Xu Zhanqi，Yi Kechu，Liu Zengji.A Universal Algorithm for Parallel CRC Computation and Its Implementation［J］.Journal of Electronics(chinese)，2006(4):528－531.

［5］常天海，胡鉴.基于FPGA 的CRC 并行算法研究与实现［J］.微处理机，2010(2):45－48.

［6］郭瑛，俞宗佐.基于FPGA 的循环冗余校验模块设计［J］.内蒙古大学学报(自然科学版)，2010，41(4):417－420.

［7］樊昌信，曹丽娜.通信原理［M］.6 版.北京:国防工业出版社，2006.

［8］江国强.EDA 技术与应用［M］.3 版.北京:电子工业出版社，2010.