具有非线性吸收项的反应扩散方程中的熄灭性质

孙爱慧

（吉林师范大学数学学院，吉林四平 136000）

1 引言及引理

本文研究如下反应扩散方程

其中p≥1，0＜q＜1，λ＞0，β＞0，Ω奂R（NN＞2）是个边界充分光滑的有界区域.

文[1]研究（1.1）-（1.3）解的存在性，熄灭现象是发展方程的一个重要特征，很多学者对解的熄灭性质进行研究；文[2]给出了问题（1.1）-（1.3）中q=1时，λ＞0，β＞0时解的熄灭条件及衰退估计，本文研究0＜q＜1且λ＞0，β＞0时解的熄灭条件，并给出衰退估计.

引理1[3]设y（t）在[0，+∞）上是一个绝对连续的非负正数，且满足

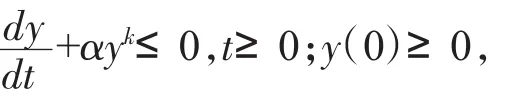
其中 α＞0且为常数，k∈（0，1），则有

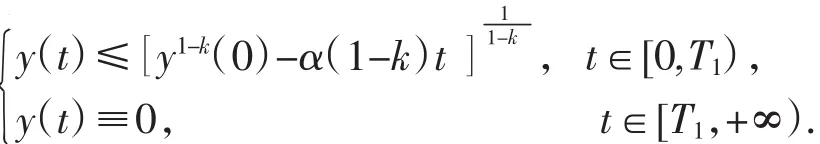
引理2[4]（Gagliado-Nirenbery）设 β≥0，N＞p≥1，β+1≤q且1≤则对于|u|βu∈w1，p（Ω），我们有

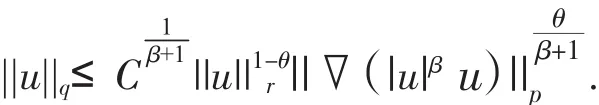
其中θ=（β+1）（r-1-q-1）（N-1-p-1+（β+1）r-1）-1，C~C（N，p，r）.

2 主要结论及证明

定理1假定0≤u0（x）∈L∝（Ω）∩w1,20（Ω）,λ1是方程-Δφ（x）=λφ（x），φ|鄣Ω=0的第一特征值，且 φ1是相应于λ1的特征函数，||φ1||=1，（范数||·||p表示范数||·||Lp（Ω））.

如果 λ＜λ1，则问题（1.1）-（1.3）的广义解在有限时间 T1内熄灭且有

其中 k1，C，T1分别由（2.5）、（2.7）确定.

证明 在（1.1）两端同乘u并在Ω上积分，注意到（1.2），则有

（1）首先考虑p=1情形，即

在（2.3）两端同时取k1次方并利用Young-不等式有

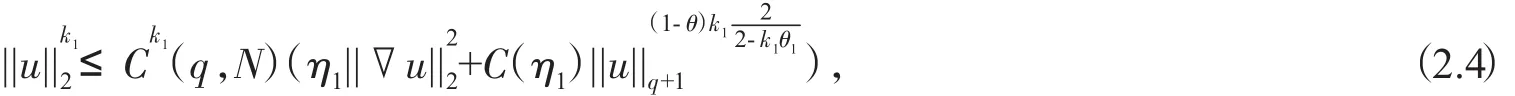
取

显然 k1∈（0，1），则上式化为

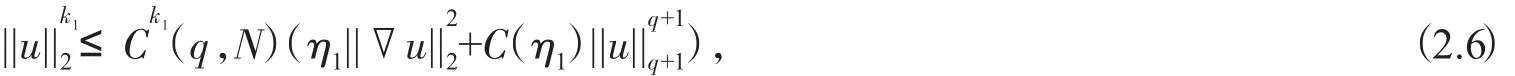
由（2.2），（2.4）以及 λ1为第一特征值有

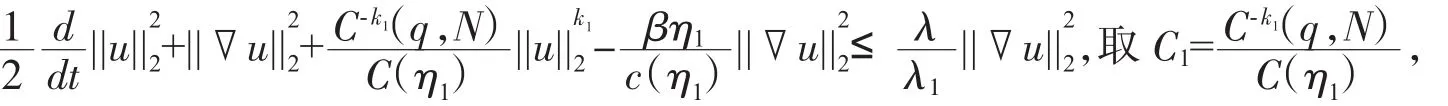
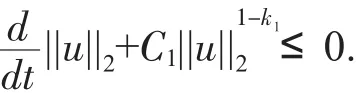
由引理1则有

其中

（2）其次考虑p＞1情形.由于函数 k2φ（x）（其中为问题（1.1）-（1.3）的解，则由（2.1）有

注意到λ1为第一特征值，则有重复q=1情形，可得出定理1结论.

[1]Ladyzenska O.A.,solonikav,V.A.Linear and Quasilinear Equations ofParabolic Type[M].Providence RI:Annear Math Soc,1968.

[2]S.LChen.The extinction behavior ofthe solutions for a class ofreaction-diffusion equations[J].Applied Mathematics and Mechanics,2001,22(11):1352-1356.

[3]W.J.Liu.Extinction properties ofsolutions for a class fast diffusive p-laplacian equation[J].Nonlinear Anal.TMAT,2011(4):4520-4532.

[4]C.S.chen,R.Y.Wang.L∞estimate ofsolution for the evolution.m-lapacian equation with initial value inLq(Ω)[J].Nonlinear Anal.,2002,48(4):607-616.