利用改进相频检测器实现大频偏M-PSK信号的快速载波同步
2012-08-08邱乐德
徐 烽,邱乐德,王 宇
(1.中国空间技术研究院西安分院,西安 710100;2.中国空间技术研究院,北京 100094)
1 引 言
卫星通信信道是典型的非线性信道[1],会引起信号的非线性失真,因此对通信调制方式有一定要求,而M元相移键控(M-ary Phase Shift Keying,MPSK)[2]调制信号具有恒包络特性,非常适合在非线性卫星信道中使用,因此被广泛用于卫星通信,例如QPSK是目前卫星通信最常用的调制方式,而较高速率数据传输的卫星通信中则一般采用8-PSK调制。
卫星通信的数字接收机经常要在较大的频偏下实现载波同步,频偏主要来源于收发端振荡器、混频器、低噪声模块(Low Noise Block,LNB)等的振荡频率不稳定,以及由星-地相对运动引起的Doppler频移。在频偏较大时,使用锁相环(Phase-Lock Loop,PLL)实现载波同步会面临较长的捕获时间,甚至无法实现对频偏的捕获。为此,一般采用辅助捕获的技术扩大PLL的频偏捕获范围。常见的辅助捕获技术[3]包括扫频、环路滤波器切换、辅助鉴频器、相频检测器(Phase and Frequency Detector,PFD)。其中,PFD[4]只对传统鉴相器(Phase Detector,PD)做了少量修改,就大大增加了PLL捕获范围,是较大频偏下实现载波同步的一种好方法,在数字无线通信中被广泛采用。
由于PFD能以很小的代价换取捕获性能的明显提升,在文献[4]之后,陆续有人对基于PFD的载波同步技术进行了研究。文献[5]针对QAM系统,对比分析了使用鉴相器(PD)和相频检测器(PFD)做载波捕获的差别,验证了PFD对载波捕获性能的提高。文献[6]针对高阶QAM信号提出的载波恢复环中,采用了类似PFD的“跟踪保持”算法实现对频偏方向的估计。文献[7]将PFD的“跟踪保持”与精简星座锁相环(RC-PLL)相结合,提高了对高阶QAM信号相偏和频偏的检测能力。文献[8]将PD和PFD结合,实现了对高阶QAM信号的快速捕获和高性能跟踪。Lee等人[9]在将PD和PFD结合的基础上,又增加了一个初始频偏估计模块,使捕获速度最大能提高6倍。Ma等人[10]基于CORDIC算法和PFD设计了一种高阶QAM载波同步环,跟踪环路PDF、PDS和DDS 3种模式运行,达到了快速捕获和减小稳态抖动的效果。
为在较大频偏下实现对M-PSK信号的快速捕获,本文研究基于PFD的PLL的载波同步方法,提出一种PFD的改进方法,可以实现更快速的频率捕获。
2 信号模型
假设理想的符号同步和增益控制,载波跟踪模块要处理的是匹配滤波器输出的符号速率的样值:
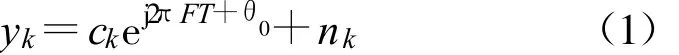
其中,ck是M-PSK复信号,F为频偏,T为符号周期,θ0为初始相偏,nk是复高斯白噪声序列。本文符号ck的调制以8-PSK为例,其调制星座如图1所示。
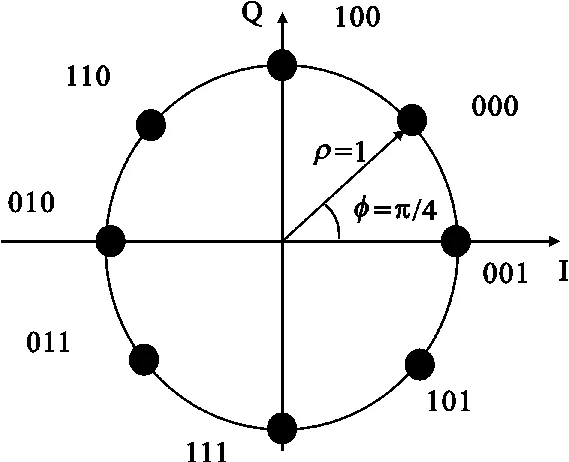
图1 8-PSK星座图Fig.1 8-PSK constellation
3 基本原理
载波同步环基于一般的数字锁相环(Digital PLL,DPLL)实现,如图2所示。主要改动是在PD之后增加一个“跟踪保持”模块,以实现PFD的功能。另外,“锁定检测”模块根据捕获是否成功,调节环路滤波参数,以达到加快捕获或者抑制噪声的效果。
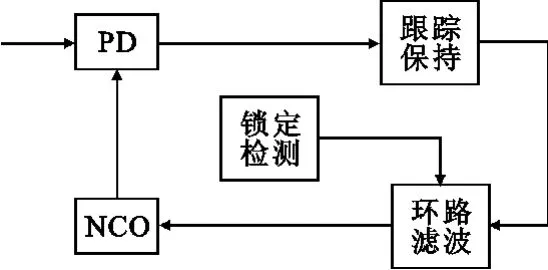
图2 载波同步环结构示意图Fig.2 Carrier recovery loop structure
3.1 PFD的基本原理
Sari和Moridi[4]提出的PDF,在传统 PD的基础上只增加了少量电路,就大大增强了载波跟踪环的频率捕获性能。
如图3所示,细虚线为一个传统正弦鉴相特性的PD鉴相曲线。在稳态时,相位误差在稳定平衡点附近振荡。由于PLL中环路滤波的存在,锁相环的振荡器频率在几个符号之内可以近似认为不变。在捕获过程中,由于存在频偏,相位差会以正比频偏的速率发生变化。假设频偏为F,载波初始相位为θ0,则随时间变化的载波相位为 θ(t)=2πFt+θ0。这样频偏较大时,PD输出的就是一个具有零直流分量的正弦信号,不能提供频偏极性的信息,因此PLL无法控制其VCO的振荡频率捕获频偏;而频偏较小时,使用这样的PD的PLL对频偏的捕获速度也是比较慢的。
为了使PD输出能在有频偏的情况下提供频偏极性的信息,Sari和Moridi[4]在传统PD之后加入一个跟踪保持电路,就构成了PFD。当PD鉴相结果处于稳定平衡点附近的指定范围内时,PFD为跟踪状态,其输出就是PD的鉴相结果;而当PD鉴相结果超出指定范围内时,PFD就变为保持状态,输出值是上一次PFD的输出。例如,在频偏F>0时,鉴相结果会随着时间以图3中向右的趋势变化,从稳定平衡点附近逐渐增大,在超出限定范围后,PFD变为保持状态。由于“保持”段的存在,PFD的输出中就包含了与频偏极性相同的直流分量,因此可以控制VCO提高其振荡频率,从而实现对频偏的捕获。显然,在频偏F<0时,鉴相结果会随着时间以图3中向左的趋势变化,由“跟踪”变为“保持”时,PFD将输出负直流分量,同样能实现对频偏的捕获。
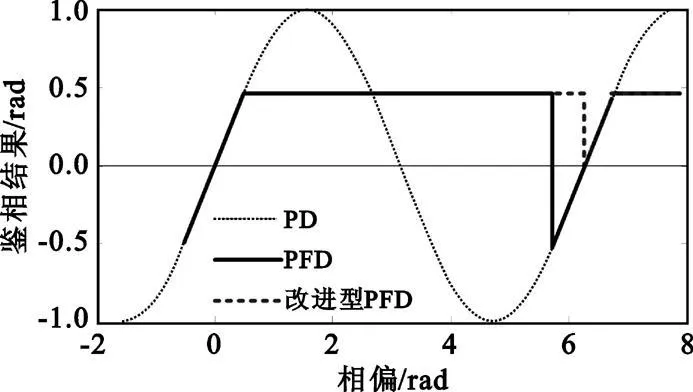
图3 PFD与改进型PFD(正弦鉴相特性)Fig.3 PFD and modified PFD(sine S-curve)
3.2 改进型PFD
从图3(粗实线)可以看出,频偏较大时,上面的PFD在“保持”一段时间后,还会进入到指定的“跟踪”范围,这时PFD输出将跳变为极性相反的输出。而我们知道,这是由于频偏过大导致的,这时正确的输出仍然应该是与频偏极性相同的,或者说,与跳变前“保持”的极性相同的值。因此我们对PFD做如下修改:一是由“跟踪”变为“保持”的条件不变,即鉴相结果超出了“跟踪”范围;二是由“保持”变为“跟踪”的条件,除了要求PD鉴相结果进入“跟踪”区间,还要求鉴相结果的极性与当前“保持”的极性相同。这样改动后,就将上述的相反极性跳变阶段也变成了“保持”段(见图3粗虚线),因此PFD最终输出的直流分量更大,从而可以实现对大频偏更快的捕获。
对M-PSK信号,有不需要定时信息的载波同步方法[11],这里只考虑更常见的符号定时信息已知的情况。M-PSK信号常用的鉴相方法可分为两类[12]:NDA类和DD类。针对上面的载波跟踪结构,我们考察将改进型PFD用于M-PSK信号常见的两种PD:V&V法[13](典型的NDA法)和判决导引(Decision Directed,DD)法[14]。
(1)V&V法
V&V法是一种非数据辅助的(Non-Data Aided,NDA)鉴相方法,其相位误差计算式为
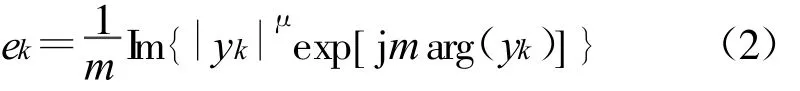
适当选择参数 μ可以起到减小抖动的作用,参数m(等于调制阶数)则是为了消除信号中的调制信息。当 μ=m时,V&V法就变成了幂律法。
V&V的鉴相特性曲线是正弦型的(如图3中的细虚线),由于鉴相结果位于“跟踪”范围内时,除了可能在稳定平衡点附近,也有可能是位于某个不稳定平衡点附近。只有在稳定平衡点附近的“跟踪”范围内时,PFD才应该变为“跟踪”状态;在不稳定平衡点附近的“跟踪”范围内时,PFD应该使用“保持”而不是“跟踪”状态,所以需要一个与正弦PD正交的余弦PD支路辅助判断(详见文献[4]的介绍)。
(2)DD法
在信噪比较高时,由于判决结果可靠度高,采用DD鉴相可以获得更好的性能。DD鉴相的相位误差计算式为

DD法具有锯齿型的鉴相特性曲线(如图4所示),因此可以不需要辅助支路进行“跟踪”区间的判断,而是直接在PD后接入一个跟踪保持电路即可实现PFD的功能。而且,对于具有锯齿鉴相特性的PD,改进型的PFD比一般PFD增加的“保持”区间比例更大,因此,对大频偏捕获性能的提高会更明显。
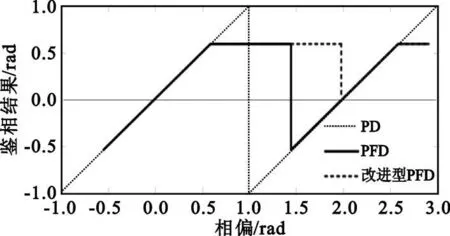
图4 PFD与改进型PFD(锯齿鉴相特性)Fig.4 PFD and modified PFD(sawtooth S-curve)
3.3 锁定检测与参数切换
由于大的鉴相增益和环路带宽有助于快速捕获,而小鉴相增益和环路带宽则有助于抑制噪声、降低PLL相位抖动方差,因此我们设计环路滤波器使用两套参数,在捕获阶段采用大参数,并使用锁定检测模块监视PLL的锁定状态,一旦实现锁定,则切换为小参数,从而实现更好的跟踪性能。
4 捕获性能
下面通过仿真验证对比采用传统PD、PFD和改进型PFD的载波环对频偏的捕获性能。我们使用卫星数传中常见的参数对几种鉴相方法进行仿真,仿真过程使用的具体参数设置如下(这里主要关注捕获,因此使用了较大的环路带宽):调制方式8PSK,帧长度为5 000符号,环路归一化带宽BLT=0.02。
图5给出了不同归一化频偏下DD-PLL对频偏捕获的对比情况。
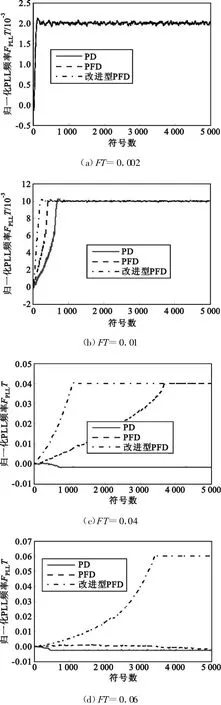
图5 使用PD、PFD、改进型PFD的DD-PLL频响曲线Fig.5 Frequency response of DD-PLL with PD,PFD,and modified PFD
下面对图5进行分析。
(1)在频偏较小(图5(a),归一化频偏 FT=0.002)时,采用PD和PFD、改进型PFD的PLL具有几乎完全相同的频率响应曲线,这是因为较小的频偏使得PD的鉴相结果基本处于“跟踪”区,而“保持”区的设置基本不起作用。
(2)随着频偏的增大,PFD和改进型PFD对频偏捕获的能力逐渐显示出来。在FT=0.01(图5(b))时,使用普通PD的PLL要在超过800符号后才能实现对频偏的捕获,而PFD只需要约500符号就可以实现频偏捕获,改进型PFD比PFD性能更好,约需要300符号就实现了频偏捕获。这说明跟踪保持装置的“保持”功能起到了明显的作用。更多的仿真发现,在FT大于0.005之后,两者对频偏捕获的增强开始显现出来。
(3)当 FT进一步增大到0.04(图5(c))时,使用普通PD的PLL已经无法在仿真长度(5 000个符号)内实现频率捕获;使用PFD的PLL却可在约3 500符号实现捕获;而使用改进型PFD的PLL这时展示出了明显提高的捕获性能,在大约1 200个符号内就实现了捕获。这是因为较大的频偏使得新增的“保持”段出现的概率更大了,因此其提供的直流增益在频率捕获的过程中发挥了更明显的作用。
(4)在 FT增大到0.06(图 5(d))时,使用PD和PFD的PLL都无法在仿真长度内实现频率捕获,而使用改进型PFD的PLL仍然在3 700符号以内实现了捕获,展示出了对大频偏的强大捕获性能。经多次仿真验证,在本文的参数设置情况下,改进型PFD的捕获范围约比传统PFD提升25%。
通过上面的对比,我们可以得出以下基本结论:
(1)在频偏较小时,PD、PFD和改进型PFD的作用基本相同;
(2)在频偏较大时,PFD和改进型PFD才能发挥提高频偏捕获性能的作用;
(3)改进型PFD比PFD具有更大的捕获范围和更快的捕获速度。
另外,在对使用V&V法鉴相的PLL仿真对比后发现(限于篇幅,不再给出仿真结果图),PLL的捕获范围和捕获速度都比DD-PLL低一些,但PFD和改进型PFD同样能提高PLL对较大频偏的捕获性能;在频偏较大时,改进型PFD比PFD的捕获性能也要好一些。
5 结束语
本文对基于PFD的DPLL稍作修改,通过延长PFD的“保持”区间,提高了大频偏下PFD输出的直流分量,从而实现了对更大载波频偏的快速捕获。仿真结果证明,与使用传统PFD的DPLL相比,使用修改后的PFD的DPLL不论是频偏捕获范围还是捕获速度,都有了明显的提高。在归一化频偏大于0.005时,传统PFD与改进的PFD对频偏捕获速度的增强作用开始显现出来,且改进的PFD比PFD的捕获更快;在归一化频偏大于0.06时,在传统PFD无法实现捕获的情况下,改进的PFD仍然能实现对频偏的捕获,验证了改进型PFD对DPLL频偏捕获范围的提高(本文参数设置下提高约25%)。本文使用仿真方法验证了改进型PFD的性能,应用到实际工程中的效果及可能遇到的问题还有待验证。
[1] De Gaudenzi R,Fabregas A G I,Martinez A,et al.High power and spectral efficiency coded digitalmodulation schemes for nonlinear satellite channels[C]//Proceedings of the 7th International ESA Workshop on Digital Signal Processing Techniques for Space Communications.Sesimbra,Portugal:[s.n.],2001.
[2] Proakis J G.DigitalCommunications[M].4th ed.New York:McGraw-Hill,2001.
[3] Gardner F M.Phaselock Techniques[M].3rd ed.New York:John Wiley&Sons,2005.
[4] Sari H,Moridi S.New Phase andFrequency Detectors for Carrier Recovery in PSK and QAM Systems[J].IEEE Transactions on Communications,1988,COM-36(9):1035-1043.
[5] Benani A M,GagnonF.Comparison of carrier recovery techniques in M-QAM digital communication systems[C]//Proceedings of 2000 Canadian Conference on Electrical and Computer Engineering.Halifax,NS:IEEE,2000:73-77.
[6] Ouyang Y,Wang C.A new carrier recovery loop for high-order quadrature amplitude modulation[C]//Proceedings of 2002 Global Telecommunications Conference.Taipei:IEEE,2002:478-482.
[7] Park C,Lee J,Kim Y.Modified Reduced Constellation PLL for Higher Order QAM[C]//Proceedings of 2007 IEEE International Symposium on Circuits and Systems.New Orleans,LA:IEEE,2007:2144-2147.
[8] Gagnon G,Choquette F,Belzile J,et al.A simple and fast carrier recovery algorithm for high-order QAM[J].IEEE Communications Letters,2005,9(10):918-920.
[9] Lee C S,Lee E D,Ahn J.Fast frequency acquisition algorithm for carrier recovery for high-order QAM[J].IEEE Electronics Letters,2008,44(2):143-144.
[10] Ma Siqiang,Chen Yong'en.Implementation and Design of Carrier Recovery Loop for High Order QAM Signals[C]//Proceedings of 20117thInternationalConference onWireless Communications,Networking and Mobile Computing.Wuhan:IEEE,2011:1-4.
[11] Wang Hua,Yan Chaoxing,Wu Nan,et al.Maximum Likelihood Clockless Feedback Phase Recovery for MPSK Signals[C]//Proceedings of 2010 IEEE 72nd Vehicular Technology Conference Fall.Ottawa,ON:IEEE,2010:1-5.
[12] Linn Y.Robust M-PSK phase detectors for carrier synchronization PLLs in coherent receivers:theory and simulations[J].IEEE Transactions on Communications,2009,57(6):1794-1805.
[13] Viterbi A J,ViterbiA M.Nonlinear estimation of PSK-modulated carrier phase with application to burst digital transmission[J].IEEE Transactions on Information Theory,1983,29(4):543-551.
[14] Mengali U,Andrea A N D.Synchronization Techniques for Digital Receivers[M].New York:Plenum Press,1997.
