基于STBC和MRC的多天线分集算法及其性能分析

许 林

(中国西南电子技术研究所,成都 610036)

1 引 言

随着移动用户数目的增加以及人们对通信速率要求的提高,无线通信的容量需求在迅速增长,但现有的无线频谱是有限的,因此如何更高效地利用有限的通信资源成为无线通信新技术发展的焦点所在。多输入多输出(Multiple Input Multiple Output,MIMO)系统通过在发送端和接收端采用多天线技术,大大提高了频谱利用率,同时多天线系统带来的空间分集,可以有效地对抗多径衰落,保证了高速传输的可靠性[1]。V.Tarokh等人在1998年提出了空时分组码(Space Time Block Code,STBC)的概念以及相应的编码规则[2],STBC的提出大大提高了MIMO系统的性能。

但是目前的STBC编码技术中还存在一些亟待解决的问题。首先,空时分组码是针对高信噪比的条件设计的;其次,空时分组码适用于具有丰富多径分量的信道环境;最后,空时分组码的设计主要针对于发送端,而对于接收端言之甚少。相对于STBC而言,最大比合并(Maximum Ratio Combining,MRC)主要考虑如何利用来自多个接收天线的信号来获得最大的分集增益,因此在一定的信道条件下,MRC能弥补STBC的某些不足[3]。

空时码的编码矩阵基于正交设计[4],并采用最大似然译码,以较低的计算复杂度来获得最大的分集增益。最大比合并技术在多径衰落信道中也有着广泛的应用,它通过将不同接收天线收到的信号按权重相加来得到最大的信噪比,从而提高系统的性能。本文在发送端已知信道矩阵 H的情况下,将STBC和MRC技术进行了合并。通过 H动态地对STBC和MRC技术进行选择,使得到的混合系统的信噪比最高,从而提高系统的性能。该算法的性能要优于单独使用STBC或者MRC,可以有效地对抗多径衰落。

2 MIMO多天线技术

2.1 空时分组码技术

空时码是一种用于多发射天线的编码技术,在MIMO系统中有着广泛的应用。空时分组码通过在多根发射天线和各时间周期的发射信号之间产生空域和时域相关性,可以有效地对抗多径信道衰落,提高系统的误码率性能和传输效率。

对于空时分组码(STBC),核心的评价标准是提供发射分集、编码码元发射率以及发射时隙的多少。发射天线的分集度取决于空时编码矩阵的设计方案,如要完全分集,则至少应保证编码矩阵是满秩的。如果配置了多根接收天线,则总的分集度是发射天线数量与接收天线数量的乘积。码元发射率是每单位码元周期内的发射码元的个数。发射时隙是空时编码的长度也就是指码元周期。设计空时编码的最一般的目的是在保持全分集发射的情况下,使码元发射率(速率)最大并且使发射时隙最小。当发射天线数为2时,Alamouti方案可以保证STBC码频带利用率为1,但当发射天线大于2时,通过对编码矩阵的正交设计,STBC码的频带利用率不超过3/4[5]。

当发送天线数为nT、传输一组符号的时间周期数为 p时,STBC码的传输矩阵 X大小为nT×p,STBC码的编码结构如图1所示。

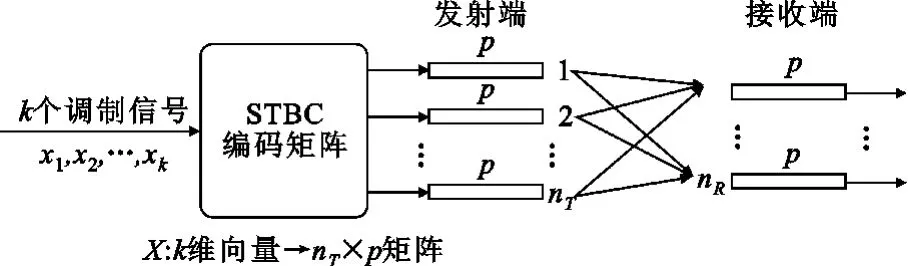
图1 空时分组码系统结构框图Fig.1 Block diagram of STBC

假设每个符号由m个比特组成,每次编码时,km个信息比特映射到信号星座,得到 k个调制信号x1,x2,…,xk,空时分组编码器根据传输矩阵 X生成nT个长度为p的并行信号序列,并通过nT根发射天线发射出去。

由于STBC码采用正交设计,通常采用最大似然(ML)算法来进行译码。当接收天线数为 nR时,接收端收到的信号为

其中,信道H 是nR×nT矩阵,发射端发射信号 sSTBC是nT×p的矩阵,而接收信号 rSTBC和噪声 n是nR×p矩阵,n～N(0,)。因此最大似然译码器为

其中,C为信号调制符号x1,x2,…,xk的所有可能集合,从 C选取与接收信号距离最小的信号序列便得到了STBC译码结果。记ESTBC为发射符号的平均能量,每根天线接收到的白噪声方差为,考虑第m根接收天线(m=1～nR)的第一个时间点收到的信号,信号部分能量是,噪声部分能量是,然后对于nR根接收天线考虑平均效果,总信号能量是,总噪声能量是,可以推出每个时隙中每根天线收到的每个符号的平均信噪比为

2.2 最大比合并技术

最大比合并(MRC)是一种被广泛应用的分集技术,它将各个输入信号按照权重相加得到输出信号,通过对加权因子的选择使输出的信噪比最大。

最大比合并的原理框图如图2所示。

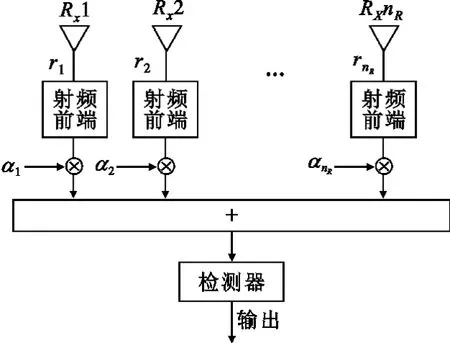
图2 最大比合并原理框图Fig.2 Block diagram of maximum ratio combination

输出信号为所有接收信号的加权线性组合,假设系统的发射天线每个时隙发送同一个符号,经分集合并后输出信号为

3 STBC和MRC相结合的新型多天线系统

STBC和MRC技术均为MIMO系统中常用的分集技术,关于它们的研究已经比较成熟,但根据对信道的动态分析,来选择两者中性能较好的方法进行传输的混合算法还未见到。本文根据对信道的动态分析,提出一种STBC和MRC技术相结合的新型多天线系统。

新系统通过比较两种算法接收端每根天线收到的每个符号的平均信噪比的大小,即 SNRSTBC和SNRMRC的大小来判断采用哪种算法进行传输。当SNRSTBC>SNRMRC时采用 STBC技术,否则采用MRC。根据公式(3)和公式(5),可以得到当

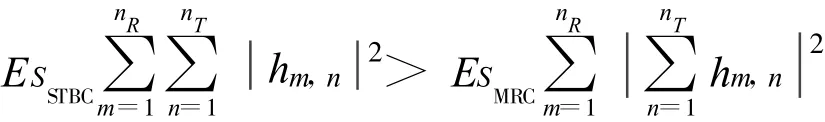
时采用STBC,否则采用MRC。由于STBC码的码率R可能小于1,在比较其信噪比时,把单位比特的能量归一化为1,得到ESSTBC/ESMRC=1/R。对系统的信道矩阵 H,其大小为nR×nT,可以根据SNRSTBC和SNRMRC的大小关系分为两个集合:

当 H∈C1时,采用STBC;当 H∈C2时,采用MRC。

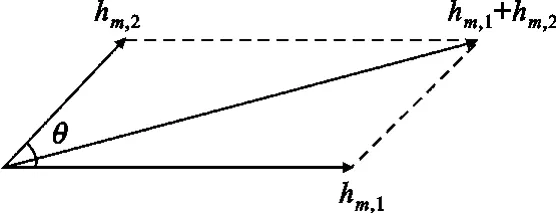
图3 STBC和MRC算法简化比较示意图Fig.3 Simple comparison between STBC algorithm and MRC algorithm

上面考虑的是最简化的例子。当码率R不为1或者天线数比较多时,很难给出闭式解,不过从定性角度考虑,信道的相关性越强则MRC算法更优,否则STBC更优。

MIMO系统的性能通常由成对差错概率(Pairwise Error Possibility,PEP)来表示。记系统的符号错误概率为Pe,f(H)为H的概率密度函数,f(H)=,可以得到

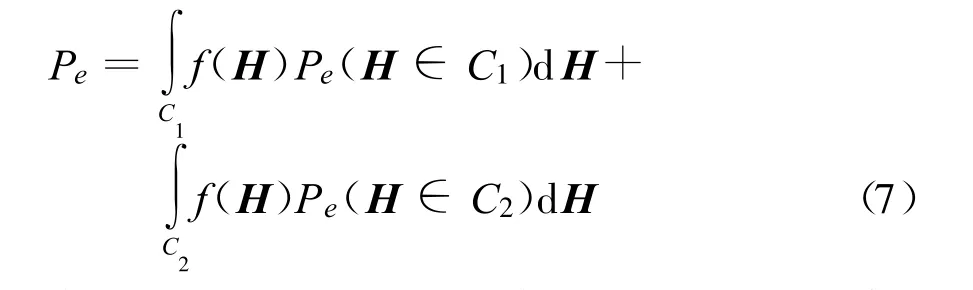
令ΔsSTBC为STBC星座图中两点间的最近距离,其PEP为

对于MRC,令ΔsMRC为其C星座图中两点间的最近距离,由发送和接收方式可以得到

其中:

将公式(8)～(9)代入式(7)可得

4 数据仿真和分析

根据上述分析,本文对STBC、MRC和混合多天线系统分别进行了性能仿真。仿真中采用的MIMO系统发射天线数为4,接收天线数分别为2、3、4。选取的STBC码的码率为1/2,在8个符号周期内通过4根发射天线进行传输,其传输矩阵为

MRC的码率为1,每个符号周期发送同一个符号在接收端进行合并。由于混合系统结合了STBC与MRC,因此其码率不确定。为了保证混合系统的比特传输速率一定,STBC和MRC采用了不同的调制方式,其中STBC采用16QAM调制,8个符号周期发送4个符号共16 bit,此时比特传输速率为2 bit/(s·Hz)。MRC采用4QAM 调制,8个符号周期发送 8个符号共16 bit,比特传输速率也为2 bit/(s·Hz)。因此对混合系统,其比特传输速率也恒定为2 bit/(s·Hz)。在仿真中假设每个星座均采用格雷映射,且比特能量都归一化为1。

接收天线为2、3和4时混合系统的误比特率性能分别如图4、图5和图6所示。图4中,当BER为10-3时,STBC的性能比MRC好了1.5 dB左右,混合算法性能比STBC好3 dB左右。图5中,当BER为10-3时,MRC的性能比STBC好了1 dB左右,混合算法性能比MRC好3 dB左右。图6中,当BER为10-3时,MRC的性能比STBC好了3 dB左右,混合算法性能比MRC好1.5 dB左右。通过对以上结果的比较可以看出,随着接收天线数量的增加,MRC性能的提升快于STBC性能的提升,且混合算法的性能总是优于两种单独的算法。

图4 4×2天线系统中MRC、STBC和混合系统性能对比Fig.4 BER performance of MRC,STBC and their mixed algorithm in 4×2 antenna system

图5 4×3天线系统中MRC、STBC和混合系统性能对比Fig.5 BER performance of MRC,STBC and their mixed algorithm in 4×3 antenna system

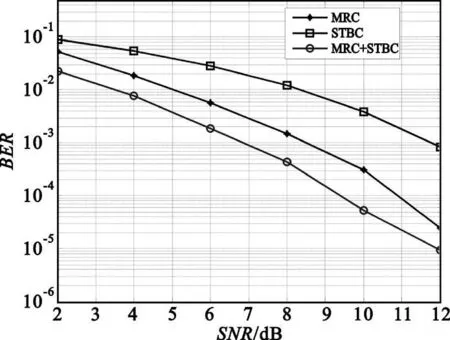
图6 4×4天线系统中MRC、STBC和混合系统性能对比Fig.6 BER performance of MRC,STBC and their mixed algorithm in 4×4 antenna system

5 结 论

STBC和MRC是MIMO系统中常用的两种分集技术,本文通过对这两种技术的分析,在接收端已知信道矩阵H的前提下,提出了一种STBC和MRC混合多天线系统。在瑞利信道下对STBC、MRC及其混合系统的性能进行了理论分析和数据仿真,结果表明,当发射接收天线数目一样时,在相同的发射功率下,混合系统的性能比STBC和MRC均有一定的提升。本文的研究基于信道矩阵已知的条件,现实应用环境中,该条件将会存在偏差,在后续研究中,可以进一步挖掘如何得到准确的信道矩阵信息,以及如何实时反馈动态信息。

[1] Foschini G J.Layered space-time architecture for wireless communication in a fading environment when using multi-element antennas[J].Bell Labs Technical Journal,1996,1(2):41-59.

[2] Tarokh V,Jafarkhani H,Calderbank A R.Space-time block coding for wireless communications:performance results[J].IEEE Journal onSelectedAreas in Communications,1999,17(3):451-460.

[3] RopokisG A,RontogiannisA A,Mathiopoulos P T,et al.An Exact Performance Analysis of MRC/OSTBC over Generalized Fading Channels[J].IEEE Transactions on Communications,2010,58(9):2486-2492.

[4] Tarokh V,Seshadri N,Calderbank A R.Space-Time Codes for High Data Rate Wireless Communication:Performance Criterion and Code Construction[J].IEEE Transactions on Information Theory,1998,44(2):744-765.

[5] Wang Haiquan,Xia Xianggen.Upper bounds of rates of space-time block codes[J].IEEE Transactions on Information Theory,2003,49(10):2788-2796.

[6] Maaref A,Aissa S.Closed-Form Expressions for the Outage and Ergodic Shannon Capacity of MIMO MRC Systems[J].IEEE Transactions on Communications,2005,53(7):1092-1095.