改进的粒子群算法在烧结配料中的应用*
2012-08-08王红君岳有军
赵 辉 ,王 明 ,王红君 ,岳有军
(1.天津理工大学 天津市复杂系统控制理论及应用重点实验室,天津300384;2.天津农学院,天津300384)
在市场经济的推动下,现代钢铁生产成本和经济效益的矛盾十分突出,对于各大钢铁企业来说,降低成本、提高产品质量已迫在眉睫。因此,单一矿种的烧结已经难以满足企业的要求,当今大部分企业已经采用几种矿粉合理搭配进行烧结,这样既可以降低烧结成本,又能提高烧结矿质量。尤其最近各大企业相继增加进口粉和外来铁矿粉的用量,并且随着进口粉和外来粉种类增多,探讨各种原料的合理配比已势在必行[1]。
1 粒子群算法基本原理

粒子群算法采用下列公式对粒子所在位置不断更新:
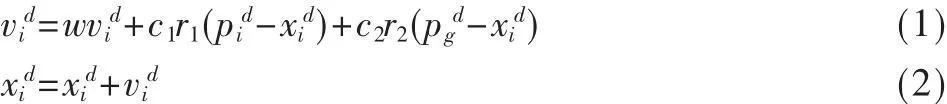
其中,i=1,2,…,m;d=1,2,…,D;w 是非负数,称为惯性权重。加速常数c1、c2是非负常数,通常定义c1=c2=2。r1、r2是在[0,1]区间内均匀分布的随机数。
粒子群算法流程图如图1所示。

算法描述如下:
(1)初始化粒子群。确定种群大小、空间维数、各粒子的随机位置和速度及最大迭代次数。
(2)评价各计算粒子的适应值。
(3)对每个粒子xi,将其适应值与其经历过的最好位置pi的适应值作比较,如果较好,则将xi作为当前的最好位置 pi。
(4)对每个粒子xi,将其适应值与所有粒子经历过的最好位置pg的适应值作比较,如果较好,则将其作为当前所有粒子的最好位置pg。
从收回的有效问卷中,我们针对数据进行统计和整理。数据显示,这次参加问卷调查的计算机类、电气类等理工科学生约占98%,而文史类大学生参加比例仅占2%左右。而对于其他问题,我们从答案中提取了相关数据并对其进行分析和总结。
(5)每次迭代中,根据式(1)、式(2)对每个粒子的位置和速度进行更新。
(6)满足最大迭代次数或全局最优位置满足预定精度要求则停止迭代,输出全局最优解,算法终止,否则跳转步骤(2)继续执行。
2 粒子群算法改进
研究发现在算法的迭代过程中动态地调整惯性权重,可以改变搜索能力的强弱。惯性权重类似模拟退火中的温度,较大的惯性权重有较好的全局收敛能力,而较小的惯性权重则有较强的局部收敛能力。因此,随着迭代次数的增加,惯性权重应不断减少,从而使得粒子群算法在初期具有较强的全局收敛能力,而晚期具有较强的局部收敛能力。例如在参考文献[5]中提出了线性递减权重策略,惯性权重w满足:
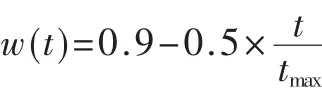
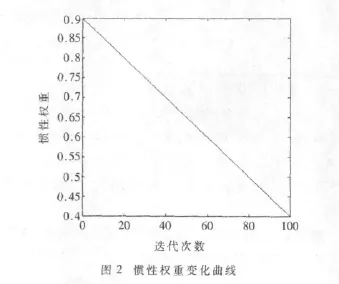
其中,tmax为最大截止代数,将惯性权重看作迭代次数的函数,可从0.9到0.4线性减少。当tmax=100时,惯性权重随迭代次数t的变化曲线如图2所示。
由PSO粒子的搜索特征不难发现,线性减小使其保持较大值和较小值的时间都很短,不能满足搜索初期速度较快、搜索后期速度较慢的要求。为此提出了一种由柯西分布函数演化而来的调整函数,基于此调整函数,开始搜索时能较长时间保持较大值以提高搜索效率,在搜索后期又能较长时间保持较小值以提高搜索精度[6-8]。
柯西分布的累积分布函数:
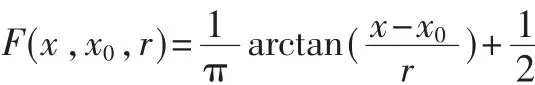
其中,x0是定义柯西分布概率密度函数峰值位置的位置参数,r是最大值一半处的一半宽度的尺度参数。
惯性权重w的改进公式为:
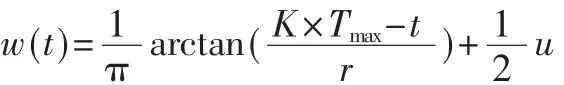
其中,Tmax表示算法的最大迭代数;K∈(0,1),K的大小决定拐点的位置,调整K的值得到不同下降趋势的曲线;t表示当前的迭代数,u为幅度调节参数。柯西分布惯性权重变化曲线如图3所示。
3 烧结矿配料数学模型
3.1 目标函数
由于配料的目的是通过配料比的恰当选择来提高产量、改善质量、降低成本。因此,在建立数学模型的过程中,考虑目标函数时以成本最小为原则[9],建立式(3)所示烧结矿配料目标函数。

式中,i表示参与配比的铁精矿及粉矿的种类数;ci表示各种铁精矿及粉矿的单价(元/t);xi表示各种铁精矿及粉矿的用量(万/t)。式(3)的计算结果与很多因素有关,并受到多种因素的约束。

3.2 约束条件
约束条件主要有烧结矿化学成分约束,如全铁(TFe)、二氧化硅(SiO2)、氧化钙(CaO)、三氧化二铝(A12O3)、氧 化 镁(MgO)、硫(S)、碱 度 控 制(CaO/SiO2)、烧损等[10-11]。考虑烧结矿的化学成分实际上存在波动,因此,用上、下限来进行化学成分的约束,即式(4)和式(5)。

式中,mi和ni分别是烧结矿各种化学成分的上、下限,各种矿石化学成分及约束范围如表1和表2所示。
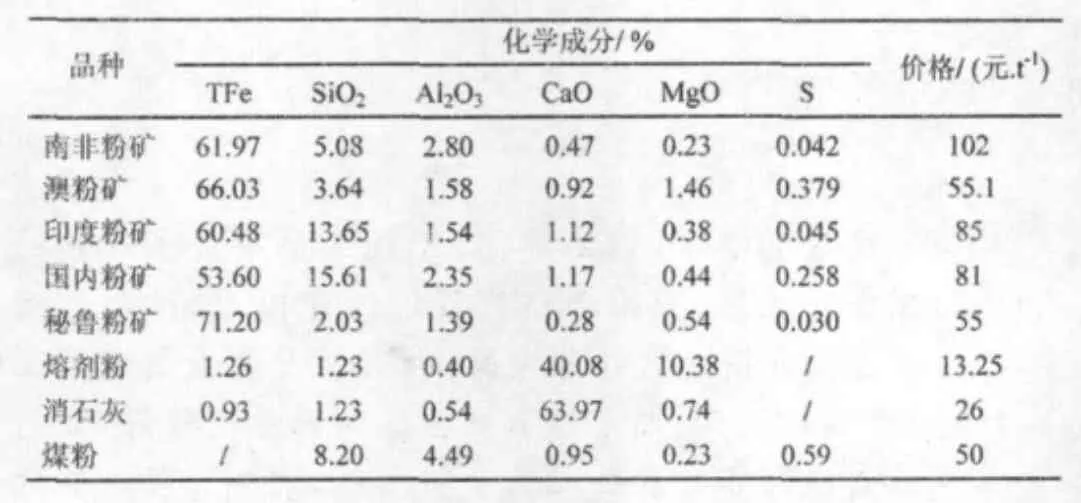
表1 各种铁矿石化学成分及价格

表2 各种铁矿石化学成分约束范围
参与烧结矿配比的各种精铁矿和粉矿有一定的限制:南非粉矿 150~200 kg/t; 印度粉矿 90~200 kg/t; 国内粉矿≤160 kg/t;秘鲁粉矿≥20 kg/t;澳粉矿 300~400 kg/t;消石灰≤50 kg/t;煤粉≤100 kg/t;熔剂粉 200~300 kg/t。 设试验烧结矿成品总量1 000 kg。
4 仿真计算
根据以上数学模型,采用Matlab语言、粒子群算法和改进的粒子群算法,分别编制烧结矿优化配料计算程序,计算出的精铁矿和粉矿需求量及成本如表3所示。其中方案1、方案2、方案3分别代表标准粒子群算法、线性递减惯性权重改进粒子群算法、本文改进粒子群算法的仿真结果。
运用改进粒子群算法对钢铁烧结矿配料进行优化计算,计算机仿真结果表明符合实际工艺要求,通过与标准粒子群算法和线性递减改进粒子群算法的结果相比较,可看出本文提出的改进粒子群算法具有更好的寻优能力和更高的运算精度。由于粒子群算法在优化实现的过程中,不需要对优化问题的数学模型有过高的要求,避免了常规数学方法在求解过程中的复杂性,因此使用人员不需要具备过高、过深的数学理论知识,很适合工程技术人员使用。

表3 各种铁矿石用量及价格仿真结果
[1]梁中渝.炼铁学[M].北京:冶金工业出版社,2009.
[2]EBERHART R C,KENNEDY J.A new optimizer using particles swarm theory[C].Proc Sixth International Symposium on Micro Machine and Human Science,1995:87-92.
[3]张丽平.粒子群优化算法的理论及实践[D].杭州:浙江大学,2005.
[4]张增强,黄马壮.粒子群算法在计算机自动配棉优化中的应用[J].纺织学报,2011,32(2):44-47.
[5]SHI Y,EBERHART R C.Empirical study of particle swarm optimization[C].Proceedings of the IEEE Congress on Evolutionary Computation,1999:1945-1950.
[6]宋永强.改进的粒子群优化算法及其在石油性质预测中的应用[D].青岛:中国石油大学,2008:15-18.
[7]周品,赵新芬.Matlab数学建模与仿真[M].北京:国防工业出版社,2009:373-377.
[8]李宁,邹彤,孙德宝.基于粒子群的多目标优化算法[J].计算机工程与应用,2005(23):43-46.
[9]黄玉明.重钢烧结配矿优化研究[D].重庆:重庆大学,2005.
[10]周常立.烧结配料优化方法及工业应用[D].长沙:中南大学,2011.
[11]CIUPRINA G,LOAN D.Use of intelligent-particle swarm optimization in electromagnetics[J].IEEE Trans on Magnetics,2003,38(2):1037-1040.
