基于AOV图存储PLC梯形图的方法
2012-08-08张惠杰林伟敏
张惠杰,林伟敏
(福州大学 数学与计算机科学学院,福建 福州350000)
梯形图是使用最多的图形编辑语言,被称为PLC的第一编程语言。梯形图以图符的形式直观地再现了各逻辑控件的电器连接关系,并用串、并联等拓扑关系组织图符的顺序位置来表述逻辑。梯形图形象直观,但对于PLC来说是不可执行代码,无法直接运行,需事先转换成指令表。指令表是一系列符合IEC61131-3标准的指令的集合。对嵌入式PLC系统来说,研究梯形图向语句表的转换算法及其实现技术是必要的。PLC梯形图转换为指令表通常包括5个步骤[1]。参考文献[1-3]对梯形图存储结构、语法检查的规则做了详细介绍。但对梯形图的编辑没有限制,可任意绘制,从而导致处理复杂、语法检查规则繁琐。因此本文提出了直接以AOV图对梯形图进行存储的方法,编辑梯形图的同时,进行相应的规则约束,动态生成AOV图。该过程将梯形图编辑、语法检查和AOV图的生成同时完成,使常用的5个步骤缩短为3个,如图1所示。该方法与常用方法相比更为简便、快捷。
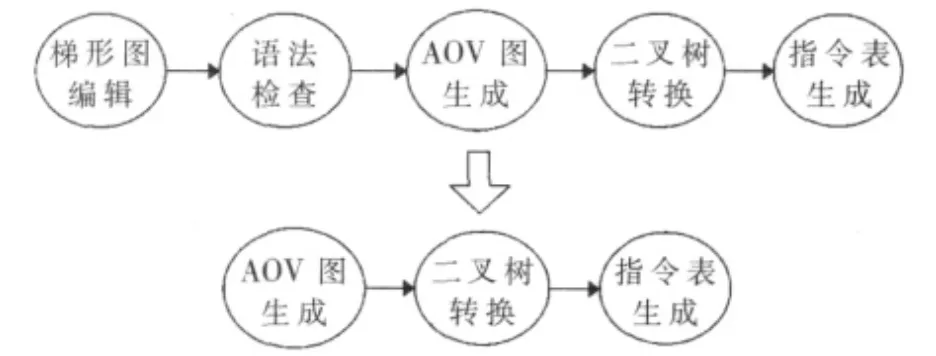
图1 PLC指令表生成过程
1 AOV图及其数据结构
AOV图是一种用顶点表示活动,用弧 PLC的梯形图程序由若干图符按一定的规则链接而成,其自上而下、自左向右的执行方式本质上就是一种AOV图,因此本文直接将梯形图中的图符以AOV图的结构进行存储,其中横线不存储,竖线存储为虚节点。如图2中上图为梯形图,下图为梯形图在内存中实际的存储结构。AOV图中普通图符有行和列两个坐标值,如X8(2,4)表示X8在梯形图中第2列第4行。虚节点有3个坐标值,分别表示虚节点的列坐标、行起始坐标和行结束坐标,如 V3(2,1,3)表示该虚节点在第 2列,起始位置为第1行,结束位置为第3行,文中规定虚节点列坐标的取值为其左边相邻位置的列坐标。 所有顶点使用一个链表进行存储,访问时对该链表进行遍历。 按照以上的对应关系,对梯形图进行修改时,其实也就是对AOV图进行修改。对梯形图的修改操作有很多:插入串联节点、插入并联节点、删除串联节点、删除并联节点、插入并联分支、插入输出分支等,如果对各种操作进行分析,根据插入、删除的各种不同情况更新AOV各个顶点的坐标,处理复杂、繁琐。因此本文提出一种直接通过AOV图拓扑结构生成AOV图各个顶点坐标的算法。该算法只需对修改后的AOV图重新进行坐标的生成,而无需理会具体的操作。算法的具体流程如下: (1)申请一个存放AOV顶点的指针堆栈、当前列坐标 CurrentX、当前行坐标 CurrentY、临时变量 x1、y1、x2、y2,AOV顶点指针为 P1、P2、P3, 并将 P1指向 AOV图中入度为0的顶点。CurrentX初始化为0,CurrentY初始化为1; (2)循环直到P1指向的节点的第一个后继节点的列坐标为11(文中描述的系统只提供11列的标记,最后一列固定为输出节点或功能块),循环过程中P1指向的节点如果为虚节点,则虚节点的列坐标设置为CurrentX,更新标记置位,若虚节点出度大于1,则将虚节点指针压入堆栈中,P1指向虚节点的第一个出度;若P1指向的节点为图符节点,则CurrentX加1,将该节点的列坐标设置为CurrentX,行坐标设置为CurrentY,更新标记置位,P1指向图符节点的后继节点。 (3)从堆栈中取出栈顶指针赋给P1,循环直至堆栈为空。循环过程中进行如下操作:①初始化变量:CurrentX设为P1指向虚节点的列坐标,P2、P3取为P1所指向的虚节点的第一个坐标未更新的后继节点,若该虚节点除了P2指向的节点外仍有未更新的后继节点,则将该虚节点的指针再次压入堆栈。②获取CurrentY的值:x1设为P1指向虚节点的列坐标,y1设为P1指向虚节点的最后一个已更新过坐标的后继节点的行坐标。如图3中,若P1指向 V1,P2指向 X8,则 x1=0,y1=1。做如下循环操作:循环直至P2指向的节点为虚节点,且虚节点的第一个后继的行坐标小于等于y1时停止;循环中P2赋值为其指向节点的第一个后继节点。循环结束后,将x2设为P2指向虚节点的列坐标。仍以X8为例,最后P2指向V5时停止,x2=5。至此获得(x1,x2)组成的区间。遍历该区间内已更新过坐标的节点,并获取这些节点中行坐标的最大值,并将CurrentY设为该最大值加1。③更新该行直至P2指向虚节点之间的节点坐标:此时P3指向P1所指向的虚节点的第一个坐标未更新的后继节点,循环直至P3指向的节点为P2指向的虚节点。循环过程中分以下几种情况进行处理:①若P3指向节点为图符节点且其后继也为图符节点,则CurrentX+1,将该节点的列坐标设置为CurrentX,行坐标设置为 CurrentY,更新标记置位,P3指向图符节点的后继节点;②若P3指向节点为图符节点,且其后继为与P3指向节点列坐标相同的虚节点,说明已更新好坐标的节点中需要插入一个新节点,某些坐标需要向右移动一个位置。此时需遍历AOV图的存储链表,寻找列坐标大于等于P3指向节点列坐标的所有虚节点,将其列坐标加1,并依次寻找这些虚节点的后继节点,沿着这些后继节点向右遍历,直至虚节点停止,将找到的后继节点列坐标加1;③若P3指向节点为虚节点,则虚节点的列坐标设置为CurrentX,更新标记置位,若虚节点出度大于1,则将虚节点指针压入堆栈中,P3指向虚节点的第一个出度。 不是所有的操作对AOV图都是有效和正确的,因此首先对AOV图的编辑进行相应的规则约束,以保证AOV图拥有正确的拓扑结构,使最后生成的梯形图符合标准,无语法错误。 对梯形图进行一些全局约束:梯形图中只提供11列元件编辑位置,最后一列固定为输出线圈或功能块。每个网络建立之后默认生成一个输出线圈,参数待用户修改。因为每个网络都必须有一个输出,其输出为输出线圈或功能块。 对AOV图(或称梯形图)的编辑只提供以下操作:添加串联开关、添加并联开关、添加输出分支、删除节点,能基本满足编辑的需要。 在完成了对AOV图的编辑后,需要将AOV图转换成二叉树,再对二叉树进行后续遍历即可获得指令表。参考文献[4-6]提出的各种基于二叉树的AOV图转换为指令表算法都无法适用于本文中的AOV图,参考文献[7]给出的方法无法适应于虚节点出度或入度大于2的情况。本文对参考文献[7]提出的算法进行了修改,使其能适用于各种AOV图向二叉树的转换。修改后的算法流程如图4所示。 (1)创建两个二叉树节点指针堆栈——“与堆栈”和“或堆栈”,分别用于保存二叉树中的“与”和“或”节点指针,并初始化两个堆栈为空。二叉树初始时为一个根节点Root,无左右子树。申请图符顶点指针P1和二叉树顶点指针P2,并将P1指向 AOV图中入度为0的顶点,P2指向 Root。 (2)从“与堆栈”中弹出“与”节点指针,并赋给 P2。 (3)创建一个“与”节点,并赋给 P3,如果 P2的左子树为空,则将 P3指向节点作为 P2的左子树,否则将 P3指向的节点作为P2的右子树。P1所指向的节点作为P3的左子树。P2新指向P3。 新建一个临时AOV图顶点指针堆栈stack,申请一个临时顶点指针tp,从P1所指顶点的第二个后继开始,做如下操作,直至最后一个后继:设当前为第OutNum个后继,将tp指向该后继。tp沿其第一个后继寻找起始行坐标小于等于P2的第OutNum-1个后继行坐标的虚节点,找到后停止。找到时如果stack为空,则将P1的第OutNum个后继和 tp压入 stack;当 stack不为空时,如果tp指向的虚节点列坐标大于等于stack的堆顶的指针所指向的虚节点的列坐标,则将P1的第OutNum个出度和tp压入 stack。 图4 AOV图转换为二叉树流程图 至此得到P1指向虚节点后继的执行顺序,越靠近stack堆顶的顶点越后执行。根据该stack建立“与”和“或”节点:从stack弹出一个图符顶点和一个虚节点,分别赋给NP和VP。新建一个“或”节点,将其赋给P4。在“与堆栈”中查找VP:①若未找到,则新建一个“与”节点,将其赋给 P3,并将 P3和 VP压入“与堆栈”中。若 P2的左子树为空,则将P3作为 P2的左子树,否则将 P3作为 P2的右子树。P4作为P3的左子树。将P4和NP压入“或堆栈”中,并将NP的压栈标志stacked置位,将P2赋给P4。②若在“与堆栈”中找到VP,则不新建“与”节点,若 P2的左子树为空,则将 P4作为 P2的左子树,否则将 P4作为P2的右子树,并将 P4和 NP压入“或堆栈”中,将 NP的压栈标志 stacked置位,将 P2赋给 P4。 循环以上操作,直至stack为空。再将P1新指向当前P1所指顶点的第一个出度。 (4)从“或堆栈”中弹出图符顶点对象赋给 P1,再弹出二叉树节点对象赋给P2;查找沿P1的支路上未建立“与”、“或”节点的后继,并为其建立“与”、“或”节点。 将P1的前驱赋给VP,计算P1在VP后继中的序号,记为OutNum。接下来的过程与步骤(3)类似,只是操作从VP的第OutNum+1个后继开始,直至第一个已入栈的后继结束,且P1也不指向顶点的第一个出度。这里不再详述。 (5)创建一个“与”节点,并将该节点赋给 P3;若 P2节点的左子树为空,则将P3指向的节点作为P2的左子树,否则将P3指向的节点作为P2的右子树;然后将P1指向的节点作为P3的左子树,并使P2指向P3对应的节点,P1新指向当前P1所指顶点的后继。因为出度小于2,所以只有一个或没有后继。 图5给出了该算法的具体实例。图5(a)为显示时所看到的梯形图程序,图5(b)为内存中实际的存储结构,图5(c)为按上述算法生成的二叉树。将图5(c)中二叉树的输出节点及其父节点去除,再去除二叉树中多余的与节点和虚节点则得到图5(d)中的二叉树,对其进行后序遍历即可得到图5(e)中的指令表。 本文提出了一种直接编辑AOV图的方法来编辑PLC梯形图,以AOV图的数据结构直接存储PLC梯形图,省去了PLC向AOV图的转换过程,且使PLC绘制过程更加便捷、规范。文中提出的AOV图坐标更新算法简化了AOV图的各种编辑情况,使其只需考虑AOV图的结构变化,而无需对节点坐标的变化进行琐碎的处理。最后文中对AOV图生成二叉树的算法进行了修改,使其可适用于各种AOV图向二叉树的转换,并给出了具体的转换实例。 [1]俞锋达.PLC编程软件的设计与下位机的仿真与实现[D].南京:东南大学,2008. [2]保慧.PLC图形化编程系统的研究与实现[D].南京:东南大学,2008. [3]葛芬.水电自动化监控系统中PLC编程工具软件的设计与实现[D].南京:南京航空航天大学,2006. [4]崔小乐,周卓岑.可编程控制器的梯形图语言与语句表语言的互换算法[J].微电子学与计算机,2000,16(l):26-30. [5]谭锦洁,程良鸿.嵌入式PLC中梯形图到AOV图的映射[J].计算机测量与控制,2004,12(10):993-995. [6]傅亮,胡飞虎,刘乐,等.基于串并联归并的 PLC梯形图向指令表转换算法[J].计算机工程与应用,2009,45(27):72-118. [7]葛芬,吴宁.基于AOV图及二叉树的梯形图与指令表互换算法[J].南京航空航天大学学报,2006,38(6):754-758.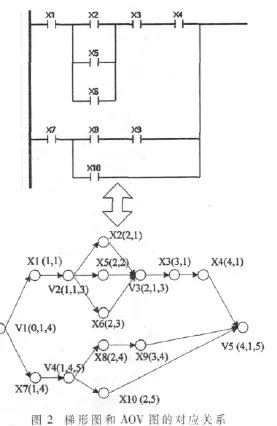
2 坐标的更新
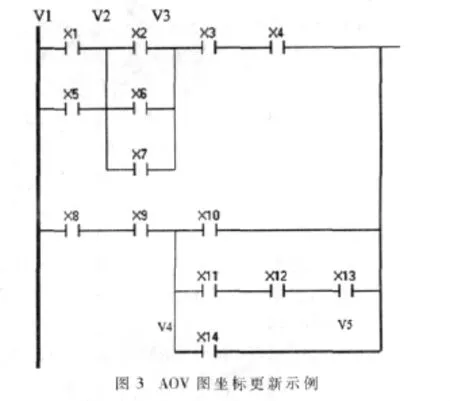
3 AOV图的编辑
4 指令表的生成


