不带利率Erlang(2)风险模型的破产时刻罚金折现期望值的拉氏变换
2012-08-07余国胜
余国胜
(江汉大学 数学与计算机科学学院,湖北 武汉 430056)
不带利率Erlang(2)风险模型的破产时刻罚金折现期望值的拉氏变换
余国胜
(江汉大学 数学与计算机科学学院,湖北 武汉 430056)
研究了不带利率Erlang(2)风险模型,得到了破产时刻罚金折现期望值的拉氏变换,给出了拉氏变换的显示表达式。
不带利率;Erlang(2)风险模型;破产时刻罚金折现期望值;拉氏变换
0 引言
经典的风险理论中索赔次数过程是泊松过程,并且经常不带利率。文献[1]讨论了常利率Erlang(2)风险模型的破产时刻罚金折现期望值。Dickson和Hipp[2]研究了不带利率Erlang(2)风险模型,得到了其破产时刻折现期望值满足一个二阶微分方程,给出了关于不带利率Erlang(2)风险模型在破产发生情形下,破产时刻矩的表达式。而不带利率Erlang(2)风险模型的破产时刻罚金折现期望值[3]的拉氏变换的讨论,有着一定的理论意义和现实意义。本文对该问题予以讨论。
1 模型
假定保险公司初始盈余为u,以每单位时间c元的速率收取保费。表示第n次索赔的时刻,Xn表示第 n次的索赔额。假定{Xn;n≥1}以及{Wn;n≥1}是独立同分布取正值的随机变量,{Xn;n≥1}的共同分布为F(x)= P(X1≤x),{Wn;n≥1}的共同密度函数为 K(t)=β2te-βt,时刻t索赔次数过程为N(t)=sup{n:Tn≤t},时刻t总索赔为了使保险公司安全运作,假设cE(Wi)>E(Xi)(i=1,2,…),则盈余过程U(t)满足

若定义破产时刻为

则盈余过程Uδ(t)的破产概率为

考虑在不带利率、破产发生的条件下,以破产前瞬时盈余和破产时的赤字为自变量的罚金折现期望值

这里I(A)是集A的示性函数,ω是一个非负有界函数,α是一个非负参数,e-αT为折现因子。
为了方便起见,引入下面的记号:
2 ϕα(u)的拉氏变换
本节约定个体索赔额服从的分布是连续型的,且有密度函数 f(x),同时记函数ξ的拉氏变换为

令文献[1]中(7)式δ=0,则有
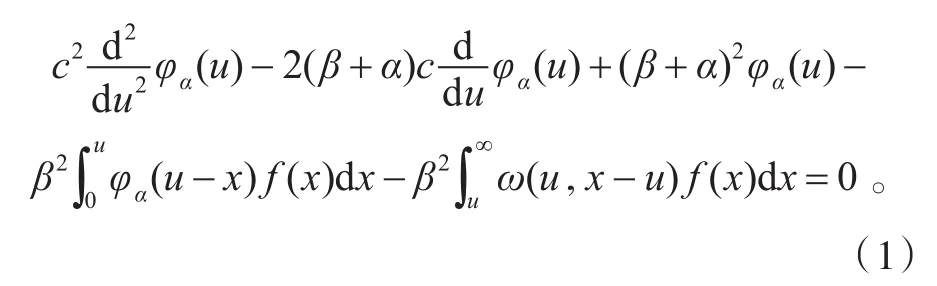
引理1[2]当α>0时,定义

注由文献[2]可得,当α→0+时,r1→0+,r2将趋于Dickson和Hipp参数,记为s0;在特定的情况下,若Lundberg基本方程除此之外还有实根,则实根取负值。
为书写方便起见,引入可积函数 f和实数r的算子Trf,定义

当r1=r2=r时,则有


将(10)式代入(7)式即知定理得证。
注①由算子Trf的性质,易见在定理1中交换r1和r2的位置后定理也成立。
②由(6)式,能将ϕα(0)用q*的形式表示。
③定理1提供了一种间接求解ϕα(u)的行之有效的方法。
[1]余国胜.常利率Erlang(2)风险模型的破产时刻罚金折现期望值[J].江汉大学学报:自然科学版,2012,40(1):17-19.
[2]Dickson D C M,Hipp C.On the time to ruin for Erlang(2)risk processes[J].Insurance:Mathematics and Economics,2001,29:333-344.
[3]程宗毛.破产时刻罚金折现期望值[J].应用概率统计,1999,15(3):225-233.
Laplace Transform of Expected Value of Discounted Penalty at Ruin in Case of Erlang(2)Risk Model Under No Interest Rate
YU Guo-sheng
(School of Mathematics and Computer Science,Jianghan University,Wuhan 430056,Hubei,China)
Considers the Erlang(2)risk model under no interest rate,in which the Laplace transform of the expected value of discounted penalty at ruin is obtained,the expression of the La⁃place transform is given.
no interest rate;Erlang(2)risk model;expected value of discounted penalty at ruin;Laplace transform
O211.6
A
1673-0143(2012)06-0008-02
(责任编辑:强士端)
2012-09-07
余国胜(1980—),男,讲师,博士,研究方向:随机动力系统、金融数学。
