一类新合成的共轭梯度算法
2012-08-07景书杰
邓 涛,景书杰
(1.信阳涉外职业技术学院,河南 信阳 465550;2.河南理工大学 数学与信息科学学院,河南 焦作 454000)
一类新合成的共轭梯度算法
邓 涛1,景书杰2
(1.信阳涉外职业技术学院,河南 信阳 465550;2.河南理工大学 数学与信息科学学院,河南 焦作 454000)
结合已有修正的DY共轭梯度方法和修正的HS共轭梯度方法的优点,提出了一种求解无约束优化问题的新共轭梯度方法,证明了该算法具有全局收敛性,同时还证明了该算法在强Wolfe线搜索下具有充分下降性。
无约束优化;混合共轭梯度法;Wolfe线搜索;全局收敛性
1 概述
共轭梯度法是求解无约束优化问题常用的最有效方法之一,相对于牛顿法和拟牛顿法,共轭梯度法具有算法简单、计算所需存储需求小等特点,因此在国防、经济、金融、工程设计、无线电通信、管理等许多优化领域都有着广泛的应用,这些领域经常会涉及到许多优化计算问题,特别是大规模优化问题,更需要一种既简单又有效的算法,因此,研究共轭梯度算法具有十分重要的意义。近年来,尽管国内外许多学者对共轭梯度法进行了深入的研究,并得到了许多研究成果[1-3],但是共轭梯度算法仍有许多值得深入研究的地方,其中包括利用不同共轭梯度算法所表现出来的良好数值属性和收敛性,利用线性组合的方法对其进行组合,得到新的共轭梯度算法。
考虑如下形式的无约束最优化问题:

其中目标函数f(x):Rn→R为光滑函数,且具有连续可微有界性。
共轭梯度算法是求解问题(1)的最有效的数值方法之一,其迭代形式如下:

其中αk>0称为搜索步长,xk为第k次迭代点,dk为搜索方向。记为梯度向量。选取搜索方向dk和步长αk的方法不同,所构成的算法也就不同。评价一个算法是否具有实用性,主要是看算法在线搜索下是否具有全局收敛性和良好的数值效果。目前所研究的搜索步长αk满足的准则(简称步长准则)主要有以下几种:
1)精确线搜索准则

2)Armijo-Goldstein准则
寻找一个αk>0,且满足下面条件:

3)弱Wolfe-Powell准则
寻找一个αk>0,且满足如下条件:

其中若αk满足(7)式和如下条件:

则叫做强Wolfe-Powell准则。
共轭梯度法是求解大规模无约束优化问题的一种有效方法,而选取不同的参数βk将对应不同的共轭梯度法,其中著名的有:

其中yk=gk+1-gk,相对应的算法分别为HS方法、FR方法、PRP方法、DY方法、LS方法。这些算法在全局收敛性和数值表现上都有各自的优缺点。Zoutendijk[4]证明了采用精确线搜索的FR方法对一般的非凸函数总是收敛的,Powell[5-6]指出PRP方法对一般的非凸函数在强Wolfe-Powell线搜索下具有全局收敛性。
戴彧红和袁亚湘[7]证明了DY方法在弱Wolfe-Powell线搜索下具有全局收敛性,但在数值结果上却不如HS方法[1-2,8]。戴彧红和袁亚湘[9]对与DY方法相关的混合梯度算法的收敛性进行了研究。近年来对于共轭梯度算法的研究又得到了新的发展,取得了很多研究成果[1-2,8-9]。
在文献[1]和文献[3]中分别给出了一种修正的HS共轭梯度公式和修正的DY共轭梯度公式:

其中μ>1,且都证明了在Wolfe-Powell搜索下的全局收敛性,文献[3]中的共轭梯度算法比DY方法具有更好的计算性和收敛性。
2 算法的提出
笔者在文献[1]和[3]的基础上,结合两者的优点,提出了一种新的共轭梯度算法:

其中 μ>1,λ为一标量。
算法(A)
步骤1 给出x0∈Rn,ε≥0,x0为初始迭代点,令d1=-g1,k:=1,如果||g1||≤ε,则停止,否则继续;
步骤2 利用弱Wolfe线搜索求步长αk;
步骤3 令xk+1:=xk+αkdk,计 算gk+1=若||gk+1||≤ε,则停,否则继续;
步骤4 根据(12)式计算βk+1,由(3)式求dk+1;
步骤5 置k:=k+1;转步骤2。
为了保证算法具有充分下降性和全局收敛性,对目标函数f(x)做出如下两个假设:
(ii)设目标函数f(x)的梯度g(x)在包含水平集Ω的闭凸集上Lipschitz连续,即存在常数L>0,使得

推论1 若假设条件(i)和(ii)都成立,则存在M>0使得

3 新公式的充分下降性
共轭梯度算法还有许多值得深入探讨的地方,其中,混合共轭梯度算法就是我们要考虑的情况之一。检验共轭梯度算法是否能表现出良好的收敛性和数值表现,且新算法能否保证算法具有充分下降性的关键在于步长αk和搜索方向dk的选取,即满足而且更希望构造的 βk满足充分下降性,即
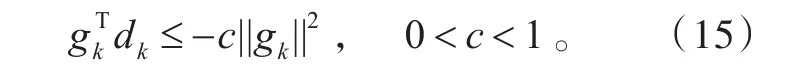
定理1 在精确线搜索条件下,若βk满足(12)式,则dk具有充分下降性,即满足(15)式。
定理2 设 x0为任给初始点,目标函数满足两个假设条件(i)和(ii),步长αk满足Wolfe-Powell搜索(7)、(8)式,则对任意的k≥1,(15)式成立。
证明当时,由(3)式得

当k=1时,结论显然成立。假设当n=k-1(k≥2)时成立,即有下面证明对于任意的 k∈N,(15)式亦成立。
根据假设及(8)式得

4 新算法的全局收敛性
引理1 若目标函数满足两个假设条件(i)和(ii),迭代序列由(2)和(3)式产生,步长αk满足(7)和(8)式,搜索方向dk满足则对任意的k∈N,有

证明由(8)式及假设(ii)得

由假设条件知,目标函数单调,从而引理1得证。
引理2 参数βk由(12)式产生,当βk≠0时,有

推论2 由引理2可知,存在一个常数b,使得

定理3 若两个假设条件(i)和(ii)成立,由(2)、(3)式产生,步长因子αk由Wolfe-Powell线搜索产生,参数βk满足(12)式,则算法或者终止于稳定点,或者

证明若gk=0对某个k成立,则xk为其稳定点,定理得证。以下用反证法进行证明。
假设定理不成立,即存在ε>0,对所有的k∈N,都有
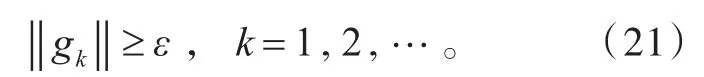
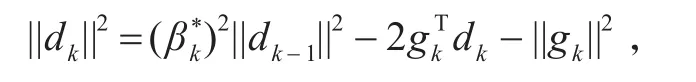
由引理1和引理2知

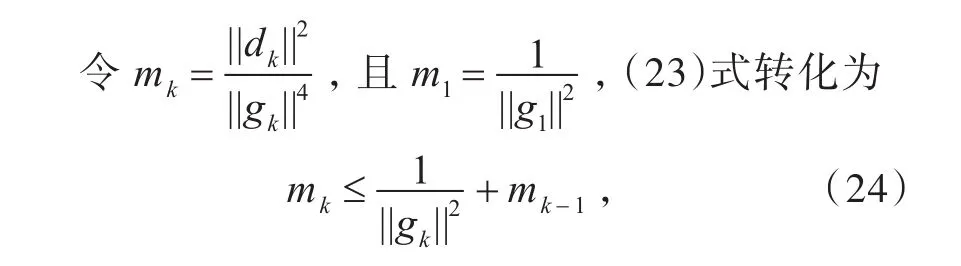
由(21)式知,对(24)式进行递推叠加得

由(25)式可得

与Zoutendijk条件矛盾,从而假设不成立,故原命题为真。
[1]王开荣,郑丽,刘金魁.两类修正的HS共轭梯度法[J].重庆工学院学报:自然科学版,2009,3(2):64-69.
[2]杨萌,王祥玲.修正HS共轭梯度法的全局收敛性[J].桂林电子科技大学学报,2009,29(3):300-302.
[3]刘金魁,王开荣.一种改进的共轭梯度法及全局收敛性[J].经济数学,2008,25(3):309-315.
[4]Zoutendijk G.Nonlinear programming,computational methods[M]∕∕Abadie J.Integer and nonlinear program⁃ming.Amsterdam,North-Holland,1970:37-86.
[5]Powell M J D.Restart procedures of the conjugate gradi⁃ent method[J].Math Program,1977(2):241-254.
[6]Powell M J D.Nonconvex minimization calculations and the conjugate gradient method[M]∕∕David F G.Numeri⁃cal Analysis:Proceedings of the 10th,Biennial Confer⁃ence Held at Dundee,Scotland,June 28-July 1,1983. Berlin:Springer-verlag,1984:122-141.
[7]戴彧虹,袁亚湘.非线性共轭梯度法[M].上海:上海科学技术出版社,2000.
[8]Hestenes M R,Steifel E L.Methods of conjugate gradi⁃ents for solving linear systems[J].J Res Nat Bur Stan⁃dards Sect,1952,49(6):409-436.
[9]Dai Y H,Yuan Y.A nonlinear conjugate gradient meth⁃od with a strong global convergence property[R].Re⁃search Report ICM95-038,Institute of Computational Mathematics and Scientific Π Engineering Computing,Chinese Academy of Sciences,Beijing,1995.
A Type of New Conjugate Gradient Algorithm
DENG Tao1,JING Shu-jie2
(1.Xinyang International Vocation Institute,Xinyang 465550,Henan,China;2.School of Mathematics and Information Science,Henan Polytechnic University,Jiaozuo 454000,Henan,China)
Combined with the existing modified DY conjugate gradient method and the modi⁃fied HS conjugate gradient method,proposes a hybrid conjugate gradient method for solving uncon⁃strained optimization problems.The strong global convergence and the sufficient descent of the new algorithm are proved in strong Wolf line search.
unconstrained optimization;hybrid conjugate gradient method;Wolfe line search;global convergence
O224
A
1673-0143(2012)06-0010-04
(责任编辑:强士端)
2011-11-02
邓 涛(1984—),男,助教,硕士,研究方向:最优化理论算法及其应用。
