电力市场需求叠加预测模型分析

黄元生 王玉玮 盖 姝 范玉凤

华北电力大学经济与管理学院 河北 保定 071003

0 引言

电能是一种特殊的商品，是现代社会所必不可少的基础能源。 在电力市场中，电力交易是最重要的一项基本行为。 因此，如何对电力交易进行科学地引导，从而使得电能的分配更加合理，这一点至关重要。本文运用叠加原理综合分析了电力需求变化的渐进性与周期性两大特点，进而引申出一种更加科学合理的组合式趋势外推技术来解决短期电力需求预测的实际问题，为电力交易提供了有力的依据与指导，从而进一步提高了我国电力市场的运转效率。

1 叠加原理思想简介

电力需求预测从内容上理解，大体可以分为两类：用电量预测与用电负荷预测。 他们归根结底都是对未来各个时段或时点上的电能需求情况进行预测，都属于随时间变化而变化的因量。 我们把具有这种随时间而变化特性的研究对象统称为时序列。

时序列一般具有两大发展特性：渐进性与周期性。传统的回归分析与趋势外推等技术往往忽略了后者，预测结果片面且不够准确。 而一些新型的智能算法技术由于其建模过程复杂，且本身采用小样本进行分析，在历史数据有限的情况下不得已而使用，其预测结果较为科学。 但是在大多数历史数据较为充分且具有明显时序列两大发展特性的情况下，本文不建议大量使用上述方法。

那么如何在预测分析的时候综合考虑时序列的两大发展特性呢？

本文认为，上述两大趋势是并存的，两者是以相加或者相乘的形式构成了一种复合式叠加模型。在预测中， 只需要分别定出这两类趋势的表达模型，再将二者相互结合起来即形成了我们所需要的预测模型。 这就是本文所要阐述的叠加原理的思想。

2 模型建立与算例分析

为简化起见，我们合理地认为电力需求时序列的渐进性发展趋势是线性的，其周期性发展趋势是季节性的即以年份为周期，周期内波动随季节而变化。 并且认为两大趋势是以相乘的方式结合的。

我们先来确定线性趋势，用如下二次平滑法：

二次平滑法又称作二次移动平均法，是随着对避免利用移动平均法预测有趋势的数据时所产生的系统误差的深入研究所发展起来的。它是在对时序列进行一次移动平均的基础上，在进行一次移动平均。 具体步骤如下：

其中，S′t为一次平均值；S″t为二次平均值；N为计算跨度值即求平均值是所选用的实际值的个数；at与bt均为二次平滑线性系数；k为预测超前期数。并取k＝－（T－1），k＝－（T－2），－1，0带入（5）式，分别求出相应的直线趋势值。

上述第（5）式即为二次平滑线性预测模型，它是在t时刻基础上对未来时序发生量的预测， 而不是在整个时段内对时序列拟合出一条直线。这是其与线性回归方法的本质区别。

根据叠加原理的思想，我们认为已知电力需求时序列严格符合乘积模型xt＝（a＋bt）Ij，因此，季节性（周期性）指数，其中Ij表示各周期内（周期为1）第j期数据与线性趋势值的比值。当数据未必严格符合模型时，用这个比值可以求出季节指数Ij。 则有

当t＝j，l＋j，∧，（m－1）l＋j时， 求出对应的It值，为了反映出个周期内同一时刻的一般规律，所以求平均值：

综上所述，用xT＋t＝（aT＋bTt）I进行预测时，取t＝j,l＋j,∧,（m－1）l＋j，则I应取Ij。

下面，就用此模型来解决实际的短期电力需求预测问题。

某地区连续四年的售电量见表1， 根据已知数据预测出该地区2012年第一季度的用电量。

表1 各季度售电量单位：万kWh

根据上表中的数据， 运用二次移动平均法原理，可建立并确定趋势模型：

将上式所计算的各季度的趋势值与各季度实际值进行比较，可以得出各季节指数，具体操作见表2。

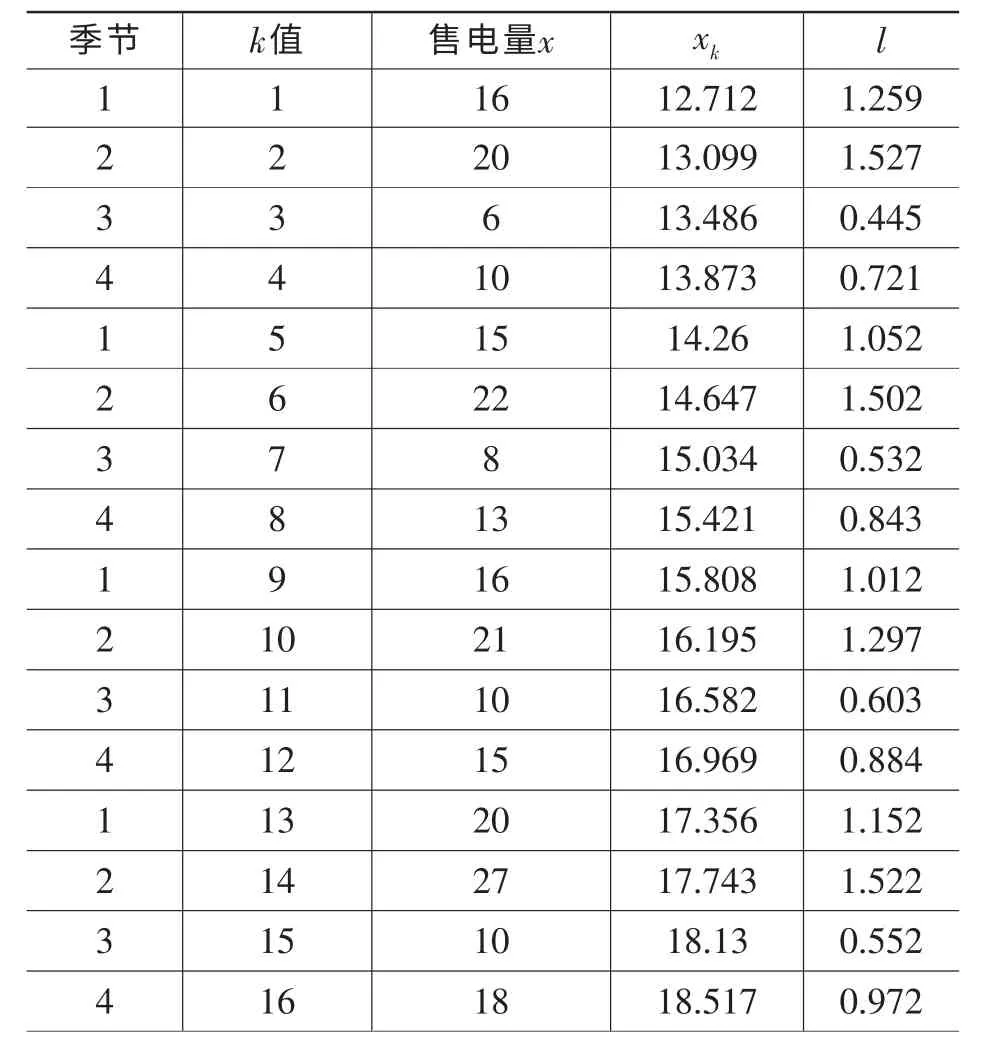
表2 季节指数对照表

对各季节性指数作均值化，规范化处理见表3。

表3 季节指数处理

上表即把四个季度对应的季节指数求出，因此最后的预测模型就是线性结构与对应的季节性指数的乘积。

将k＝17，l＝1.128带入模型，即可求出2012年第一季度的电量需求预测值，具体计算如下：

x17＝（12.325+0.387×17）×1.128＝18.904×1.128＝21.324（万kWh）

3 结论

时序列的渐进性与周期性这两大趋势的并存关系，决定了模型的建立必须是在叠加思想的基础上方能进行合理的预测。这一点在学术界已经得到了充分的证实。 在模型中除了建立乘积关系外，亦可根据实际情况建立加和关系。其具操作方法与本文类似。 本文所论述的方法，不只局限于应用在电力领域之中，在许多工程理论与实践中均可大彰其法。 这一点，望广大读者朋友能够有所收获。

［1］张守平. 电厂建设项目投资效益评价研究王婷［D］.保定：华北电力大学, 2009.

［2］李金颖. 电力市场营销学［M］.北京：中国电力出版社,2009.

［3］崔和瑞，杨丽.电力市场有效性研究［J］.华东电力，2010，（1）.

［4］刘丽萍. 发电市场稳定性影响因素分析及模糊综合评价［D］.保定：华北电力大学, 2009.