GPC算法在火炮随动系统中的仿真研究
2012-08-07王忠庆杨执中姜华杰
霍 刊,王忠庆,杨执中,姜华杰
(中北大学 信息与通信工程学院, 山西太原 030051)
0 引言
由于在战争中对火炮应用需求的不断提高,火炮随动系统对快速性和准确性有越来越高的要求。这就是要求设计的自适应控制率,不仅需要强的鲁棒性,而且算法的收敛速度要快,才能满足系统的实战要求。
近年来,随着计算机运算速度的加快和数字化技术的广泛应用,以及制造加工行业的技术更新的改进,从软硬件两个方面为把自适应控制引入火炮随动控制奠定了基础。基于不同的思路(如优化算法、系统辨识、预测控制等)的自适应控制相关研究迅速开展,目前研究的热点是如何把自适应控制与智能控制结合起来,达到更好的控制效果的方法[1-2]。
1 GPC仿真
GPC方针是基于CARIMA模型的自校正控制策略,且在其推导过程中用到了系统辨识、多步预测、滚动优化等方法,包含了自适应控制的许多优点。故而,多年前人们已开始研究如何将其用于火炮随动控制系统中。参考文献[3]提出了一种针对交磁扩大机——直流电动机模型提出的非线性广义预测控制(NGPC)算法,并对火炮随动系统受到射击干扰为4密位5步采样宽度的方波干扰的情况下,通过仿真研究证明了该方法对冲击干扰具有良好的抑制能力。本文主要研究该算法对火炮的齿隙非线性和外界不确定性干扰的控制性能即鲁棒性。
CARIMA模型可以用于存在非平稳随机扰动的情况,ξ(t)为不相关随机序列,模型为:

它的扰动仅受当前状态的影响。
GPC算法采用的是CARIMA模型和扩展预测控制的思想。具体地说,GPC控制的目标函数:
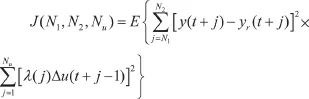
为了使GPC算法在多输入多输出(MIMO)系统应用中更加方便的调控,可在算法中引入Q、R两变量,采用:
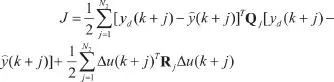
作为控制的目标函数。式中的Q、R为对角阵。并根据系统的状态方程和输出方程设计GPC算法,就可以完成在MIMO情况下的控制算法设计。按照这一方法对CARIMA模型进行仿真研究,将转速控制率与转速比环节合成后的传递函数,作为控制对象,设系统的齿隙非线性和不确定性的随机干扰,并在6 s末,受到某阶跃信号的干扰,取齿隙值为3,设采样周期为10 ms,取N2=4,Nu=1,R=0.03I,Q=100I(I为单位阵),其仿真结构如图1。可得到如图2的仿真结果。表明GPC控制对齿隙非线性和不确定性干扰具有一定的鲁棒性,可以应用于火炮随动系统控制中[3-4]。
GPC算法虽然具有很好的控制性能,但是这种方法所用到的参数较多,许多参数仍需要反复调试,比如加权因子λ(或R矩阵)的选择,就比较困难。下面给出一些简单的参数选择方法5。

图1 GPC仿真图

图2 GPC仿真结果
控制加权因子λ(或R矩阵),对快速性要求较高时应取较小的值,而对精度要求较高时应采取较大值当采样周期较大时,小的λ值会引起大的误差,控制精度降低,甚至引起大幅的极限环振荡;当采样周期较小时,控制精度大幅提高,即使存在振荡也常在误范围之内,但受运算速度和分辨率的限制。N1的选择:目前常选则N1=l; N2的选择:由于目标函数中含有未来的控制,输出长度应考虑包括受当前影响较大的所有相应段,所以N2应至少大于或等于na,nb中的较大者。 Nu的选择:一般选Nu。=l,可以避免计算中出现逆阵。若不能达到再选择更大值[6-8]。
2 结论
这里讨论的只是一般的参数选择规律,具体应该如何选择要看实际控制系统的具体要求。从以上分析可以看出,GPC控制算法对系统的非线性、不确定感染有很强的抗扰性,从而具有良好的动态特性、高的控制精度和较强的鲁棒性。然而,该方法计算复杂,许多参数如(N1、N1、λ)仍需要选择,控制率设计相对繁琐,所以可以适用于火炮随动系统等控制性能要求很高的场合。
[1]杨益群,项国波.新的ITAE最佳传递函数标准型[J].信息与控制,1997,2(2):259-265.
[2]王正林,刘明.精通MATLAB7[M].北京:电子工业出版社,2007.
[3]高元楼.火炮机电伺服系统定位精度的研究[D].西安:西安交通大学,1999.
[4]中国兵器工业第202研究所.自行高炮随动系统技术资料[Z].陕西咸阳.
[5]王正林,王胜开,陈国顺,等.MATLAB/Simulink与控制系统仿真[M].2版.北京:电子工业出版社,2008:216-223.
[6]朱新华.自行高炮全炮控制电气系统[M].石家庄:军械工程学院出版社,1999:55-56.
[7]林飞,杜欣.电力电子应用技术的MATLAB仿真[M].北京:中国电力出版社,2009:1-296.
[8]刘金琨.先进PID控制及其MATLAB仿真[M].北京:电子工业社出版社,2003:271-272.
