天生桥闸堰闸站流量定线基于MATLAB之改进

朱庆云 单延功 徐孝洪

一、基本情况

天生桥闸站位于南京市溧水县城西约5km处，是一个横跨青弋江、水阳江与秦淮河两个水系间的控制站，由江苏省水文总站于1973年设立，为省级重点水文站，具防汛、规划设计、水资源评价、灌溉、水环境调水等功能为一体。测验河段河道基本顺直（断面处河道稍有弯曲），断面呈U形状，岩石河床，无水草生长，上游距闸120m处架设过河测流手摇缆道,测流断面受闸门控制。

天生桥闸为套闸，1972年建成，单孔孔宽12.0m，闸底高程3.5 m，最大设计流量为110m3/s，实测下游最高水位11.64m（1991年7月11日）,实测最大排水流量147m3/s（2003年7月10日）。实测上游最高水位12.70m（1996年7月18日），实测最大引水流量91.5m3/s（1976年8月4日）。上游11.1km连接石臼湖,下游有武定门闸、秦淮新河闸。观测项目：流量、水位、降水量。

二、定线方法

根据堰闸形式、闸门开启情况、流态等因素按水力学基本公式分析获得不同出流情况下的水力因素与流量系数的关系方程式来推算堰闸过水流量。所采用流量公式为：

1.淹没堰流 Q=MHαΔZβ

2.淹没孔流 Q=MbeαΔZβ

式中Q为流量、M为流量系数、α和β为指数、H为水头、ΔZ为上下游水位差、b为闸孔宽度、e为闸门开启高度。

对于淹没堰流，Q=MHαΔZβ将公式变形为Q/Hα=MΔZβ，对等式两边取对数，得 Lg（Q/Hα）=βLgΔZ+LgM。

将 LgΔZ作为自变量，将 Lg（Q/Hα）作为因变量，先根据经验假定α值采用线性回归，求得β值。

将 公 式 Q=MHαΔZβ变 形 为Q/ΔZβ=MHα，对等式两边取对数，得Lg（Q/ΔZβ）=α（LgH+LgM）。

将LgH作为自变量，将Lg（Q/ΔZβ）作为因变量，根据前面获得的β值，采用线性回归，求得α值。

对于淹没孔流，可采用上述类似方法进行线形回归获得α和β值。

表1及图1、图2以2010年淹孔流量资料为例，说明了使用线性回归方法求解各待定参数的过程。（获得的拟合函数为Q=2.53Be1.001△Z0.701）

三、问题的提出

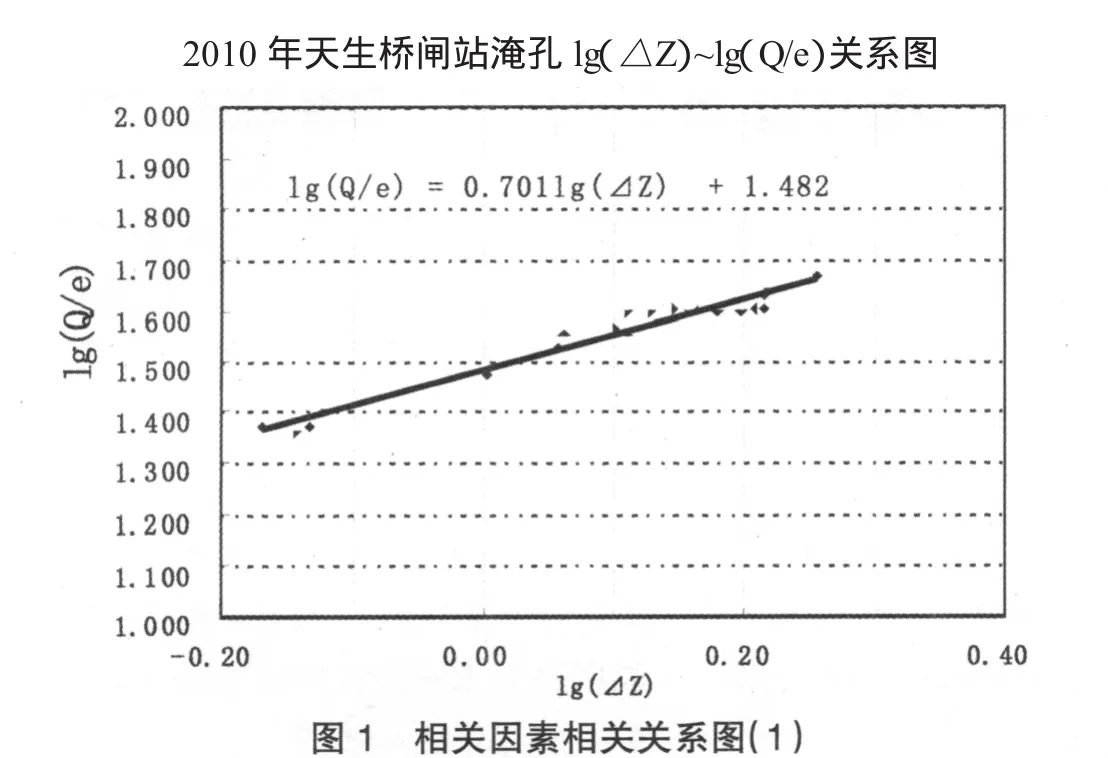
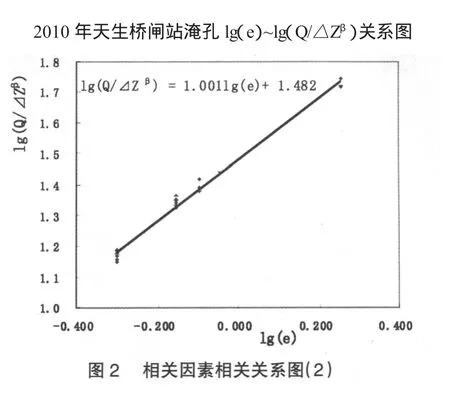
表1 淹孔流量定线计算表

如上所述，在率定待定系数时，首先根据经验为α设定一初始值，在求出β值之后，再确定α值。假定不同的α值，用相同的方法进行成千上万次迭代计算以确定最小残差平方和，对于目前这种使用excel表格率定待定系数的方法，显然是不现实的。

四、基于MATLAB的改进

为了解决这一问题，笔者编写了Matlab程序，将各个待定系数的初始值均设定为0.001,进行了10万次的迭代计算，最终输出各个待定系数以及残差平方和所需图表。

首先，编写如下程序，定义待拟合函数：

将该函数保存至Matlab的Current Directory中。然后在Matlab的Command Window中输入以下程序，调用lsqcurvefit函数进行参数优化，并输出结果以及拟合对照图：

运行后上述程序后输出结果以及实测值与拟合值对照图如下：

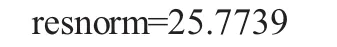
这样，所获得的拟合函数为Q=2.5192Be0.9691△Z0.6890，残差平方和为25.7739。而用excel表格拟合出的函数 Q=2.53Be1.001△Z0.701，其残差平方和为28.3435。

用Matlab程序拟合的函数其残差平方和才是最小残差平方和。

而且，这种方法的效率也不是Excel电子表格方法所能比拟的。

至于标准差和随机不确定度的计算、符号检验、适线检验和偏离检验等三项检验，按照水文资料整编规范规定执行，本文不再赘述。

五、结语

MATLAB为第四代计算机语言。目前，MATLAB被认为是工程技术人员的首选设计语言，其丰富的函数资源，简洁、直观的代码，使广大工程技术人员从C（C++）、FORTRAN、BASIC等语言冗长、烦琐的代码中得到解放，从而有更多的时间和精力放到自己的专业上