基于模糊分数阶滑模控制的永磁同步电机控制*

张碧陶 皮佑国

(华南理工大学自动化科学与工程学院，广东广州510640)

永磁同步电机(PMSM)伺服系统中的参数变化和外部负载扰动等因素影响着控制系统的性能．滑模控制技术具有对系统参数时变和外部扰动的强鲁棒性，但传统的滑模控制系统存在抖震问题［1］．比较流行的削减滑模抖震的方法主要有3种:边界层内的正侧化方法［2］、基于观测器的调节方法(利用状态观测器来观察抖震，实现滑模控制器的动态调节［3-4］)、高阶滑模控制算法［5］．这 3 种方法在一定程度上能减弱抖震，但前2种方法不具有传统滑模控制器的鲁棒性，使得系统存在稳态误差［6-7］;后一种算法复杂，在低阶(一阶或二阶)系统的控制律中存在控制器输出信号与其导数的耦合，不利于滑模控制律的设计．模糊控制虽然具有强鲁棒性且不依赖系统模型、能充分利用专家信息等优点，但模糊控制系统存在较大的静差［8］．减小模糊控制的静差的方法有:(1)细化模糊规则，但会造成规则数目“爆炸”而且效果并不明显［9-10］;(2)针对不同的误差等级采用不同分辨率的模糊集［9，11］，但是当偏差和偏差变化范围很大时，会造成计算量和存储器的花费呈指数增长;(3)在控制规则中采用3维比例－积分－微分(PID)型模糊控制器，但会降低系统的动态性能［9，12］．

针对永磁同步电机伺服系统的参数时变和外部负载扰动，文中结合滑模控制和模糊控制的优点，把分数阶微积分理论引入到控制系统中，提出了模糊分数阶滑模控制策略．模糊滑模控制系统的输入是滑模面，有利于减少常规模糊控制的静差;模糊推理输出能柔化控制作用，削减常规滑模控制的抖震．模糊滑模控制系统保持了模糊控制的不依赖系统数学模型的优点并具有滑模控制的强鲁棒性．分数阶微积分是整数阶微积分的扩展，有利于系统达到更好的控制性能．

1 永磁同步电机模型描述

永磁同步电机在旋转坐标系中的数学模型为［13］

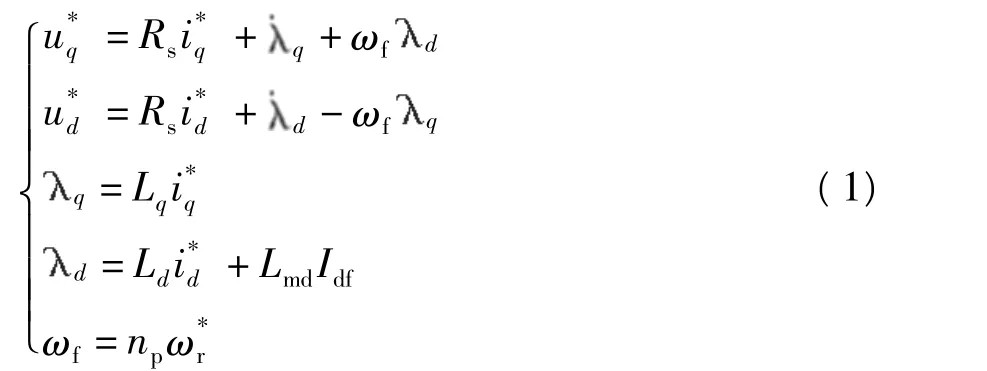
电磁转矩方程为

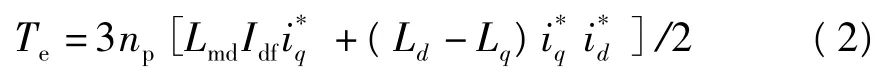
动力方程为

式中，Tl为负载力矩，Bm为摩擦系数，J为转动惯量，ωr为电机转速．

通过应用矢量控制，动力方程可以简化为

把动力方程(4)代入电磁转矩方程(2)，可得

式中，a=Bm/J，b=kp/J，c=Tl/J．

考虑电机参数变化，式(5)可以表示为

其中，Δa、Δb、Δc为系统参数摄动．

假设总的摄动满足:

2 模糊分数阶滑模控制器的设计

文中选择如下分数阶切换流形面(s):

式中:ki为滑模面增益为分数阶微分算子，t为积分上限，r为分数阶微积分，定义为

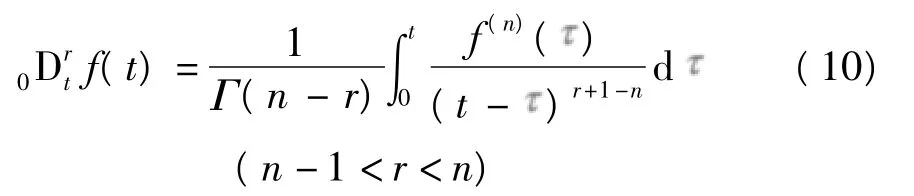
Γ(z)为Gamma函数．

采用的模糊规则为

模糊输入输出对应的推理规则和隶属度函数分别如表1和图1所示．

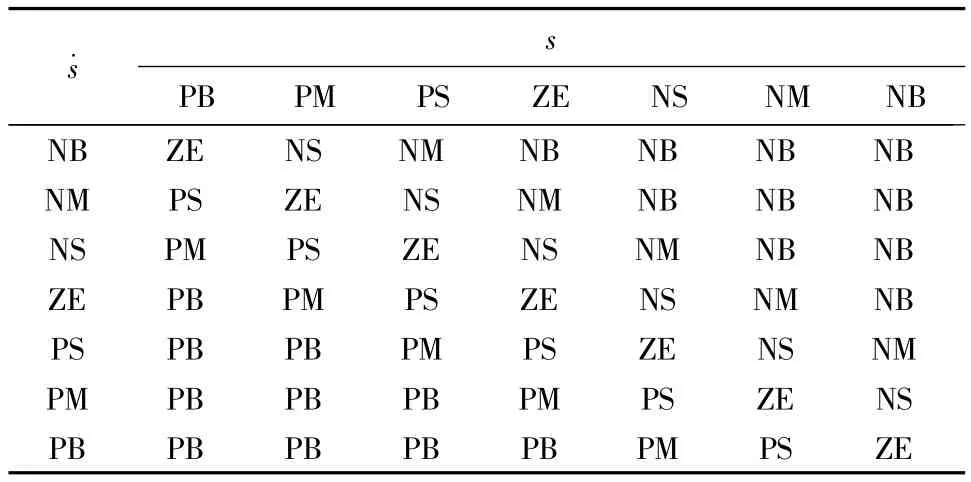
表1 模糊输入输出规则表Table 1 Rule-base of fuzzy inputs and outputs troller

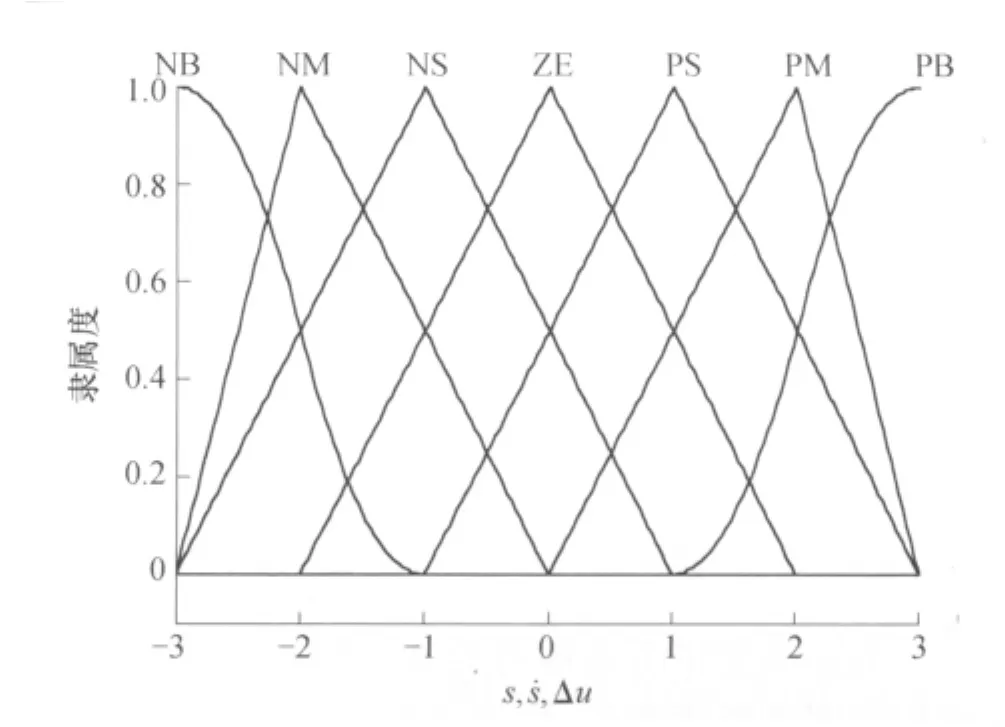
图1 模糊输入输出的隶属度函数Fig．1 Membership functions of fuzzy inputs and output

使用重心法对模糊输出Δu进行解模糊计算:

式中，kj为第j个论域的中心值．

3 系统性能分析

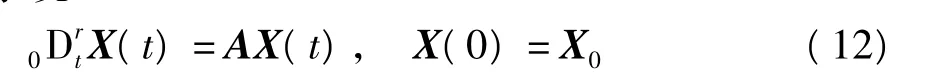
的状态稳定地收敛到零点的充要条件是

式中，arg(·)为相角，spec(A)为矩阵A的特征向量．

对于文中提出的控制系统，当系统进入滑模状态(s=0)时，有

因为ki∈R+，故有 arg(－ki) =π ＞ rπ/2．因此，分数阶滑模控制系统能稳定地收敛到零点．

分数阶方程(12)的解为

可见，整数阶系统的指数收敛性是分数阶系统的特殊形式．在分数阶系统中，可以通过调节阶数r来改变系统的收敛性，以达到更好的控制性能．

4 仿真分析

为说明文中方法的有效性，文中基于永磁同步电机伺服系统速度环，分别考察模糊分数阶滑模控制器(0＜r＜1)和模糊一阶滑模控制器(r=1)的阶跃响应及抗外部负载扰动．

文中以Matlab软件为仿真工具，采用图2所示的仿真平台．永磁同步电机参数如下:Rs=1．15 Ω，Ld=Lq=8．5 ×10－3H，np=4，J=2．5 ×10－3kg·m2，Bm=0．8 ×10－3N·m·s，ωr=1000r/min，P=1kW．

图2 永磁同步电机伺服系统仿真平台Fig．2 Simulation plant of PMSM servo system

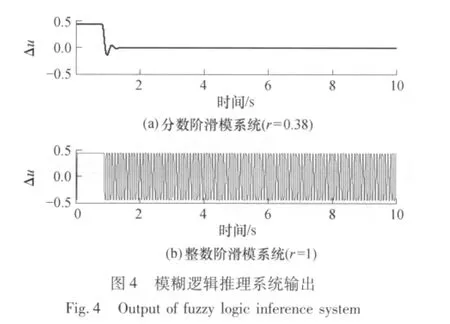
两种滑模控制系统的单位阶跃响应如图3所示，模糊逻辑推理系统的控制输出Δu如图4所示．

从图3和4可以看出，模糊分数阶滑模控制系统的抖震比常规模糊一阶滑模系统小;模糊分数阶滑模控制系统阶跃响应的稳态误差为0．系统抗外部负载扰动过程为:利用Matlab的step模块，空载运行到第12秒时，令step=0．03(突加负载)，当系统运行到第13秒时，令step=－0．03(突减负载)，仿真结果如图5所示．

从图5可以看出模糊分数阶滑模控制系统具有对外部负载扰动的强鲁棒性．图6给出分数阶导数r对系统性能的影响:随着r值的增加，系统的抖震幅值不断加大;当r减小到某值时，抖震再次加强．一般地，r在区间(0，1)内存在一个较优的值．

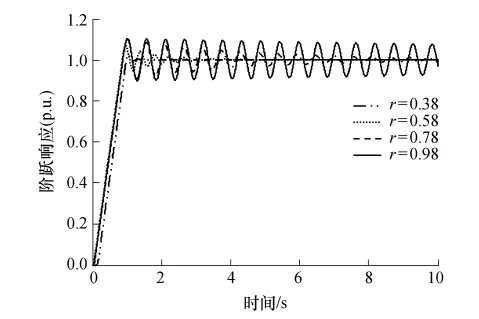
图6 r对系统性能的影响Fig．6 Effects of r on system performance

5 实验验证

采用文中提出的模糊分数阶滑模控制系统与常规模糊滑模控制系统在永磁同步电机伺服系统中进行控制性能的比较实验．此外，通过突加负载扰动实验来验证模糊分数阶滑模控制系统的抗外部负载扰动能力．PMSM伺服系统实验平台如图7所示，主控板是基于TMS320F2812的DSP处理器．PC机主要是采集伺服电机反馈回来的数据并进行分析比较．永磁同步电机主要参数同仿真实验所用参数．

图7 PMSM伺服系统的实验平台Fig．7 Experimental plant of PMSM servo system

实际伺服系统在空载时的速度环阶跃响应如图8所示，由于TMS320F2812的DSP处理器是定点DSP，图中纵坐标响应速度为标么值，而实际速度=标么值×额定转速．从图8可以看出，模糊分数阶滑模控制系统的抖震幅值比常规模糊一阶滑模系统小，实验结果与仿真结果一致．因此，文中提出的模糊分数阶滑模控制器能削减传统滑模控制系统中的抖震，达到较高的综合控制性能．

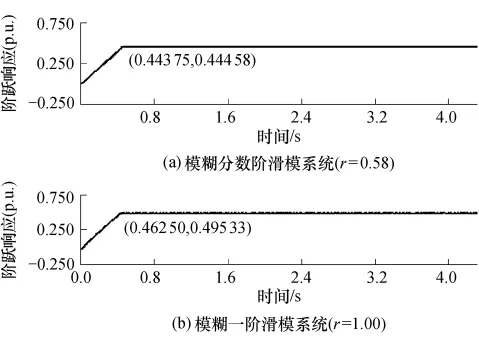
图8 两种滑模系统的速度环阶跃响应Fig．8 Speed-loop step responses of the two sliding-mode systems

图9为系统的抗外部负载扰动的鲁棒性实验结果．实验过程为:永磁同步电机带动直流发电机启动，负载电流约为0．04 A．当电机速度达到稳速400r/min并运行到第1秒时，改变变阻箱的阻值，使得负载电流约为0．12A，作用到第2秒时，再次改变变阻箱的阻值，使负载恢复到启动时的值．从图9可以看出，当系统进入滑模运动时，尽管施加3倍原负载的扰动(见图9(b))，但响应速度基本保持在恒定值(见图9(a));抗外部负载扰动实验结果与仿真结果一致．因此，模糊分数阶滑模控制系统能保持传统滑模控制系统对外部负载扰动的强抗干扰性．

图9 抗外部负载扰动的鲁棒性实验结果Fig．9 Experimental results of robustness rejecting external load disturbance

6 结语

文中针对永磁同步电机伺服系统的参数时变和外部负载扰动对系统控制性能的影响，着手解决传统一阶滑模控制系统的抖震和常规模糊控制器的静差问题，设计了模糊分数阶滑模控制系统．永磁同步电机伺服系统速度环的仿真和实验表明，文中提出的模糊分数阶滑模控制系统不但有效地削减传统滑模控制系统中存在的抖震，而且系统的输出能快速地响应指令输入并在负载扰动下保持恒定值，具有较高的综合控制性能．

［1］ 胡跃明．变结构控制理论与应用［M］．北京:科学出版社，2003:157-164．

［2］ Baik I C，Kim K H，Youn M J．Robust nonlinear speed control of PM synchronous motor using boundary layer integral sliding mode control technique［J］．IEEE Transactions on Control Systems Technology，2000，8(1):47-54．

［3］ Edwards Christopher，Spurgeon Sarah K，Patton Ron J．Sliding mode observers for fault detection and isolation［J］．Automatica，2000，36(4):541-553．

［4］ Lin Da，Wang Xingyuan．Observer-based decentralized fuzzy neural sliding mode control for interconnected unknown chaotic systems via network structure adaptation［J］．Fuzzy Sets and Systems，2010，161(15):2066-2080．

［5］ Dinuzzo Francesco，Ferrara Antonella．Higher order sliding mode controllers with optimal reaching［J］．IEEE Transactions on Automatic Control，2009，54(9):2126-2136．

［6］ Levant Arie．Homogeneity approach to high-order sliding mode design ［J］．Automatica，2005，41(5):823-830．

［7］ Boiko I，Fridman L，Castellanos M I．Analysis of second order sliding mode algorithms in the frequency domain［J］．IEEE Transactions on Automatic Control，2004，49(6):946-950．

［8］ 诸静．模糊控制原理与应用［M］．北京:机械工业出版社，1995:35-39．

［9］ 李士勇．模糊控制和智能控制理论与应用［M］．哈尔滨:哈尔滨工业大学出版社，1990:68-75．

［10］ Calcev G．Some remarks on the stability of mamdani fuzzy control systems［J］．IEEE Transactions on Fuzzy Systems，1998，6(3):436-442．

［11］ 孙庚山．工程模糊控制［M］．北京:机械工业出版社，1995:35-43．

［12］ Pedrycz Witold，Taunton Somerset．Fuzzy control and fuzzy systems［M］．New York:Research Studies Press，1993:123-134．

［13］ Lin F J，Shen P H．Robust fuzzy neural network slidingmode control for two-axis motion control system ［J］．IEEE Transactions on Industrial Electronics，2006，53(4):1209-1225．

［14］ Matignon D．Stability results for fractional differential equations with applications to control processing［C］∥Proceedings of Multi-Conference on Computational Engineering in Systems and Application．Lille:IEEE，1996:963-968．