数字轨道地图线路分段表示方法研究

夏 青，杨剑锋

（兰州交通大学 自动化与电气工程学院，兰州730070）

在基于全球导航卫星系统 （Global Navigation Satellites System, GNSS）的列车运行控制系统中，数字轨道地图不但可以校正GNSS定位误差，还可作为线路信息数据库，将列车控制集中到车载环境中，降低成本[1]。轨道地图精度越高，列车定位精度也就越高，对列车的控制也就越精确。因此，生成一份高精度的数字轨道地图是非常必要的。

大量弯曲轨道在数字轨道地图中的表示是一个难点，既要保证精度，又要考虑存储效率，不能造成数据存储量过大而影响系统的实时性。目前常用的曲线表示方法如NURBS表示会造成数据存储量过大以及地图匹配算法的复杂。折线表示法是用折线表示曲线的方法，根据精度要求确定分段数，这种方法没有将线路按照其特点进行划分，势必会增加不必要的分段，影响了数据存储效率。

铁路线路都是由直线、圆曲线、缓和曲线组成。轨道曲线的绘制，就是采集线路上若干离散点的坐标，拟合出描述轨道线形的参数，在数字轨道地图中表示出来。为了准确描述线形，需要将轨道划分为以上3种线元，再根据各个线元的特点分别拟合。该方法的关键在于准确的判断测量点位于哪一种线元上。为此，本文提出根据角度差法对线路进行划分，并给出最小二乘直线、圆曲线拟合以及缓和曲线拟合算法。

1 测量点的筛选

1.1 线路坐标系的建立与角度计算

首先建立线路直角坐标系，将测得数据转换为该坐标系下的测点坐标，测量时存在大量多余观测，因此需要从获得的测点坐标中按照一定的间隔（10或20m)提取坐标值，使得相邻2点构成的弧长相等（直线可看作半径无穷大的曲线），将提取的测量点在坐标系中标出。如图1，输入12个测量点坐标值。

设点i的坐标为（xi, yi)，则计算出点i与点i+1所形成的线段与Y轴的夹角θi为

图1中我们由上述方法分别计算出θ1到θ11的值。

图1 计算θi值示意图

1.2 线元上测量点的总体筛选

根据解析几何原理，若测点位于直线上，则点i与点i+1所形成的线段与Y轴的夹角θi值不变；若测点位于圆曲线上，则θi值的变化值△θi为一定值。根据这一性质可实现对测量点的筛选，基本思想是：

（1）计算相邻2个夹角θi与θi+1的差的绝对值△θi=|θi+1－θi|，该值为θi的变化值，如在图1中我们可以得到△θ1到△θ10；

（2） 比较相邻2个θi的变化值，看它们的差的绝对值是否小于一个给定的正常数ε（这个正常数由测量和计算误差以及轨道地图精度要求所决定），即判断△θi与ε的大小，若△θi＜ε，则认为点i、点i+1、点i+2在一条直线上，以此类推，当△θi＜ε(j>i)时，该直线段上的测点筛选结束。由此，筛选出所有直线段上的测点；

（3）当△θj＜ε时，令ai=|△θi+1－△θi，比较ai与ε值的大小，当ai＜ε时，则认为点i、点i+1、点i+2在一条圆曲线上，以此类推，当aj>ε()ji>时，该条圆曲线上的测点筛选结束。由此，筛选出所有圆曲线段上的测点；

（4）若不满足上述条件，可认为测点位于缓和曲线段上。

在实际运用时，通过设置给定正常数ε值的大小，可以减小误差并达到更加理想的轨道分段。一般计算出的圆曲线段θi的变化值△θi越大，设定的正常数ε的值相对较大可以取得更好的分段效果。

2 线元的拟合

由θi角度的变化规律，筛选出直线、缓和曲线、圆曲线的测量点，分别选取3种线元上的测点进行参数拟合计算。

2.1 最小二乘法直线拟合

设直线方程的形式为y=ax+b，获得直线线元上的坐标(x1, y1),(x2, y2),…(xk, yk)，则由最小二乘原理，则可以求得a、b的值分别为：

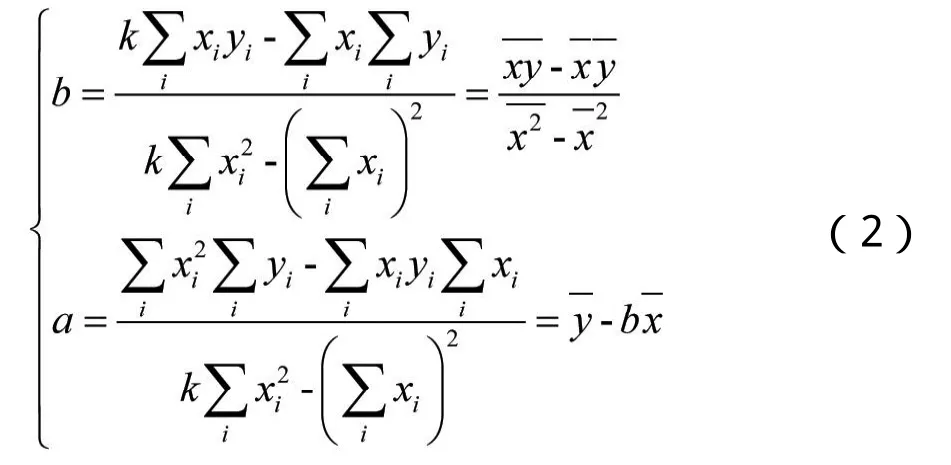
根据上式对各点坐标值进行一次计算就可求出a，b，即可得到目标直线方程。

2.2 最小二乘法圆拟合

采样圆曲线上的测点坐标(x1, y1),(x2, y2),…(xk, yk)，设R0为圆曲线半径，(X0, Y0)为圆心坐标。运用最小二乘法进行圆曲线拟合，各测点残差平方和函数为：

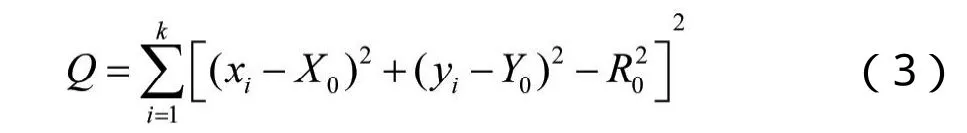
根据最小二乘法原理有：

由式（3）和（4）化简整理可得拟合出的圆曲线的半径和圆心坐标为：

由式（5）可以看出，由最小二乘法圆拟合的形式虽然复杂，但只需要对各点坐标计算一次即可得出圆曲线半径和圆心坐标，因此该算法的拟合速度是很快的。

2.3 缓和曲线的长度计算

常用的缓和曲线方程属于三次抛物线型，其表达式为：

其中：(x, y)为缓和曲线上任意一点坐标，R为圆曲线半径，l0为缓和曲线的长度。该方程的坐标原点是直缓点。

对缓和曲线采用三次多项式拟合，足以保证轨道地图的精度要求。采样缓和曲线上的测点坐标(x1, y1),(x2, y2),…(xk, yk)，拟合方程为：

只需要4个数据点的值就可确定式（7）中的a、b、c、d参数的值。

按照上述方法分别估计出铁路线路中的直线、圆曲线、缓和曲线3种线形的参数，就可以将参数存储为数字地图的形式。

3 实例计算

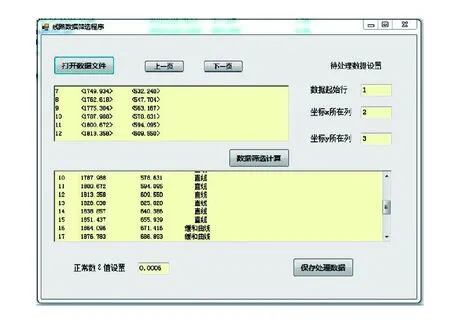
图2 线路数据筛选计算程序

按照上述算法，利用Visual C# 2005编制线路测点数据筛选计算程序，如图2。选取某一包含直线、缓和曲线、圆曲线的典型路段作算例，测量点数据按20 m等间隔提取，选取测量点数42个，程序在读取测量点的坐标数据后，能够判断出测量点所在的线元，从而大致判断出所选线路段中各线元上的测点，这里我们将ε设定为0.000 5。根据判断的结果在MATLAB下编制相应的拟合程序对3种线元进行拟合。所得的线路参数为：圆曲线半径为802.033 m；缓和曲线长度分别为110.23 m，105.06 m。对同一组数据进行多次分段拟合，并对拟合的结果进行误差校验，结果表明，拟合出的线路参数不存在较大的偶然误差和系统误差，拟合精度符合要求。图3为对不同线元拟合得到的线形。

图3 不同线元分别拟合的结果

4 结束语

本文针对铁路线路的特点，提出铁路线路分段拟合算法，根据2点确定的直线角度变化对线路进行分段，再用最小二乘原理对3种线元分别进行拟合。线路分段算法计算速度快，效率高，人工参与量少，能够准确的判断观测点数据所在的线元类型，进而准确地拟合出各个线元。相比于未作线路分段的拟合方法，可得到更加精确的线路参数，使轨道地图数据存储效率和精度得到一定的提高。应用最小二乘原理处理测量点坐标，计算过程的实质是最小二乘约束的整体优化过程，可准确恢复线路的各项参数。

[1] 张雅静，王剑，蔡伯根. 基于GNSS的虚拟应答器研究[J] . 铁道学报，2008，30（1）：104-108.