基于线性规划模型的天然肠衣原材料搭配方案

甄海燕，张 猛

(山东商业职业技术学院，山东济南 250103)

0 引言

在工程技术、经济管理、科学研究和日常生活等诸多领域中，人们经常遇到的一类决策问题:在一系列客观或主观限制条件下，寻求所关注的某个或多个指标达到最大(或最小)的决策.它们的特点就是:在若干可能的方案中寻求某种意义下的最优方案.数学上称为最优化问题，而研究处理这种问题的方法叫最优化的方法［1］.线性规划方法是最优化方法中的一种非常重要的方法，它是借助LINGO工具解决最大最小问题的一中非常简单实用的方法.天然肠衣的原材料搭配是一个线性规划问题.问题解决的方法主要是通过对不同规格肠衣的搭配、合理的降级使用以及搭配出更多最优成品捆等问题进行了分析讨论，并利用线性规划模型对肠衣搭配进行了优化，借助LINGO软件求解得出一个最优的搭配方案，这个模型不仅仅适用于天然肠衣搭配问题，它对规划类问题的求解都可以起到指导作用.

1 问题提出

天然肠衣(以下简称肠衣)制作加工是我国的一个传统产业，出口量占世界首位.肠衣经过清洗整理后被分割成长度不等的小段(原料)，进入组装工序.传统的生产方式依靠人工，边丈量原料长度边心算，将原材料按指定根数和总长度组装出成品(捆).原料按长度分档，通常以0.5 m为一档，如:3～3.4 m按3 m 计算，3.5 ～3.9 m 按3.5 m 计算，其余的依此类推.表1是几种常见成品的规格，长度单位为米，∞表示没有上限，但实际长度＜26 m.

表1 成品规格表 根

为了提高生产效率，公司计划改变组装工艺，先丈量所有原料，建立一个原料表.表2为某批次原料描述.

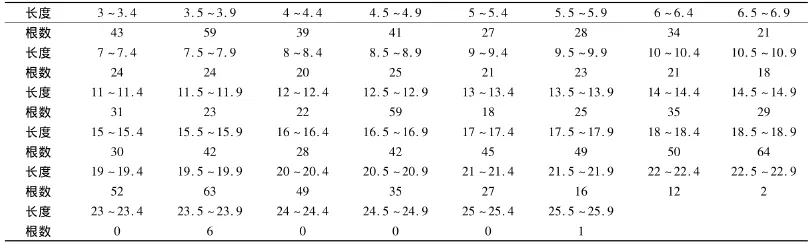
表2 原料描述表根

根据以上成品和原料描述，设计一个原料搭配方案，工人根据这个方案“照方抓药”进行生产.

公司对搭配方案有以下具体要求:

(1)对于给定的一批原料，装出的成品捆数越多越好;

(2)为提高原料使用率，总长度允许有±0.5 m的误差，总根数允许比标准少1根;

(3)某种规格对应原料如果出现剩余，可以降级使用.如长度为14 m的原料可以和长度介于7～13.5 m的进行捆扎，成品属于7～13.5 m的规格.

2 问题分析

本题根据搭配方案的3个具体要求来建立线性规划模型和优化模型;由题意知搭配方案的具体要求无先后之分.经分析，将要求(1)、(2)、(3)一起考虑，建立一个求单个规格总捆数最大的线性规划模型.在建立线性规划模型时，我们主要考虑每个规格的根数和总长度，由此建立约束条件.同时因为我们是分别求每个规格的总捆数，且考虑到要求(2)，所以，我们先求出第三个规格的总捆数，将规格三中剩余的原材料降级使用投放入规格二中，再求第二个规格的总捆数，同理，按照降级使用原则将所有剩余的放入规格一求规格一的总捆数.

3 模型假设

(1)假设工作人员输入数据的时间为零，读取结果的时间为零.

(2)假设原料测量无误差或误差较小，不会对计算与分组产生影响.

(3)假设方案产生后可立即进行组装，组装时间不会对食品保鲜产生影响.

(4)假设原料质量不会对分组、组装产生影响.

(5)第三种规格的原料如果出现剩余，可以分别降到第二种规格或第一种规格使用.

4 符号说明

模型符号说明，见表3.

表3 符号说明

5 模型建立

从题意中看出，搭配方案的三个具体要求没有先后顺序之分，故将要求(1)、(2)、(3)一起考虑.根据要求(1)，使原料数量一定的情况下，装出的成品总捆数最多，即为目标函数;整个方案的总捆数最多，即为最终的目标函数.再根据表1的数据和要求(2)“总长度允许有±0.5 m的误差，总根数允许比标准少1根”，以及每个长度段所用的总根数

不能大于其原有的总根数.由此得到模型1.

约束条件:

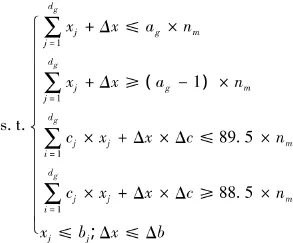
(上式中，Δx×Δc表示在上一规格的长度段中剩下的长度与段数之积的总和)同时注意，由于要求(3)“可以降级使用”，故计算时应先从规格三开始.

6 模型求解

模型已经建立完成，只要将丈量的数值代入以上的模型中，便可以得到一个符合题目要求的原料分配方案.将题目中的表1、表2的数据代入以上的模型中，求解如下:

由于要求(3)“可以降级使用”，故计算时应先从规格三开始.若原材料有剩余，则加入规格二中，成品属于规格二;若计算规格二后仍有剩余，则将所有剩余加入规格一.按此原则，求解如下:

(1)求解规格三

将规格三的数据(见表4)代入模型1中，得到:

表4 规格三数据

目标函数:

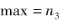
约束条件:

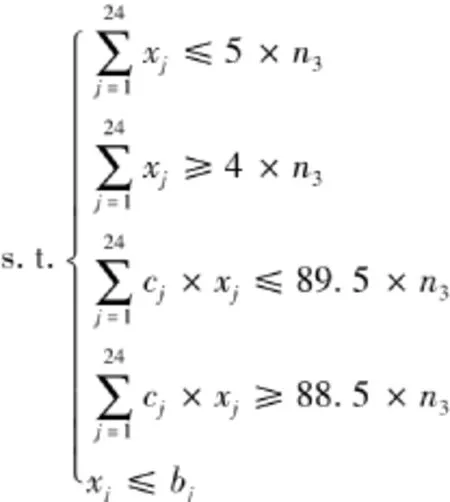
通过LINGO软件对以上线性规划模型进行求解［2］，结果为 n3=137，即规格三最多有137捆成品，xj(j=1，2，…，24)的结果见表5.

表5 规格三求解结果 根

比较表4与表5，可得到:最后剩下了2根15 m长的原材料.

(2)求解规格二

将规格二的数据(见表6)代入模型一中，得到:

表6 规格二相关数据

目标函数:

约束条件:

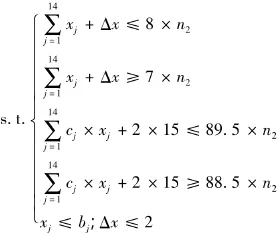
通过LINGO软件对以上线性规划模型进行求解(15 m的长度段是第25段，故程序中用x25表示Δx，表7)，结果为n2=37，即规格二最多有37捆成品，xj(j=1，2，…，14)的结果见表7.

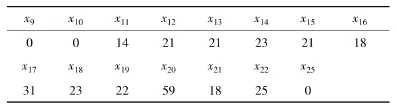
表7 规格二求解结果 根

比较表6与表7，可得到:最后共剩下了24根7 m长的、24根7.5 m 长的、6根8 m 长的、4根8.5 m长的、2根15 m长的原材料.

(3)求解规格一

将规格一的数据(见表8)代入模型一中，得到:

表8 规格一相关数据

目标函数:

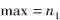
约束条件:

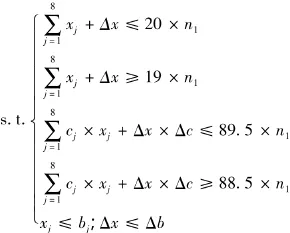
上式中，Δx×Δc表示在上一规格的长度段中剩下的长度与段数之积的总和.

通过LINGO软件对以上线性规划模型进行求解(Δx 包括 x9、x10、x11、x12、x25，5 种情况，同表 7)，结果为n1=16，即规格一最多有16捆成品，xj(j=1，2，…，8)的结果见表9.比较表8与表9，可得到:最后共剩下了6根7 m长的、24根7.5 m 长的、6根8 m 长的、4根8.5 m长的、2根15 m长的原材料.

表9 规格一求解后的结果 根

7 结语

通过对题目的解读我们不难发现这是一类规划问题.建立了一个整数线性规划模型.这个模型不仅仅适用于天然肠衣搭配问题，它对规划类问题的求解都可以起到指导作用.比如投资时，有限的资金如何分配到各种投资方式上;工厂选址时，要兼顾距离原料区和服务区的路程等这一类问题均能得到较好的解决.规划模型在工业、商业、交通运输、工程技术、行政管理等领域有着广泛的应用.

［1］王兵团.数学建模基础［M］.北京:清华大学出版社，2004.

［2］谢金星，薛 毅.优化建模与LINDO/LINGO软件［M］.北京:清华大学出版社，2005.