航空货运收益管理动态定价模型

2012-08-01周寅艳

武汉理工大学学报（信息与管理工程版） 2012年4期

周寅艳，彭怡

(南京航空航天大学民航学院，江苏南京 210016)

20世纪70年代末美国航空公司为了应对激烈的市场竞争提出了收益管理思想[1]。收益管理思想已经在航空客运、海运等领域得到了成功应用，但我国航空货运收益管理的研究才刚刚起步[2]。航空货运收益管理在综合考虑销售时间和舱位容量对决策目标，即货运供给能力收益最大化影响的基础上，通过需求预测、动态定价和舱位控制策略，能有效解决由于货运舱位价值快速流逝带来的价值易逝风险，并为航空公司带来巨大收益，其核心仍然是在合适的时间将合适的货运产品以合适的价格出售给合适的顾客[3]。

通常把航空公司看作垄断经营者，并未考虑各航空公司之间的竞争问题。然而，航空业各公司之间的竞争十分激烈，将竞争因素引入到航空货运收益管理的研究中是必然的发展趋势。国内外已有不少学者对基于竞争的客运收益管理进行了研究。BELOBABA和WILSON[4]用模拟的方法分析了只有两家航空公司在单航段市场竞争的情况。LI和OUM[5]就竞争环境下两家航空公司的舱位控制策略进行了研究，求出了完全信息下的对称均衡解。高强[6]在分析国内航空市场特点的基础上，通过构建博弈模型，研究了在竞争环境下的航空公司收益管理的舱位配置问题，但只考虑了两家航空公司舱位等级的情况。罗利和彭际华[7]建立了客运竞争市场环境下，两家航空公司的两个航班两级价格动态定价连续时间数学模型，但未分析多航段多运价的情况。汪瑜和孙宏[8]构建了竞争环境下航空客运舱位控制的博弈模型，利用拉格朗日乘数法求解各航空公司最优低价票数，并以此来确定均衡舱位。

在货运方面，目前的研究成果主要集中在理论分析和单航段或单运价收益分析上，只有少量的对多运价问题的研究。笔者结合国内航空货运的实际情况，在竞争环境下，考虑货物体积质量的二维约束特性、价格与需求之间的弹性变化以及航空公司所占市场份额，建立了多家航空公司多等级运价的货运收益管理动态定价模型，以此求得航空公司收益最大化时货运定价的均衡解。

1 问题描述及符号说明

1.1 问题描述

航空公司的收益来源分两部分:一部分来自签订合同的长期客户，具有较强议价能力;另一部分来自议价能力差的临时客户[9]。笔者研究的是在航空公司与长期客户签订的合同属于死包办协议的情况下，即在签订合同的同时已经确定了长期客户的舱位量，并且长期客户有将多余舱位转卖给临时客户的权利，会导致航空公司丢失高价临时客户的收益;同理，当长期客户需求超过协议舱位量，则长期客户就需要以高价再次向航空公司购买舱位。因此航空公司在临时客户的需求和可能溢出的长期客户需求的竞争非常激烈。在市场竞争环境下，价格的竞争直接导致需求变动，从而影响航空公司在市场中的份额。因此，航空公司必须综合考虑需求价格的弹性变化，在价格和需求间寻找一个均衡值使其收益最大化。

1.2 符号说明与基本假设

所用到的符号说明如下:

N 为航节集合，i={1，2，…，n};L为货物种类集合，j={1，2，…，l};M 为航空公司集合，m={1，2，…，m};Qki为第 k家航空公司在航节 i上的飞机腹舱的可载质量;Cki为第k家航空公司在航节i上的飞机腹舱的可载体积;为协议客户在航节i上j种货物的舱位量;为临时客户在航节i上j种货物的舱位量;为航空公司k在航节i上对于协议客户j种货物的协议舱位的单位价格;为航空公司k在航节i上对于临时客户j种货物的单位价格;为在整个航节i的运输市场中协议客户对j种货物的需求量;为在整个航节i的运输市场中临时客户对j种货物的需求量;为协议客户在航段i上j种货物需求量的体积为临时客户在航段i上j种货物需求量的体积;为航空公司与临时客户在不同种货物上的价格变动量;为临时客户在t时刻对k公司在航段i上j种货物价格为时的需求量;为临时客户在t+1时刻对k公司在航段i上j种货物价格为时的需求量。

基本假设为:

(1)航线上有m(m≥2)家航空公司共同经营，并且这些航空公司航班的起飞时刻、经停时刻和服务质量无显著差别。不考虑旅客行李及邮件所占舱位质量。

(2)为方便求解，航节的最大载运量固定，使Qki=Qk，Cki=Ck，各航节之间相互独立，无相关性。

(4)当协议客户的需求舱位大于航空公司所提供的协议舱位时，存在一部分协议客户愿意购买临时舱位来运输多余的货物，其在航节i上的意愿装载概率为αi。当航空公司与协议客户签订的协议合同在该航线上所提供的舱位大于协议客户的需求舱位时，协议客户为了减少舱位虚耗，将剩余协议舱位提供给临时客户，由于协议客户所提供的产品与航空公司提供的产品无差别，临时客户必定会转而购买协议客户提供的较低价位的舱位，直至剩余协议舱位提供完为止，才会选择购买临时舱位。

2 货运定价博弈模型

在航空公司与长期客户之间签订销售协议后，航空公司需制定合适的价格策略将合适的舱位销售给临时客户，使其收益最大化[10－11]。确定舱位的定价必须考虑市场供需情况，对任一航节i，其市场供需均存在着如下3种情况:

(1)各家航空公司所提供的协议舱位的总和小于长期协议客户需求舱位，即此时各公司的协议舱全部使用，而客户对临时舱位的需求则由两部分组成，一是临时客户的舱位需求，二是协议客户在航空公司提供的协议舱位装载满之后仍剩余部分货物未能装入协议舱位，而长期协议客户会考虑是否按照临时舱位价格将剩余货物装入腹舱或是等待下一个航班到来，将剩余货物装入。因而在此存在一个协议客户的意愿装载概率αi，即有αi的概率，协议客户愿意将货物装载入同一航班的临时舱位。基于上述情况，则第k家航空公司在航节i的收益期望为:

(2)各家航空公司设定的协议合同舱位的总和大于等于长期协议客户需求舱位但小于市场总需求，即，此时由于航空公司与协议客户签订的预留舱位是确定的，航空货运所提供的产品同航空客运一样具有易逝性，一旦航班起飞，产品立即生效，至目的地降落交付客户后失效，因而，协议客户为减少损失，将剩余舱位转卖给临时客户，但由于协议舱位提供量小于整个市场需求量，因而，没有购买到剩余协议舱位的临时客户仍旧会购买临时舱位，在该情况下，第k家航空公司在航节i的收益期望为:

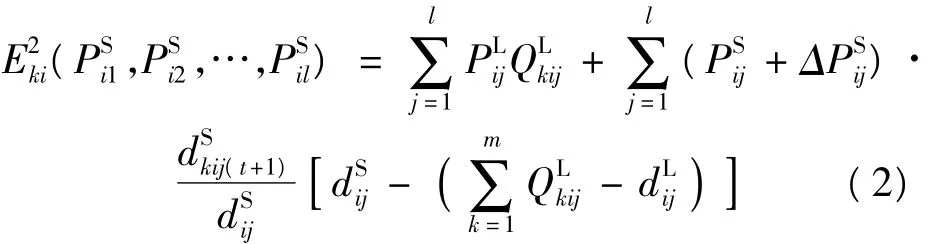
(3)各家航空公司的协议舱位提供量大于整个市场的需求量，即临时客户均能购得剩余协议舱位，航空公司获得的收益则为协议客户必须支付的协议舱位费用。此时，第k家航空公司在航节i的收益期望为:

由上可知，第k家航空公司在航节i的舱位情况只能是上述3种情况中的一种，三者不能同时存在，因而，第k家航空公司在航节i的收益期望为:由于航线上有n个航节，则第k家航空公司的期望收益为:其中，

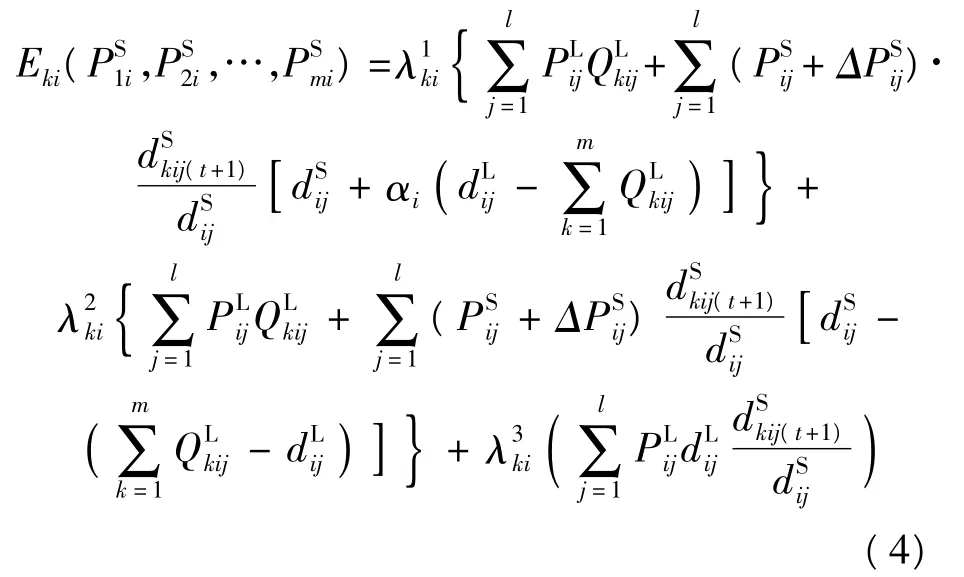
因此，取目标为第k家航空公司航班收益函数，其数学模型如下:

式(7)表示货物的质量运力约束，式(8)表示货物的体积运力约束，式(9)表示每个航段都有可分配运力。

3 求解算法

(1)确定各家航空公司在某一个航节上所占的市场份额。根据t时刻第k家航空公司的定价为PSkij以及在该定价下临时客户的需求为dSkijt，可以预测出在t+1时刻，第k家航空公司所占的市场份额其中

(2)根据货物在某航节上的质量约束和体积约束，计算出定价的可行区域。质量约束中将代入即可得到一个关于ΔPS的一元不等式。根据不同种货物的体积需求

kij换算，也可以得到一个关于的一元不等式。

(3)先假设模型符合第一种情况，根据解二次函数方程的方法求出PSkij，表示第k家航空公司采用PSkij定价策略时可以取得最大的收益。再将回溯，判断是否成立，如果成立，则此组解为所求的均衡解;若不成立，则采用第二种情况的收益期望函数，重复第一种情况的求解过程。再求得判断是否成立，若成立，则此组解为所求的均衡解。第三种情况亦如此，但在计算时可知第三种情况不存在临时客户的定价问题，因此可不做考虑。

4 数值算例

笔者选取南京—重庆—昆明的航线，该航线由3家航空公司共同经营。3家公司在该航线上所采用飞机机型均为A320，飞机腹舱最大可载质量分别为前舱3 402 kg，后舱4 536 kg，散货舱1 497 kg。假定行李邮件质量为3 000 kg，剩余最大可载质量为6 435 kg。为方便计算，令3家公司在该航线上每个航班的货物可载质量为Q1i=Q2i=Q3i=6 000 kg，飞机腹舱的可载体积为C1i=C2i=C3i=500 dm3，和转换成体积质量计算。

假设第k家航空公司在各条航线货物的价格一致，3家航空公司需求价格弹性系数分别为e1=2，e2=3，e3=4，意愿装载率 αi=0.6，其他参数如表1和表2所示。

表1 航空公司航线的协议客户定价PLij及需求

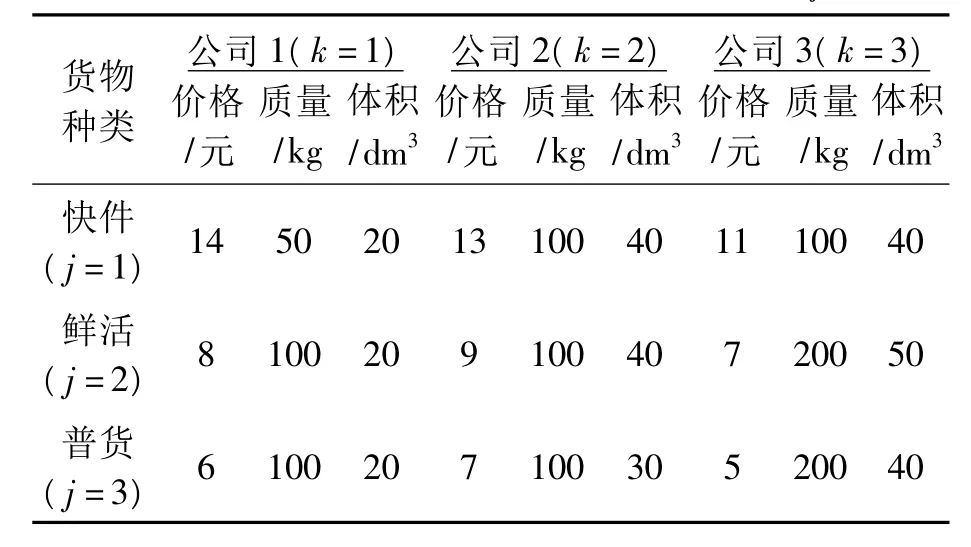
表2 航空公司航线的临时客户t时刻的定价PSijt及需求

按照求解过程采用Matlab软件进行算例编程求解，可得出航空公司的最优定价策略及其在该定价下航空公司的总收益，如表3所示。

表3 计算结果

根据伯川德价格竞争模型进行计算，当3家航空公司同时做出价格决策时，由于我国航空货运提供的服务产品相同，因此3家公司定价决策的均衡解为即他们制定相同的价格瓜分市场，同时3家航空公司获得的收益分别为 E1=5 300，E2=5 600，E3=6 000，与笔者所建模型求得的收益相当，可见笔者的模型有益于提高航空公司的收益。