免疫系统Marchuk模型的定性分析

崔 诚，王 晓，肖 莉，刘安平

(中国地质大学数学与物理学院，湖北 武汉 430074)

免疫系统的Marchuk模型是数学免疫学中一个著名模型。关于这个模型的稳定性文献[1－7]已有较多的研究，但对其振动性，特别是周期振动和几乎周期振动的讨论，除文献[8－12]外，目前尚不多见，因此，笔者就这些问题在数学理论上进行深入分析。

1 Marchuk模型

以u1、u3分别表示抗原和抗体在时刻t的浓度，u2表示等离子细胞在时刻t的浓度，由u1、u2、u3组成的微分方程组如下:

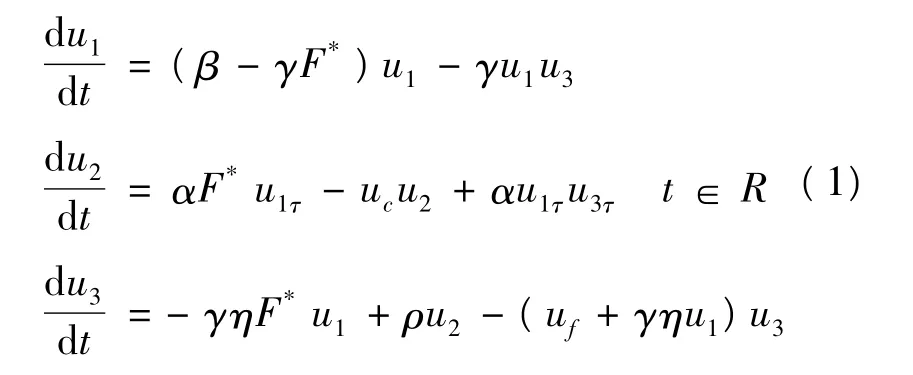
式(1)即为Marchuk模型，其中α为免疫反应系数，是t的严格正的连续函数，其余参数均为正常数，uiτ=ui(t－ τ)，τ ＞ 0，i=1，2，3。若以f1(t，u1，u3)，f2(t，u2，u1τ，u3τ)，f3(t，u1，u2，u3)分别表示式(1)右端相应的函数，则式(1)可简写为:

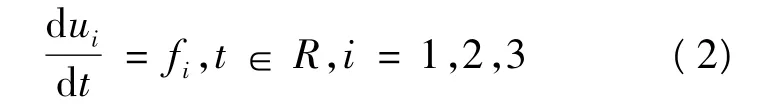
假定α(t)是T－周期或几乎周期的，则fi随α(t)关于t是T－周期或几乎周期的，从而式(1)或式(2)又称为周期或几乎周期Marchuk模型。

2 周期解和几乎周期解的存在性

不难看出，f1关于 u3单调不增，f2关于 u1τ、u3τ单调不减，f3关于u1单调不增、关于u2单调不减。由定义知fi是混合拟单调的，或说向量函数f=(f1，f2，f3)具有混合拟单调性质。

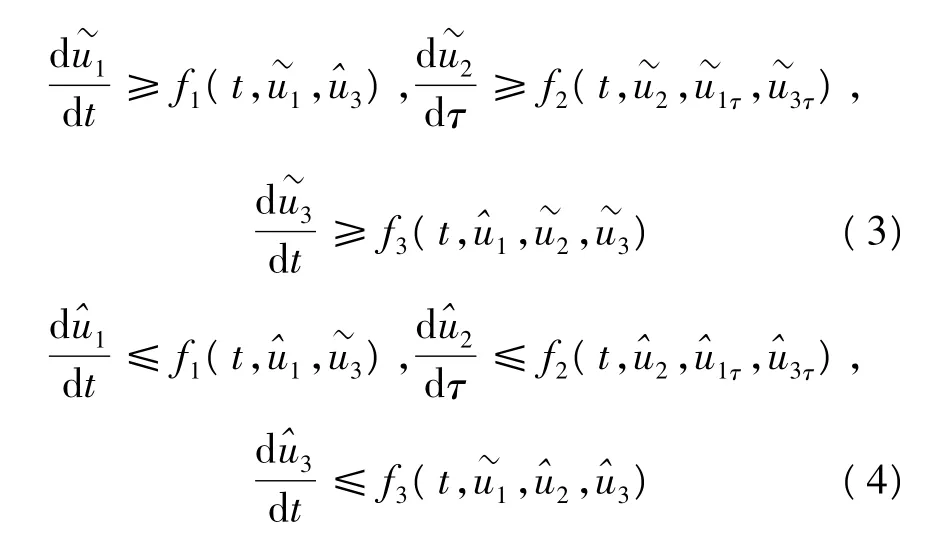
假定条件1:

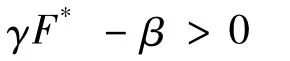
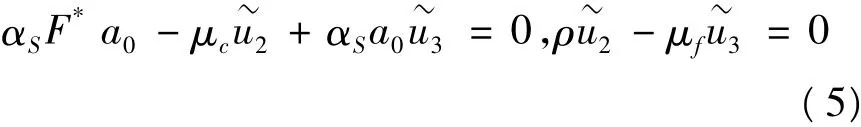
由此可得到:

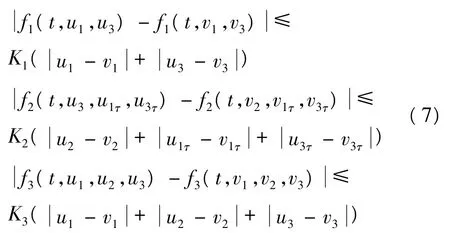
引理如果一阶线性方程:

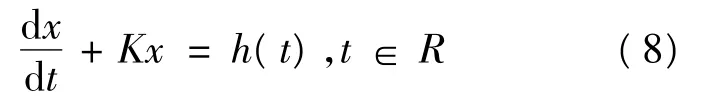
函数h(t)是连续T－周期或几乎周期的，K＞0(＜0)，则式(8)有唯一T－周期解或几乎周期解x(t)，且:

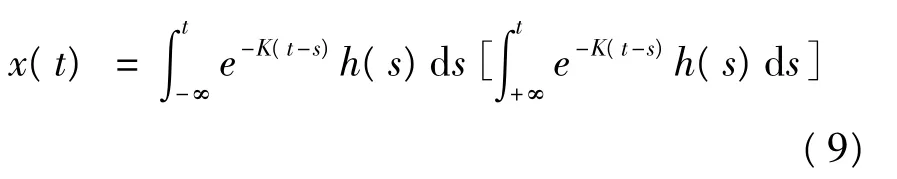
这个结论可以直接验证。

定理1设假定条件1成立，，为式(1)的一对耦合上、下解，f=(f1，f2，f3)在 Λ = ＜，＞ 上混合拟单调且满足式(7)，则式(1)存在唯一T－周期解或几乎周期解

证明先证明存在性。令B=C(R)是Banach空间，取其闭凸子集是T－周期或几乎周期的，

对任意v∈S，根据引理，可知线性方程组

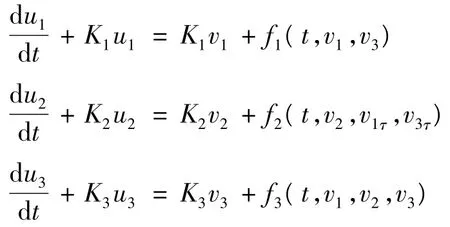
有唯一T－周期解或几乎周期解:

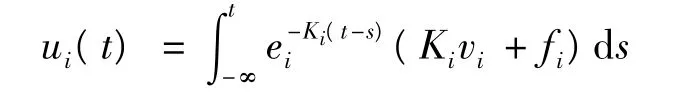
由此确定一个定义在S上的映射:

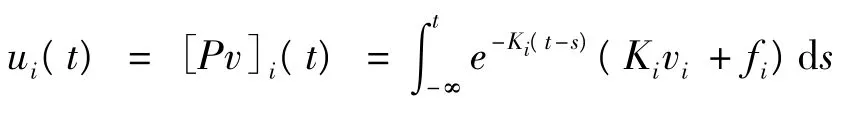
显然，P是列紧算子，再由f在Λ上的混合拟单调性有P(S)⊂S。根据schauder不动点定理，P有不动点，即u=Pu，u(t)为式(1)的T－周期解或几乎周期解，且u(t)∈＜^u，~u＞。

再证明唯一性。采用反证法，设u(t)，v(t)都是式(1)的 T－周期解或几乎周期解，由于u(t)≠v(t)，因而有 t*∈R，使 u(t*)－v(t*)≠0。令yi(t)=ui(t)－vi(t)，由式(1)有:

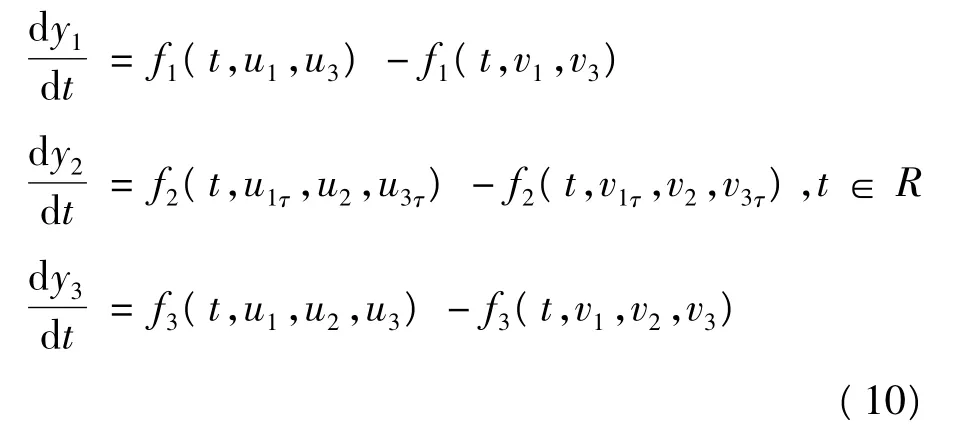
对 ε ＞0，选取充分光滑的函数 θ(t)，θ(t)=0，t≤t*，0≤θ(t)≤1，θ(t)=1，t≥t*+ ε，作如下变换:

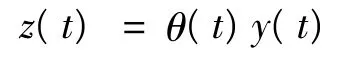
于是式(10)变为:

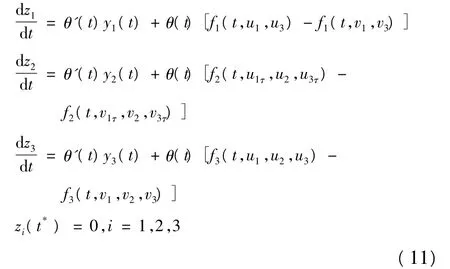
从而有:

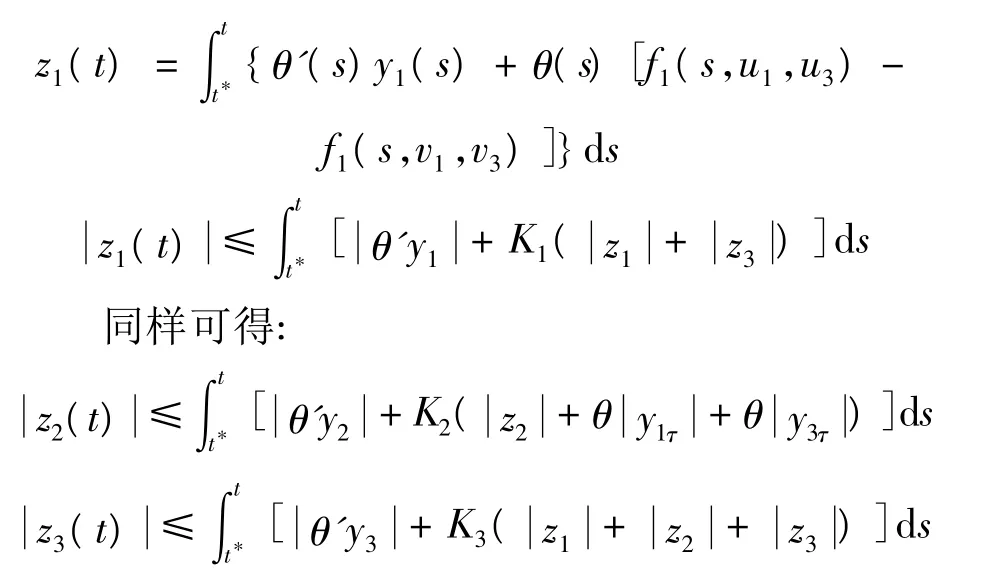
由此可得到:

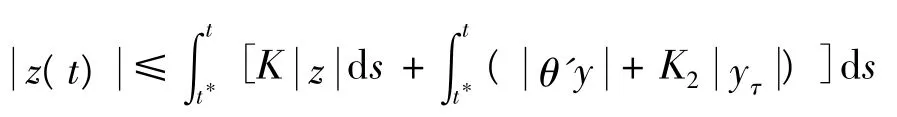
其中，K=K1+K2+K3。令 t*≤t≤t*+ ε，注意到右端第二项被积函数有界，于是有:

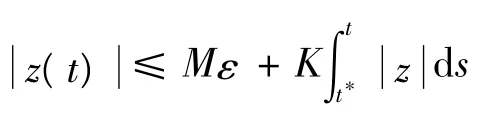
由Gronwall不等式，可得:

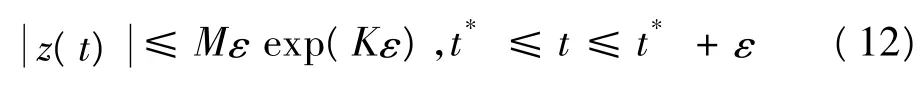
注意到z(t*1+ε)=θ(t*+ε)y(t*+ε)=y(t*+ε)=u(t*+ε) －v(t*+ε)，从而 u(t*+ε)－v(t*+ε)=u(t*)－v(t*)+u(t*+ε)－u(t*)－v(t*+ε)+v(t*)=u(t*)－v(t*)+(˙u－˙v)ε

由此并利用式(12)，可得:

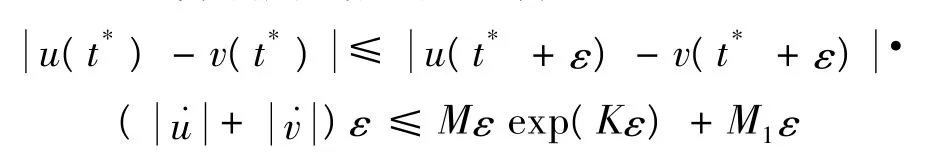
ε＞0充分小，该式表明u(t*)=v(t*)，与假设矛盾。从而唯一性成立。定理1证毕。

3 周期解和几乎周期解的稳定性

在讨论稳定性之前，先叙述定理2。

定理2若定理1的条件成立，则初值问题

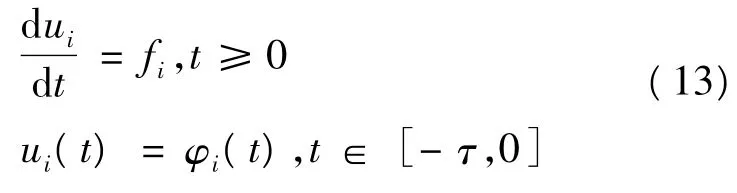
该定理的证明可由参考文献[12]中相应的定理证明方法得到。

下面讨论周期解和几乎周期解的稳定性。由于两者证明的方法相似，因而只给出周期解的证明。设u(t)为式(13)的解，u(t)为式(1)的T－周期解。令v(t)=u(t)－u(t)，且 u－u∈Λ，t∈[－τ，0]。由式(1)有:

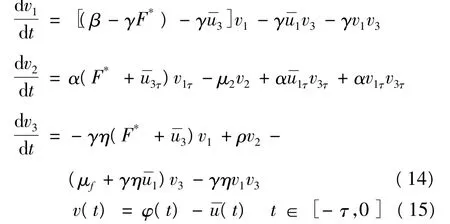
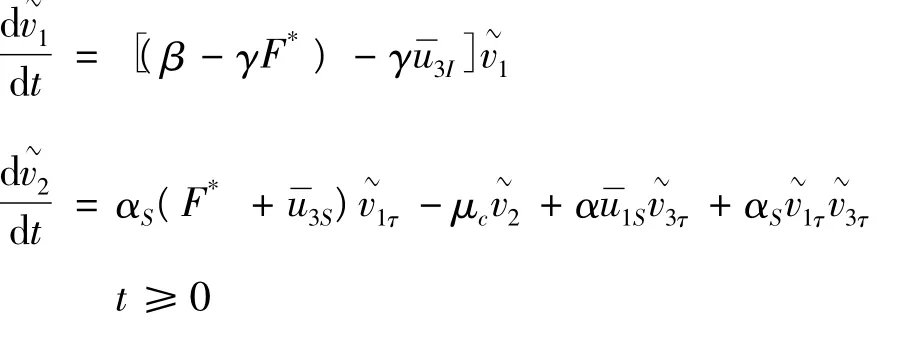
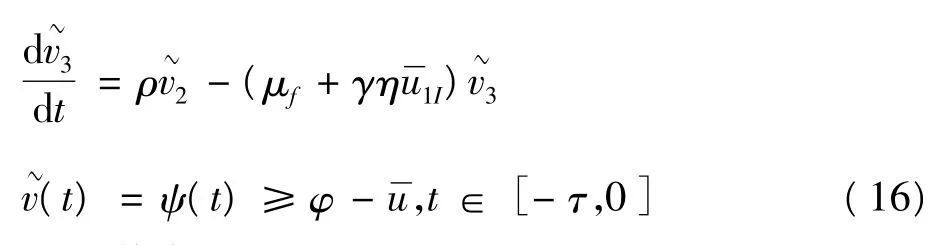
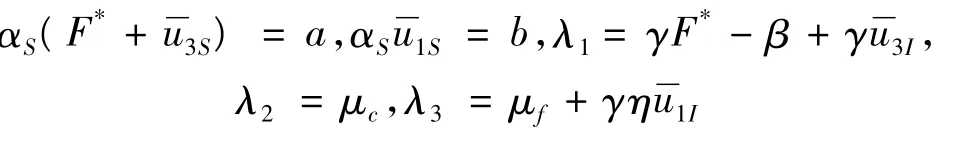
由式(16)，有:

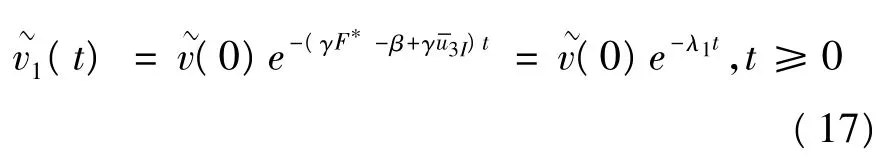
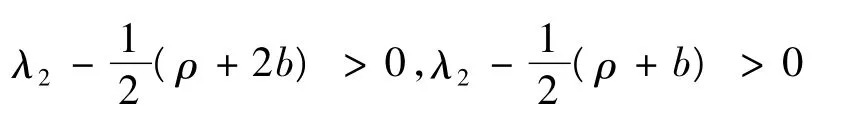
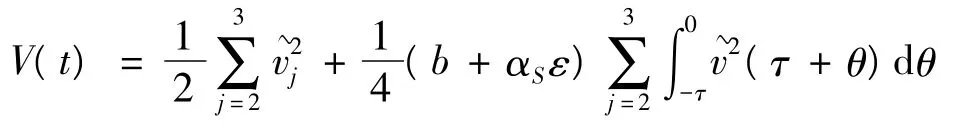
从而:

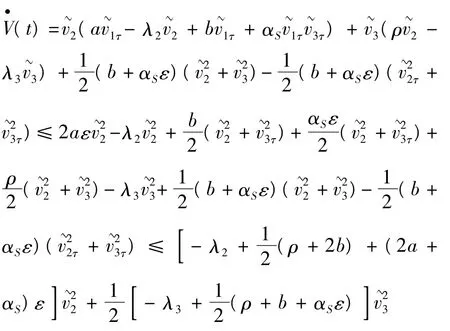
根据假定条件2，且ε＞0充分小，因此有常数 q＞0，使:

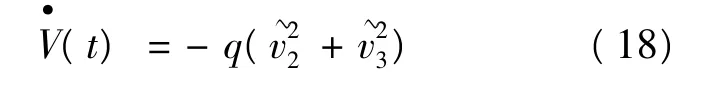
定理3如果假定条件1和假定条件2成立为式(1)的一对耦合上、下解，则其T－周期解或几乎周期解是全局渐近稳定的。

4 结论

从以上分析可以得出:免疫系统的Marchuk模型方程周期解和几乎周期解具有存在性及全局渐近稳定性。

[1] BYRNE H M.The effect of time delays on the dynamics of avascular tumour growth[J].Math Biosci，1997(144):83－117.

[2] BYRNE H M，CHAPLAIN A J.Growth of necrotic tumour in the presence and absence of inhibitors[J].Math Biosci，1996(135):187 －216.

[3] BYRNE H M，CHAPLAIN A J.Growth of non － necrotic tumour in the presence and absence of inhibitors[J].Math Biosci，1995(130):151 － 181.

[4] FORYS U.Global analysis of the initial value problem for a system of ODE modeling the immune system after vaccinations[J].Math Comp Model，1999(259):79 －85.

[5] FORYS U.Global analysis of marchuk's model in case of weak immune system[J].Math Comp Model，1997(256):97－106.

[6] FORYS U.Global analysis of marchuk's model in case of strong immune system[J].J BioL Sys，2000(4):331－346.

[7] MAGGELAKIS S A，ADAM J.Diffusion regulated growth characteristic of a spherical prevacular carcinoma[J].Bull Math Biol，1990(52):549 －589.

[8] 郑祖麻.泛函微分方程理论[M].合肥:安徽教育出版社，1994:32－98.

[9] EGAMI C，HIRANO N.Periodic solutions in a class of periodic delay prey － predator systems[J].J Math Yokohama，2004(51):45 －61.

[10] EGAMI C.Positive periodic solutions of nonautonomous delay competitive systems with weak allaee effect[J].Nonlinear Anal Real World Applications，2009(10):494－505.

[11] 施秀莲，陈树敏.一类Kdv非线性Schrodinger组合微分方程组时间周期解的存在性[J].应用数学学报，2009，32(4):577 －588.

[12] 崔诚，王晓，高飞，等.多元产品价格互惠时滞模型的周期解和几乎周期解[J].数学物理学报，2011，31(6):1718－1729.