基于增量学习的关节式目标跟踪算法*

赵运基 裴海龙

(华南理工大学自主系统与网络控制教育部重点实验室∥自动化科学与工程学院，广东广州510640)

目标跟踪广泛应用于运动识别、视频检索、交通监测、车辆导航［1］和增强实现［2］等领域．尽管针对不同跟踪目标提出了多种跟踪算法，但找到一种普遍适用的跟踪算法仍然是一个具有挑战性的课题．这主要源于目标形状和位置的变化，很难得到目标稳定的特征，同时环境光照变化、复杂的背景等给跟踪算法的自适应性能提出了挑战．

跟踪目标的特征描述直接影响跟踪算法的效果．目标的特征描述方法有空间分布颜色直方图［3］、轮廓描述［4］、混合模型的目标描述［5］和小波特征描述等［6］．近年来，子空间方法因计算简单、有效等特性而在特征提取领域得到了广泛应用．其本质是将原始的高维样本数据投影到更有利于分类的低维特征子空间．特征跟踪算法［7］首次将子空间描述［8］引入到目标特征描述领域，应用低维子空间的线性组合近似地重建训练图像，通过离线训练图像样本得到目标的低维子空间向量描述，然后应用梯度下降法进行运动参数估计．离线的图像样本训练直接影响跟踪系统的实时性，基于梯度下降法的运动参数估计经常收敛于局部的极值点．文献［9］中提出了应对目标形变和环境变化的子空间更新算法．该算法在跟踪过程中通过在线学习得到目标的特征子空间，同时在目标跟踪过程中应用粒子滤波方法代替梯度下降法实现目标运动参数估计．文献［10］中应用多元特征子空间方法处理渐变背景，实现了环境光照变化下的前景目标检测．

关节式跟踪目标描述可以通过参数化的形状和轮廓进行建模．主动轮廓的参数模型描述能力有限［11］，需要离线训练，当遇到训练过程中未出现的目标时，跟踪器的下一步跟踪将不可预测，最终影响跟踪效果．水平集合算法已成功应用到关节式目标的跟踪过程中，但该方法忽略了丰富的外观和纹理信息、目标区域中各像素点间的几何位置关系［12］．文献［13］中将位置信息引入到目标直方图描述中并成功实现了关节式目标跟踪，但目标的直方图描述中加入的位置信息相对有限．

由于跟踪目标一般选择为矩形，因此关节式跟踪目标区域无可避免地包含背景像素点．为了能准确地对目标进行描述，文中引入了图割法对目标区域进行处理，以得到目标矩形区域的前景图像(即关节式跟踪目标)．前景图像在矩形目标区域中的位置不确定性直接影响目标的特征子空间描述．鉴于二维图像快速傅里叶变换的振幅谱图像是位移不变的，文中将目标矩形区域中的前景图像用振幅谱来表示，以消除因空间位置不匹配而带来的目标描述误差．在粒子滤波框架下，将各粒子区域中前景目标的傅里叶变换幅度谱与目标基于子空间线性描述的差值作为粒子权重的描述，在跟踪过程中实时更新特征子空间向量，以实现基于增量学习的关节式目标跟踪．最后通过实验验证该方法的有效性．

1 关节式目标跟踪算法分析

1．1 跟踪目标的前景分割

假设在t时刻得到的最优跟踪目标矩形区域为Wt，当t=0时W0为初始帧中选择的目标跟踪区域，如图1所示．在目标窗口中选择3个较小的矩形窗口作为前景目标的有效逼近，最大矩形窗口为目标区域．应用积分直方图方法计算前景直方图为局部前景直方图HBtfi的线性组合，其中i(i=1，2，3)为矩形窗口的编号，其权重系数为

式中:N为直方图分辨率，文中取N=16;C(p)为像素数;k为归一化系数，以确保3个权重系数之和为1．背景直方图Hbt为整个目标区域直方图与前景直方图之差．

图1 初始帧中选取的目标Fig．1 Objects selected in initialized frames

得到背景与前景的相对准确描述之后，应用图割法对目标区域图像进行分割．图割法［12-14］定义了代价函数:

式中，E、EA、ES分别为总代价函数值、外观和形状相关的代价函数，γ为形状代价函数的权重．依据文献［13］所述，文中只考虑外观项，同时将前景密度Pf作为形状项的替代．PB为背景密度，为背景直方图的归一化值．Pi为局部前景区域Bi的密度，为的归一化值．前景密度Pf为当前的前景直方图的归一化值．根据文献［14］图割法，将式(1)转化为求代价函数(式(3))的最小值．

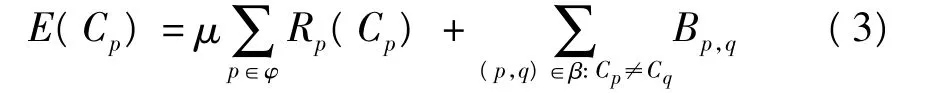
式中:φ为目标区域中的像素点集合;如果p为前景像素点，则Cp=1，否则Cp=0;μ为权重系数，文中取δ为核窗宽，I(p)为像素点p处的密度值;β为邻域像素点集合

如果 p∈Bi，则有 PF(I(p))=Pi(I(p))，否则PF(I(p))=Pf(I(p))．如果对整帧图像做处理求代价函数的最小值，那么计算复杂度会比较高，但图割法仅在目标区域内进行前景目标提取，因此对整个目标跟踪系统没有造成较大的计算负担．应用图割法实现图1中目标区域的前景检测结果如图2所示．

图2 图割算法对图1中目标区域前景检测的结果Fig．2 Results of foreground detection for target regions in Fig．1 by graph-cut algorithm

2．2 目标区域傅里叶变换的振幅谱图像

在图像处理中，一帧大小为M×N的二维图像f(x，y)的傅里叶变换可以表示为

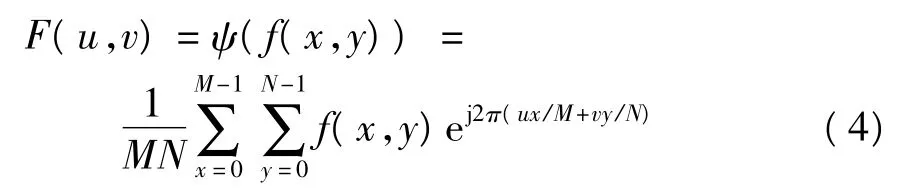
傅里叶变换具有如下的平移性质:

由式(5)可以推出

因此，二维图像的傅里叶变换的振幅谱图像具有位移不变性．文中将经图割法处理后的目标矩形区域进行二维傅里叶变换，并将其振幅谱作为目标的描述，可以消除关节式目标在目标矩形区域中因位置不匹配而对目标前景的特征子空间描述产生的影响．因此与文献［9］中直接应用矩形目标区域进行特征向量的计算相比，文中方法具有更高的跟踪准确性．图2中前景目标的傅里叶变换振幅谱如图3所示．

图3 目标区域前景的振幅谱Fig．3 Amplitude spectrum of the foreground in target region

2．3 基于增量学习的特征提取

首先离线选择训练图像集合{I1，I2，…，In}，再计算协方差矩阵的特征向量U，训练图像样本的均值中值误差矩阵奇异值分解A=UΣVT可得到特征向量U．把后续m帧{In+1，In+2，…，In+m}的跟踪结果作为目标模型的新样本对目标的特征向量进行更新．因此目标描述的特征向量更新转化为对增广中心矩阵进行奇异值分解，即对进行奇异值分解，进而得到相应的特征向量．其中IC为n+m个向量的均值，

新增加m个向量的均值为

增广中心矩阵的分块表示为

根据文献［9］可得

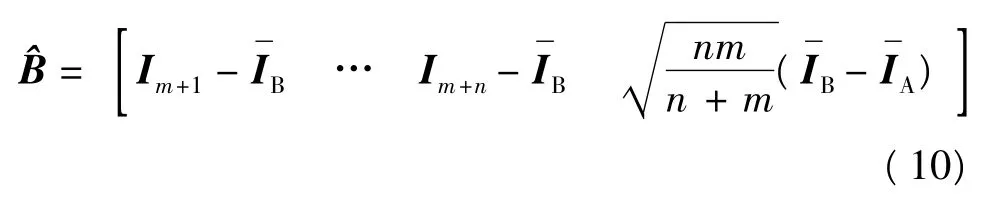
式中:f'为遗忘因子，f'∈［0，1］．由式(10)可以看出对增广中心矩阵的奇异值分解可以转换为对矩阵R的奇异值分解，进而得到增广中心矩阵的奇异值分解．目标描述的特征向量依据奇异值分解得到的特征值的大小进行选取．基于增量学习的特征提取的初始化为:训练图像集合的均值为所选初始帧图像中目标区域前景目标的振幅谱所对应的向量，集合中的元素个数为1．在基于增量学习的目标特征向量更新过程中，m=5，f'=0．9．

2．4 算法流程

在跟踪实验中，首先在第一帧图像中手动选取目标区域．在后续的图像帧中，针对粒子滤波算法［9］中粒子确定的目标区域，应用图割法对目标区域进行前景分割，对各粒子确定的区域进行快速傅里叶变换，将振幅谱转化为向量的形式，各粒子的权重由振幅谱向量与其目标线性子空间描述之间的欧式距离确定，最大权重粒子所确定的目标区域即为跟踪目标．在确定跟踪目标区域后，在分割出来的前景图像中应用全局匹配算法对Bi进行位置更新，然后进行前景直方图更新，为在下一帧图像中应用图割法进行目标前景与背景分割做准备，采用与文献［13］相同的方法对目标位置与前景直方图进行更新．在粒子滤波框架下不同时刻状态的动态模型由布朗运动进行建模，t时刻的目标状态变量由目标沿x和y轴的平移量、旋转角度、目标尺度、纵横比和扭转角组成，即 Xt=(xt，yt，θt，st，αt，φt)，t时刻的目标状态变量中，各个参数均由t－1时刻相应参数的独立高斯分布进行描述．因此，确定的矩形区域包含所有的粒子确定的目标区域，对于视频Male Skater，确定的目标位置如图4所示(最大矩形框包含了所有粒子所确定的目标位置，状态向量参数的标准差为0．005，=0．001)．在该区域中应用图割法进行目标前景分割，可有效避免各个粒子间重叠区域的重复运算．

图4 基于布朗运动的目标位置估计Fig．4 Estimation of target location based on Brownian motion

3 实验结果与分析

在Matlab环境下实现文中算法，其中包含了经过优化的Mex C++子程序．为与文献［13］中算法进行比较，实验中采用了文献［13］所提供的实验视频，该视频中图像分辨率均为320×240．同时将文中算法的目标跟踪结果与文献［9］算法的跟踪结果进行比较．所有实验均在赛扬双核CPU、2．0 GHz主频、2MB内存的计算机上实现．

图5 不同算法对不同视频序列的跟踪结果比较Fig．5 Comparison of tracking results of different algorithms for different vision sequences

如图5所示，对于视频序列Female Skater、Dancer和 Indian Dancer，文献［9，13］中算法基本上能够实现对目标的跟踪，但跟踪结果相对于实际的目标位置与文中算法相比存在较大误差．跟踪结果相对于目标实际中心位置的误差曲线如图6所示．目标实际中心位置为手动选取的矩形中心，该矩形包含目标主体部分(手和脚伸展较远部分不包括在内)．3种算法的跟踪误差的最大值、均值和标准差如表1所示．由图6和表1可知，文中算法跟踪误差的均值和方差均小于其它两种算法，文中算法的跟踪误差曲线基本上位于其它两种算法的跟踪误差曲线之下．对于视频序列Male Skater，文献［13］算法基本上能够实现对目标的跟踪，但文献［9］算法从第300帧开始逐渐丢失跟踪目标，在第350帧时跟踪目标的误差已超过了50像素，随后丢失跟踪目标，直到视频结束．文中算法实现了对目标的跟踪，而且没有发生目标丢失．图6和表1表明，文中算法相对于文献［9，13］算法具有更为精确的跟踪效果．

图6 3种算法的跟踪误差比较Fig．6 Comparison of tracking errors among three methods

表1 3种算法的跟踪误差的最大值、均值和标准差比较Table 1 Comparison of maximum，average and standard deviation of tracking error among three algorithms

跟踪算法的计算复杂度可以用其帧率表示．在文中选择的硬件和软件实验条件下，文献［9］算法、文献［13］算法、文中算法的帧率分别为 5．8、3．2、4．4f/s．在不影响跟踪精度的前提下，文中实验均选择400个粒子，随着粒子数的增加，粒子的概率密度函数逐渐逼近状态的概率密度函数，粒子滤波估计达到了最优贝叶斯估计的效果［15］．粒子数较大时文中算法对运动目标的估计更准确，但会增加计算量，因此文中算法在选择粒子数时，在参数估计精度与计算量之间做了权衡．由算法的帧率可知，文中算法与文献［13］算法相比具有更低的计算复杂度．由于前景目标的分割中引入了图割法，因此文中算法相对于文献［13］算法增加了一定的计算量．

4 结语

文中提出了一种基于增量学习的关节式目标跟踪算法．该算法应用图割法实现前景目标的提取，对提取后的前景目标进行傅里叶变换得到傅里叶振幅谱图像，对多个振幅谱图像应用奇异值分解和主元分析法实现对关节式目标的低维子空间描述．实验结果表明，文中算法具有更好的关节式目标跟踪效果和较高的跟踪精确度，同时计算量没有显著增加．文中算法对目标的局部信息考虑较少，因此在后续研究中将考虑引入目标的局部信息，实现基于整体和局部信息的关节式目标描述．

［1］ Yilmaz A，Javed O，Shah M．Object tracking:a survey［J］．ACM Computer Surveys，2006，38(4):229-240．

［2］ Puri A，Valavanis K P，Kontitsis M．Statistical profile generation for traffic monitoring using real-time UAV based video data［C］∥Proceedings of Mediterranean Conference on Control and Automation．Athens:IEEE，2007:1-6．

［3］ Birchfield S T，Sriram Rangarajan．Spatiograms versus histograms for region-based tracking［C］∥Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition．San Diego:IEEE，2005:1158-1163．

［4］ Thi Y，Vaswani N，Tannenbaum A，et al．Tracking deforming objects using particle filtering for geometric active contours［J］．IEEE Transactions on Pattern Analysis and Machine Intelligence，2007，29(8):1470-1475．

［5］ Wang Yong，Tan Yihua，Tian Jinwen．Adaptive hybrid likelihood model for visual tracking based on Gaussian particle filter［J］．Optical Engineering，2010，47(9):1-8．

［6］ Jepson A D，Fleet D J，El-Maraghi T F．Robust online appearance models for visual tracking ［J］．IEEE Transactions on Pattern Analysis and Machine Intelligence，2003，25(10):1296-1311．

［7］ Black M J，Jepson A D．Eigentracking:robust matching and tracking of articulated objects using a view-based representation［C］∥Proceedings of European Conference on Computer Vision．Cambridge:Springer-Verlag，1996:329-342．

［8］ Turk M A，Pentland A P．Face recognition using eigenfaces［C］∥Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition．Maui:IEEE，1991:586-591．

［9］ Ross D，Lim Jongwoo，Lin R，et al．Incremental learning for robust visual tracking［J］．International Journal of Computer Vision，2008，77(1):125-141．

［10］ Dong Y，De Souza G N．Adaptive learning of multi-subspace for foreground detection under illumination changes［J］．Computer Vision and Image Understanding，2011，115(1):31-49．

［11］ Kass M，Witkin A，Terzopoulos D．Snakes:active contour models［J］．International Journal of Computer Vision，1988，1(4):321-331

［12］ Zhang Tao，Freedman D．Tracking objects using density matching and shape priors［C］∥Proceedings of the Ninth IEEE International Conference on Computer Vision．Nice:IEEE，2003:1056-1062．

［13］ Nejhum S M Shaled，Ho Jeffrey，Yang Ming-Hsuan．Online visual tracking with histogram and articulating blocks［J］．Computer Vision and Image Understanding，2010，114(8):901-914

［14］ Freedman D，Zhang T．Interactive graph cut based segmentation with shape priors［C］∥Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition．San Diego:IEEE，2005:755-762．

［15］ Simon Dan．Optimal state estimation:Kalman，H-infinity，and nonlinear approaches［M］．Canada:John Wiley and Sons，2006:466-469．