基于RLS的用于贴片机贴装顺序优化的禁忌搜索算法*

罗家祥 罗树浩 吴忻生

(华南理工大学自动化科学与工程学院，广东广州510640)

表面贴装技术是一种无需在印制电路板(PCB)上钻插装孔，而直接将表面贴装元器件贴到PCB上，然后用焊料使元器件与PCB构成机械和电气连接的电子组装技术．在PCB的组装过程中，元器件的贴装是整条生产线生产效率的关键环节，是生产线上的“瓶颈”．

为减少将电子元器件贴装到PCB上所耗费的时间，提高生产效率，表面贴装技术的优化受到越来越多的关注．单台贴片机的贴装优化一般存在两个相关但仍然有一定独立性的子问题［1］:1)喂料器的位置分配问题，确定不同类型的元器件喂料器在喂料槽上的安放位置;2)元器件的贴装顺序优化问题，确定元器件的拾取和贴装顺序．前者通常被认为是一个二次分配问题(QAP)［2］，后者被认为是非对称的旅行商问题(TSP)，均属于NP难的组合优化问题．文中主要研究元器件的贴装顺序优化问题，即在喂料器安放位置确定的情况下，对元器件的拾取顺序与贴装顺序进行优化，使得贴装过程中贴装头移动的总路径最短．对该问题求解方法的研究主要集中在遗传算法和其它一些启发式算法．文献［3］中提出了具有独特的染色体编码解码方式和交叉算子的遗传算法，该算法能有效解决元器件的贴装顺序问题．文献［4］中将一种二维符号编码方法应用到遗传算法中，实现了转塔式贴片机的元器件贴装顺序和喂料槽分配的同时优化．文献［5］中针对贴装顺序优化问题建立了以贴装总时间为最小的数学模型，使用改进混合蛙跳算法来求解，结果表明该算法比遗传算法具有更好的收敛性．文献［6］在文献［5］的混合蛙跳算法的基础上，把混合蛙跳算法与蚁群算法相融合，实现对贴片机的元件贴装顺序优化问题的求解，测试结果表明混合算法取得了更小的目标函数值．此外，元器件贴装顺序优化问题的求解方法还有伞布搜索算法［7］等．

虽然遗传算法已被广泛用于求解元器件贴装顺序优化及其它复杂工业问题的优化［8］，但遗传算法具有过早收敛等局限性．为寻求更好的优化结果，文中采用基于禁忌搜索的优化算法对该问题进行求解．

首先，针对该优化问题建立数学规划模型，该模型考虑了贴装过程中贴装头的移动路径长度受贴装头间距的影响，并提出根据元器件的拾取路径求取对应最小贴装路径的方法．然后，分析了解序列的常见邻域变换方法对贴装头运动路径的影响，并据此选择了交换邻域结构;设计了包括禁忌移动和禁忌历史局部最优解的双禁忌表，避免迭代过程中相同解序列的重复更新，增强算法避免迂回搜索的能力;引入了基于取贴循环插入移动的RLS策略，参照某个参考序列来搜索以取贴循环为单位的改进的插入移动．最后，通过实验验证所提算法的有效性．

1 问题描述及数学模型

1．1 问题描述

文中研究的拱架式贴片机组成包括机架、喂料槽、喂料器、拱架、贴装头、吸嘴和视觉识别摄像机等，如图1所示．

图1 拱架式贴片机结构示意图Fig．1 Schematic diagram of surface mounting machine with overhead－gantry

同一类型的元器件一般放在相同的喂料槽上．贴片机贴装元器件的流程如下:

(1)传送带将PCB送到工作位置并夹紧固定;

(2)贴装头移动到喂料槽位置，同时或依次拾取指定的H(贴装头个数)个元器件;

(3)带着元器件的贴装头经过视觉检测区后，移动到工作台上，将元器件按指定顺序贴装到PCB上的待贴装位置;

(4)返回步骤(2)，直至PCB上的元器件贴装完毕．

从贴装元器件的流程可知，不同元器件的贴装顺序对应不同长度的贴装路径．在视觉检测时，贴装头的移动距离基本固定．因此元器件的取贴顺序是影响贴装效率的主要因素，是提高贴装效率的要点．步骤(2)和(3)实现了拾取和贴装H个元器件的过程，称为一个取贴循环．一个取贴循环包括拾取H个元器件、贴装H个元器件和返回下一个循环第一个元器件的拾取位置，如图2所示．

图2 一个取贴循环Fig．2 A picking and mounting cycle

文中拟将待贴装的元器件组成取贴循环，确定取贴循环顺序和每个循环内的元器件拾取及贴装顺序，最小化贴装头在贴装过程中移动的总路径．

1．2 数学模型

贴装头在贴装过程中移动的总路径由多个取贴循环组成，每个取贴循环中又包括了拾取、贴装元器件等多个阶段．贴装过程中的视觉检测不是贴装效率的主要影响因素，所以在优化时不给予考虑．在已知喂料器位置的前提下，元器件的拾取位置和待贴装位置均为已知条件．不失一般性，设待贴装元器件个数n为贴装头个数H的整数倍．最大限度利用贴装头时，取贴循环个数为N=n/H．设J为待贴装的元器件集合，J={1，2，…，n};S为元器件拾取顺序，S=(S1，S2，…，Sk，…，SN)，Sk为第 k(k=1，2，…，N)个取贴循环中的元器件拾取顺序，Sk=(sk，1，sk，2，…，sk，H)，该循环内贴装顺序为 Πk=(πk，1，πk，2，…，πk，H);所有贴装顺序为 Π =(Π1，Π2，…，Πk，…，ΠN); 集 合 {sk，1，sk，2，…，sk，H} ={ πk，1，πk，2，…，πk，H}，即两个集合包含的元器件相同;二维向量Ai、Bi分别为元器件i所在喂料器位置及其在PCB上的贴装位置在直角坐标系中的坐标;Δd为相邻贴装头的间距;dkj为第k个取贴循环中贴装头拾取第j与第 j+1(j=1，2，…，H －1)个元器件所移动的距离;gk为第k个取贴循环中贴装头拾取第H个元器件后移动到贴装PCB上本循环的第一个元器件所移动的距离;Dkj为第k个取贴循环中贴装头贴装第j(j=1，2，…，H－1)与第j+1个元器件所移动的距离;bk为贴装头在第k个取贴循环中贴装第H个元器件后至拾取第k+1个循环的第1个元器件所移动的距离;mk，j为第k个取贴循环中第j个贴装元器件所在的贴装头．则建立的数学模型如下:

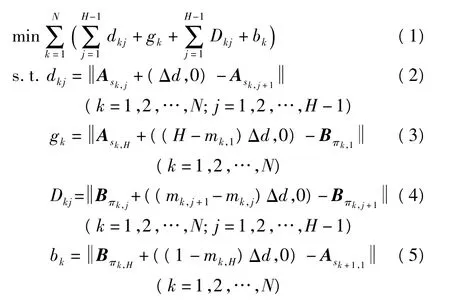
其中，· 为距离函数．目标函数(1)包括拾取元器件路径、从喂料槽到达PCB的路径、贴装元器件的路径和从PCB回到喂料槽的路径．约束(2)－(5)分别为 dkj、gk、Dkj、bk的计算式．上述模型考虑了贴装头的间距，更接近于实际贴装生产．在计算贴装头移动距离时，对每次移动的起始位置坐标进行补偿，而不是将相邻拾取或贴装的两个元器件之间的坐标距离作为移动距离，如图3所示．

图3 考虑贴装头间距时的移动距离Fig．3 Moving distance considering the space between heads

上述模型所描述的元器件拾取与贴装过程可看成一个特殊的TSP问题，因此所研究的优化问题为NP难问题．

2 求解方法

禁忌搜索(TS)算法首先由 Glover［9］提出，通过引入一个存储结构和相应的禁忌准则来避免迂回搜索，并通过藐视准则来赦免一些被禁忌的优良状态，保证了多样的有效搜索，已成功地解决了各类经典的优化问题．文中从TS算法的组成要素入手，结合贴片机贴装顺序优化问题的特点，提出了一种基于参考解的局部搜索(RLS)的改进TS算法，设计了包括传统禁忌表与历史解禁忌表的双禁忌表来避免迂回搜索，以提高搜索的多样性．同时设计了基于取贴循环插入移动的RLS局部搜索策略，以提高算法的搜索性能．

2．1 解的表达形式及特点

一个取贴循环主要包括拾取和贴装两个过程，显然元器件的拾取顺序与贴装顺序是不一定相同的．在模型描述中，已用 S=(S1，S2，…，Sk，…，SN)和 Π =(Π1，Π2，…，Πk，…，ΠN)表示取贴循环中的元器件拾取序列和贴装序列，两者可进一步分别用长序列 S=(s1，s2，…，sH，…，sH(k－1)+1，…，sHk，…，sn)和 Π =(π1，π2，…，πH，…，πH(k－1)+1，…，πHk，…，πn)表示，并满足{sH(k－1)+1，…，sHk}={πH(k－1)+1，…，πHk}的条件，表示第k个取贴循环内拾取的元器件与贴装的元器件相同．

对于第k个取贴循环中贴装顺序Πk的改变，只影响本循环的路径总长度，不影响其它循环．因此，可以在不影响其它循环的前提下，寻找一个循环内的最优贴装顺序，使得本循环的贴装总路径长度最小．在Sk确定的条件下，最优的Πk为:以本循环拾取的最后一个元器件sHk为起点、下一循环拾取的第一个元器件sHk+1为终点共H+2个城市的小规模TSP问题的解，如图4所示．

图4 单循环内最优贴装顺序Fig．4 Optimal mounting sequence in a single cycle

因此，求解所研究的优化问题可集中在拾取序列S，而S对应的贴装顺序可通过若干个小规模的TSP问题的求解获得．贴装顺序的求解可在计算对应拾取序列的目标值时进行．

2．2 初始解的产生

文中基于最近邻的启发式方法［10］来获取拾取顺序的初始解．按最近邻原则，分3个阶段逐步确定当前取贴循环内的元器件拾取顺序、当前循环内的元器件贴装顺序、下一循环拾取的第一个元器件．设Ω=J={1，2，…，n}，为待拾取的元器件集合，第 k个循环内的元器件拾取顺序为 Sk=(sH(k－1)+1，sH(k－1)+2，…，sHk)，贴装顺序为 Πk=(πH(k－1)+1，πH(k－1)+2，…，πHk)，c1，i，j为贴装头从拾取元器件 i移动到拾取元器件 j所经过的距离．c2，i，j为贴装头在PCB上从贴装元器件i移动到贴装元器件j所经过的距离;c3，i，j为贴装头从拾取元器件 i移动到贴装元器件j所经过的距离;c4，i，j为贴装头从贴装元器件 i移动到拾取元器件 j所经过的距离．c1，i，j、c2，i，j、c3，i，j、c4，i，j(i，j=1，2，…，n)可通过已知喂料器和贴装点的坐标计算得到．产生初始解的具体步骤描述如下:

(1)令 k:=1，在 Ω 中任意选择元器件 i，sH(k－1)+1:=i，Ω:= Ω /{i};

(2)对所有 h(h=2，3，…，H)，在 Ω 中选择 i=

(4)对所有 h(h=2，3，…，H)，在 Ψ 中选择 i=

2．3 邻域

交换、插入、2－opt和 3－opt是常见的邻域结构，常应用于搜索算法中．当对解序列中的1个或2个元器件移动时，插入、2－opt和3－opt移动会使得多个取贴循环发生改变，导致当前解结构产生较大变化，搜索的随机性太强．因此，文中算法采用交换邻域．在解序列中选择两点，然后交换在解序列中的位置，得到一个新的邻解，如图5所示．对解序列中任意两点进行交换，得到的所有解构成交换邻域．

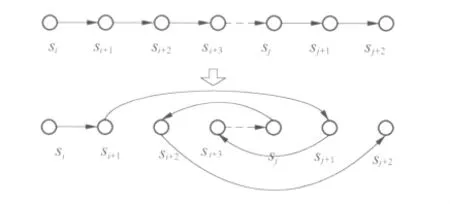
图5 交换移动示例Fig．5 An example of exchange move

与其它移动相比，交换移动只改变交换的两个点所在的取贴循环内元器件的拾取顺序，对其余的循环没有影响．此外，由于同一循环内元器件的拾取按一个方向进行，可避免贴装头在喂料槽上来回移动，使得该循环的拾取总路径最小，因此解序列中同一循环内的两个元器件交换意义不大．由此可知，对于取贴循环总数N和循环内贴装元器件总数H，有效的交换邻域大小为

2．4 禁忌表

文中提出的TS算法采用双禁忌表TL1和TL2，禁忌表TL1记录交换移动，禁忌表TL2记录历史解．

2．4．1 禁忌表 TL1

在TS算法中，为避免迂回搜索，一旦一个移动被接受，它的反移动就会被记录到表中，在此后固定迭代步长内该反移动会被禁忌．对于交换邻域结构，禁忌表TL1中的禁忌对象为交换的两个点，而禁忌表长度根据问题的规模而定．

2．4．2 禁忌表 TL2

虽然禁忌表TL1在一定程度上可避免迂回搜索，但对于统治性较强的局部最优解，算法可能会在若干次迭代后再次陷入该解，所以TL1不能保证完全杜绝迂回搜索现象．若盲目地增大禁忌表的长度，不仅会削弱禁忌表的作用，而且会导致TS算法的性能因禁忌太多而变差．

由序优化理论［11］可知，在解空间中均匀抽取v个不同的解，设好解在所有解中占的比率为u，则v个解存在好解的概率为1－(1－u)v．这说明若能保证搜索到足够多的不同的解，那么能搜索到足够好解的概率接近1．

基于该思想，文中设计禁忌表TL2来禁忌迭代搜索过程中出现过的历史局部最优解，使得当前解尽量不陷入被禁忌的局部最优解，以避免重复搜索．

禁忌表TL2包括禁忌的解序列S和对应的目标函数值f(S)，TL2的规模会随着搜索的进行而增大．在判断某个解是否被TL2禁忌时，考虑到直接将解序列与TL2中所有存放的解相比较计算复杂，为了提高算法的效率，首先对解的目标值进行判断．若目标值未被禁忌，则解序列一定不同;若目标值相同，再完整比较解序列是否一致．经判断后，若解被TL2禁忌，则将其舍弃，在余下邻域中继续搜索．

2．5 RLS

文中引入一种基于插入邻域的RLS搜索策略，当迭代搜索陷入局部最优时，以一定概率P对解实行变换，使得搜索尽量逃离局部最优．RLS是一种重复插入的局部搜索方法［12］，对解为序列或集合的优化问题较为有效．由于单个元器件的插入移动会改变一系列取贴循环的组成，对解的整体结构造成较大的改变．因此文中将解分成N部分，每部分是一个取贴循环的拾取序列．RLS直接对每个取贴循环进行重复插入，而不是对每个元器件实施变换，如图6所示．

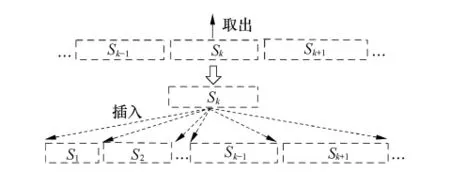
图6 基于取贴循环插入的RLSFig．6 RLS based on inserting mounting circles

设当前解序列 Sc=(S1，S2，…，SN)，对应目标函数值为fc，对Sc应用RLS搜索策略进行以取贴循环为单位的变换，步骤如下:

1)对当前解进行扰动

(1)随机选择r个取贴循环，并按照取贴循环在解序列中的位置进行升序排序，得到(J1，J2，…，Jr)，对应在序列中的位置为(p［1］，p［2］，…，p［r］)，令 h:=1．

(2)从当前序列中取出Jh并插入到p［h］所在位置之前的所有位置，得到p［h］个新序列，选取具有最小目标函数值fnew的新解Snew．

(3)若 fnew＜ fc，则 fc:=fnew，Sc:=Snew．h:=h+1．若h≤r，则返回步骤(1);否则输出扰动后的解Sc．

2)基于参考解的搜索

(1)随机生成拾取序列并作为参考序列R，令h:=1，k:=1．

(2)h:=h%N(%为取余运算)，将 R［h］从序列 Sc中移出，分别插入到位置 0，1，…，h，得到解集对应的序列为Snew．

(3)若 fnew＜fc，则更新 fc:=fnew，Sc:=Snew，k:=1;否则 k:=k+1．

(4)h:=h+1，若 k≤N，则返回步骤(2);否则基于参考解的搜索结束，输出Sc．

通过插入移动，RLS将参考解的特性融入到当前解中．参考解的分散性强时，有助于提高算法的分散搜索能力．拾取序列对应的贴装序列则在计算目标值时，通过全枚举小规模TSP问题的解获得．

2．6 算法步骤

基于RLS的改进TS算法步骤如下:

1)运用2．2节中所描述的方法产生初始解，并设为当前解Sc和当前最好解Sbest，对应目标函数值为fc和fbest．设置最大迭代步数itermax、最大未改进迭代步数 Un_itermax、禁忌表TL1的长度L、进行 RLS变换的概率P，循环次数iter=0，未改进迭代次数Un_iter=0．

2)搜索当前解的交换邻域，记录最好的邻解Snei和未被TL1和TL2禁忌的邻解Sl．

3)判断藐视准则是否成立，若f(Snei)＜fbest，则fbest:=f(Snei)，Sbest:=Snei，Sc:=Snei;否则 Sc:=Sl．

4)生成随机数 r'～［0，1］，若 r'＜ P，则按 2．5节中的RLS方法对解Sc进行变换．

5)若Sbest在本次迭代中更新，则Un_iter:=0，否则Un_iter:=Un_iter+1．将禁忌表TL1中非0元素减1，并将新禁忌的两个点的禁忌长度设定为L，将Sc及其fc写入禁忌表TL2中，令iter:=iter+1．

6)若Un_iter＞Un_itermax(达到最大未改进最好解的迭代次数)或 iter＞itermax(达到最大迭代次数)，则算法终止，输出结果Sbest和f(Sbest);否则转步骤2)．

3 实验及算法性能分析

文中算法使用VC++6．0软件编程，并在内存为4096MB的FUJITSU计算机上运行．测试实例是20块PCB的实际贴装数据，对每个数据均测试10次取结果的平均值．实验对象为四贴装头的拱架式贴片机，贴装头间距为16mm，两侧分别有50个槽位，喂料器分配给定，禁忌表TL1长度L=12，最大迭代步数itermax=200，最大未改进迭代步数Un_itermax=20，RLS变换的概率P=0．2．为验证文中算法的有效性，将算法计算结果与使用蚁群 －混合蛙跳算法［6］、参数相同情况下不带RLS搜索策略的改进TS算法的结果进行了比较，如表1所示，算例运行时间见表2．

表1表明，使用文中算法求解贴装顺序优化问题得到的结果优于蚁群－混合蛙跳算法［6］的求解结果，20块PCB的解平均值提高了16．17%．文献［6］算法将元器件的贴装顺序作为解序列，而元器件的拾取顺序取与贴装顺序相同的序列，该处理方法可能导致取贴循环内贴装头在喂料槽上来回移动的次数增加，从而使总路径增加．文中算法对这两个序列同时优化，求解方法更为有效．根据表1，对于元器件数量超过100的后12组数据，RLS搜索策略能带来平均1．14%的改进，证明了文中算法的性能更优，在解决规模较大的问题上效果更突出．

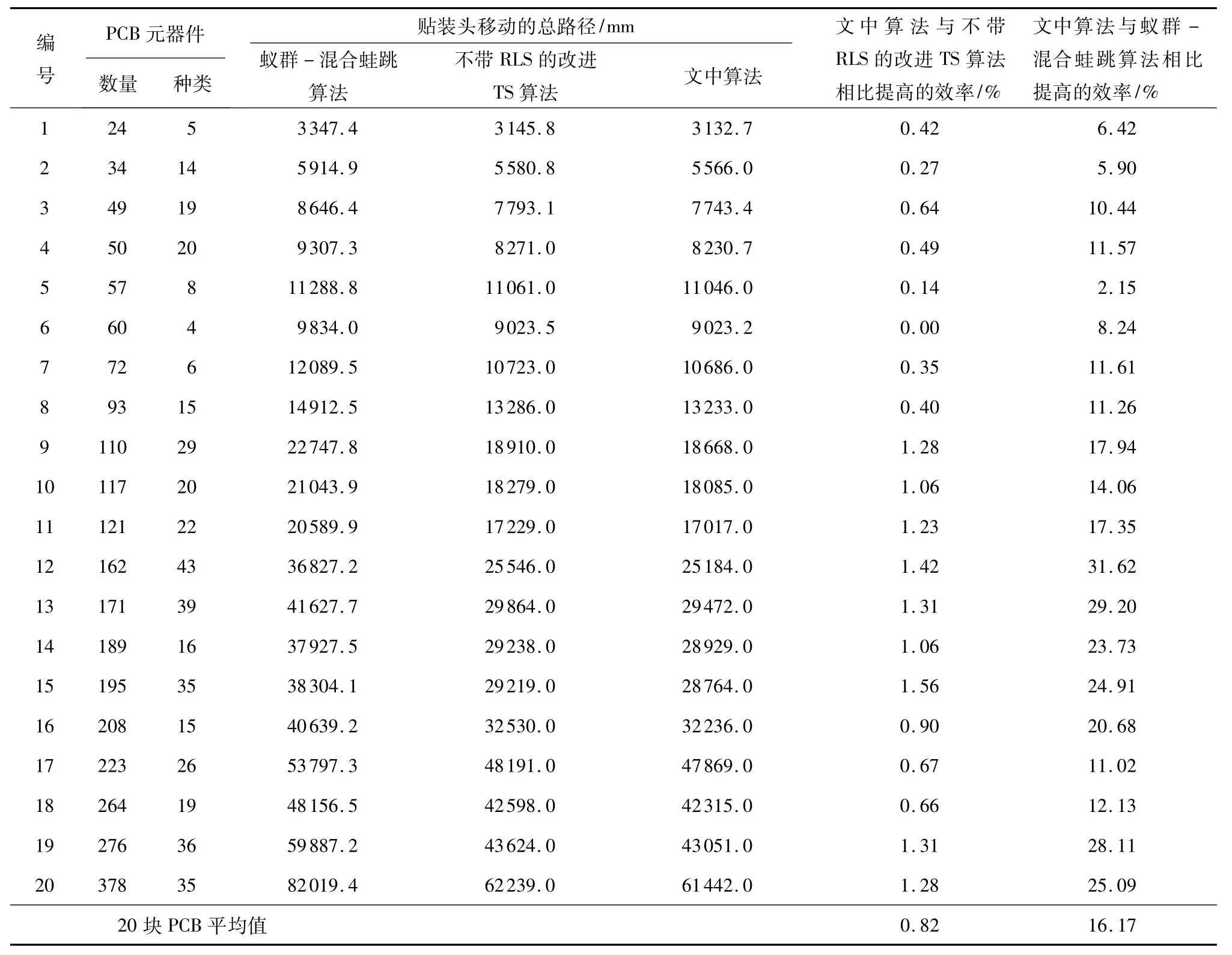
表1 几种算法的实验结果比较Table 1 Comparison of the experimental results obtained by several algorithms

根据表2，尽管文中算法的运行时间会随着问题规模的增大而增加，但当元器件数量为378时求取一个解所用的时间约为43．043 s，因此算法的计算时间在实际应用中是可以接受的．

表2 每个实例的运行时间Table 2 Running time for each instance

4 结语

文中针对拱架式贴片机贴装顺序优化问题，建立了数学规划模型，提出了一种基于RLS的改进TS算法．在该算法中，应用了最近邻算法生成初始解，采用了交换邻域结构，设计了双禁忌表来避免迂回搜索，并引入以取贴循环为单位的RLS变换策略来提高算法突破局部最优的能力．通过对实际生产的20块PCB数据进行仿真计算，并将结果与文献计算结果作比较，结果表明文中提出的改进TS算法能更有效地解决贴片机贴装顺序优化问题．

［1］ Michael O B，Michael J M．Sequencing of insertions in printed circuit board assembly ［J］．Operations Research in Manufacturing，1988，36(2):192－201．

［2］ LeipäläT，Nevalainen O．Optimization of the movements of a component placement machine［J］．European Journal of Operational Research，1989，38(2):167－177．

［3］ 曾又姣，金烨．基于遗传算法的贴片机贴装顺序优化［J］．计算机集成制造系统，2004，10(2):205－208．Zeng You－jiao，Jin Ye．Component placement sequence optimization for surface mounting machine based on genetic algorithm ［J］．Computer Integrated Manufacturing Systems，2004，10(2):205－208．

［4］ 杜轩，李宗斌，高新勤，等．基于遗传算法的转塔式贴片机贴装过程优化［J］．西安交通大学学报，2008，42(3):295－299．Du Xuan，Li Zong－bin，Gao Xin－qin，et al．Component placement process optimization for chip shooter machine based on genetic algorithm［J］．Journal of Xi’an Jiaotong University，2008，42(3):295－299．

［5］ 朱光宇，林蔚清．基于改进混合蛙跳算法的贴片机贴装顺序优化 ［J］．中国工程机械报，2008，6(4):428－432．Zhu Guang－yu，Lin Wei－qing．Mounting sequential optimization on surface mounting machine using improved hybrid frog－jumping algorithm ［J］．Chinese Journal of Construction Machinery，2008，6(4):428－432．

［6］ 陈铁梅，罗家祥，胡跃明．基于蚁群－混合蛙跳算法的贴片机贴装顺序优化［J］．控制理论与应用，2011，28(12):1813－1820．Chen Tie－mei，Luo Jia－xiang，Hu Yue－ming．Mounting sequence optimization on surface mounting machine using ant－colony algorithm and shuffled frog－leaping algorithm［J］．Journal of Control Theory ＆ Applications，2011，28(12):1813－1820．

［7］ 袁鹏，刘海明，胡跃明．基于伞布搜索法的贴片机贴装顺序优化算法［J］．电子工艺技术，2007，28(6):316－320．Yuan Peng，Liu Hai－ming，Hu Yue－ming．Scatter searching algorithm for multi－headed surface mounter ［J］．Electronics Process Technology，2007，28(6):316－320．

［8］ 俞国燕，郑时雄，刘桂雄，等．复杂工程问题全局优化算法研究［J］．华南理工大学学报:自然科学版，2000，28(8):104－110．Yu Guo－yan，Zheng Shi－xiong，Liu Gui－xiong，et al．Study on global optimization algorithms for complex engineering problem ［J］．Journal of South China University of Technology:Natural Science Edition，2000，28(8):104－110．

［9］ Glover F．Future paths for integer programming and links to artificial intelligence［J］．Computers and Operations Research，1986，13(5):533－549．

［10］ Glover F，Gutin G，Yeo A，et al．Construction heuristics for the asymmetric TSP ［J］．European Journal of Operational Research，2001，129(3):555－568．

［11］ Edward Lau T W，Ho Y C．Universal alignment probabilities and subset selection for ordinal optimization ［J］．Journal of Optimization Theory and Applications，1997，93(3):455－489．

［12］ Tasgetiren F，Pan Q K，Liang Y C．A discrete differential evolution algorithm for the single machine total weighted tardiness problem with sequence dependent setup times［J］．Computers and Operations Research，2009，36(6):1900－1915．