基于密度估计的异常电力负荷数据辨识与修正*

陈亮 文福拴 童述林

(1．华南理工大学电力学院，广东广州510640;2．广东省 电力调度中心，广东广州510600;3．浙江大学 电气工程学院，浙江杭州310027)

来源于SCADA系统的电力负荷数据由于信道错误、冲击负荷以及突发事故等原因会产生一些异常数据，这不仅影响负荷预测的精度［1-2］，而且对有关的系统分析任务如空调负荷的测算和分析［3］也会带来负面影响．此外，高质量的负荷数据与准确的负荷预测结果是电力系统规划和运行调度的重要根据，且在未来的智能电网中这点尤为明显［4］．例如，智能电表作为智能电网的重要组成部分，对负荷数据质量要求很高．另一方面，在针对未来大量电动汽车广泛接入电力系统后的智能充放电方案的实现中［5］，也需要事先预测次日负荷，然后配合分时充放电价格机制，引导电动汽车用户在谷荷区段接入电力系统充电，而在峰荷区段向系统反向放电，从而达到缩小系统负荷峰谷差、提高设备利用率的效果，高质量的负荷数据对此也具有重要作用．因此，有必要对负荷数据中存在的异常数据进行辨识和修正．

到目前为止，电力负荷异常数据的辨识与修正方面，国内外已经做了相当多的研究．文献［6］中提出用学习矢量量化(LVQ)方法对异常负荷数据进行剔除，基本思路是将负荷数据视为若干组矢量，若某个矢量中有一个分量为异常数据，则将整个矢量剔除，这种做法有可能造成大量可用信息丢失，无法准确定位坏数据．文献［7］中采用灰色理论与参数估计相结合的方法来检测异常负荷数据;由于参数估计是复杂的非线性优化问题，一般不能保证获得全局最优解．文献［8］中提出对辨识出的异常负荷数据用扩展短期负荷预测结果进行修正，该方法对单个异常负荷数据的辨识与修正较为有效，但对连续异常负荷数据的效果不佳．文献［9］中根据SCADA系统中的冗余数据，利用连续日期相同时段负荷数据的均值和方差来进行辨识与修正;这种方法对由于数据采集系统故障引起的异常数据比较有效，在处理负荷异常波动方面的效果则不够明显．文献［10-11］中均采用人工神经元网络来进行异常数据识别，但这种方法需要的训练时间很长．文献［12］中采用ART2人工神经元网络模型进行异常负荷数据的识别与调整，这种方法虽然避免了前馈人工神经元网络模型容易陷入局部最优解的问题，但需要事先对负荷曲线进行分类并提取特征曲线．文献［13］中借鉴计算统计学中的等高线图法，采用系统聚类方法与传统的t检验法相结合，对异常数据进行辨识与修正．

到目前为止，在异常负荷数据的辨识与修正方面，研究工作大都只单独考虑负荷的横向连续性或纵向连续性，即在一个维度中进行处理，具有一定的局限性．有鉴于此，文中同时考虑了负荷的横向连续性与纵向连续性．具体地讲，首先把每天96点负荷曲线数据按日期排列成二维数据集，然后使用密度估计方法［14］，从整体上对异常数据进行识别，最后对识别出的异常数据进行修正．文中还采用广东省实际电力负荷数据做了计算，仿真结果表明这种方法是有效的．

1 基于密度估计的异常数据识别与修正

首先对数据密度［14］进行估算，然后依据所得密度进行异常负荷数据识别与修正．

1．1 数据密度估计方法描述

数据密度估计方法的基本原理如下:

(1)假设有一个数据点总数为M的二维数据集Z(如图1(a)中的圆点所示)．

(2)产生一个称为种子群的数据集 S(如图1(a)中的圆圈所示)，其所含的种子个数N需事先确定，且需保证各个种子与其相邻种子之间的距离恒等，此外还需要保证种子群的范围能够包含数据集Z．

(3)每个数据点 zj(j∈{1，2，…，M})均附有一个初值为0的种子吸附计数器ci，用于累计该数据点吸附的种子数目．

(4)对于每个种子 si(i∈{1，2，…，N})分别计算它与数据集Z的各个数据点之间的距离，假设距离种子si最近的数据点为zk．采用欧式距离确定距离种子si的最近数据点zk的排序(即下标k)的过程可表示如下:

式中，i∈{1，2，…，N}，j∈{1，2，…，M}，arg 是argument的缩写．式(1)的含义为取使目标函数值最小时的j值为k．

(5)依据式(1)确定距离种子si最近的数据点zk，将该数据点所附带的种子吸附计数器ck加1．如果存在p个数据点与种子si距离相等且均为最近，则等比例地分配给这些数据点，即距离最近的每个数据点的种子吸附计数器均累加1/p．

(6)对于种子群S中的每个种子均按式(1)确定距其最近的数据点，然后按上述规则更新相应数据点种子吸附计数器的值，直至所有种子都计算完为止．

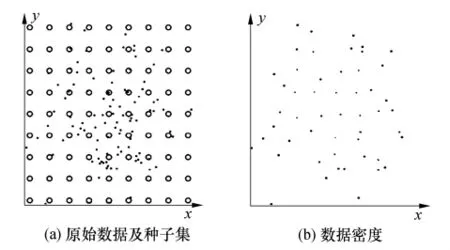
图1 数据密度简化原理图Fig．1 Simplified data density scheme

1．2 识别原理

前已述及，每个数据点附带一个种子吸附计数器，用来累计每个数据点吸附的种子数目．这样，就有以下两点结论:

(1)如果某个数据点的种子吸附计数器的值大，则表明该数据点吸附的种子多，即该数据点的邻域内与其竞争分享这些种子的数据点不多，该数据点密度低;

(2)若某一数据点的邻域内存在许多数据点，那么该数据点与其周围的数据点在吸附种子时就存在较为激烈的竞争，每个数据点所吸附的种子数目就较少．

以图1(b)为例，其中小点表示密度较大的数据点，大点则表示密度相对较小的数据点．

数据点的密度较低表示在其邻域内出现数据点的概率较小，这样就可把种子吸附计数器值高于某个设定值的数据点归为不良数据，在文中把此设定值称为种子吸附阈值．

1．3 参数确定

该算法中需确定两个参数，即种子数目和种子吸附阈值．

1．3．1 种子数目的确定

(1)计算每个数据点与其它数据点之间的最短距离:

式中:i，j∈{1，2，…，M}且 j≠i．

(2)按下式确定所有数据点与其它数据点间最短距离的均值d，并将其作为种子点与其邻近种子之间的距离:

(4)在确定了种子间距离和种子范围之后，即可计算出种子数目．

1．3．2 种子吸附阈值的确定

种子吸附阈值可根据所得全部种子吸附值的总体分布来确定．这里采用下述方法:先把种子吸附值按从大到小的次序排列，给定某个百分位数作为种子吸附阈值．在实际应用中，可以视具体情况灵活调整该阈值，以取得好的效果．

(3)确定种子范围，即为了确保种子范围能够包括所有数据点，假设数据集某维的取值范围为zmin～zmax，则种子集此维的上下边界 smax与 smin应满足:

1．4 异常数据的修正

对识别出来的需要修正的某时段负荷可以用其前m个同类型日相同时段的负荷加权平均值来修正［15］，整个过程按照时间顺序进行，当检测到异常数据时立即修正．修正公式如下:

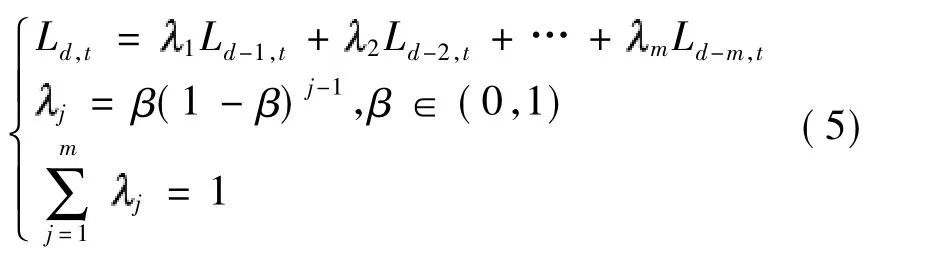
式中:Ld，t为第 d 天时段 t的负荷数据;Ld－m，t为其前第d－m个同日期类型日时段t的负荷;m为权值系数，用于表征 Ld－m，t对 Ld，t的影响程度;β 为平滑系数．

2 负荷数据预处理流程

文中对负荷数据进行预处理的步骤可描述如下．

步骤1 选择待预测日前n天的每天96点负荷数据作为样本，并形成n行96列的二维数据集Z，其数据点个数M=96n;

步骤2 确定种子数目N;

步骤3 生成一个恒等间距的种子群S;

步骤4 初始化数据点的种子吸附计数器ck=0;

步骤5 计算种子si与所有数据点间的距离，找到距离该种子最近的数据点，并更新该数据点的种子吸附计数器ck的值;

步骤6 重复步骤5，直至完成对所有种子的计算处理;

步骤7 确定种子吸附阈值;

步骤8 用如此得到的吸附阈值进行异常数据识别并按式(5)对其进行修正．

上述步骤可用图2来表示．

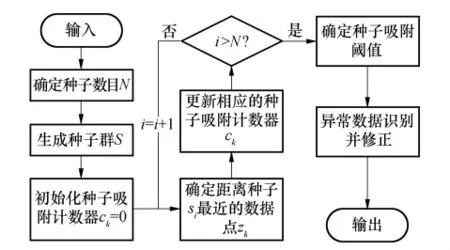
图2 数据处理流程Fig．2 Flowchart of data processing

3 实例结果与分析

选取广东省2009年统调负荷20天每日96点负荷数据共1920个数据点作为样本，人为设置了24个数据突变点与缺失点，这样异常数据率为24/1920=1．25%．把种子吸附值按从大到小进行排列，取第1．25百分位数(根据24/1920=1．25%设置)作为种子吸附阈值．然后，针对所识别出的异常数据，采用最近5个相同日期类型的同时段负荷作为修正时的历史参考负荷数据，从中选取其温度与需修正时段温度最为接近的3个;取平滑系数β为0．5，按“近大远小”的原则，且满足式(5)中的约束，取1=0．5，2=0．25，3=0．25．下面从两个方面对负荷数据预处理的效果进行分析．

3．1 负荷数据预处理前后对比

这里将前述的在两个维度中处理的方法与文献［15］中提出的在一个维度中处理的方法(改进的数据横向比较法)进行比较．对于这两种方法，均对选取的样本数据进行了异常数据的辨识与修正．对比结果见表1．可以看出，基于密度估计的方法能很好地辨识异常负荷数据点并给予适当修正，其修正负荷的相对误差在5%以内，且较改进的数据横向比较法要好些．

对使用密度估计的方法进行预处理前后的负荷数据用图形直观显示，如图3所示．可以看出，采用负荷数据预处理能对异常数据进行很好地识别和修正．

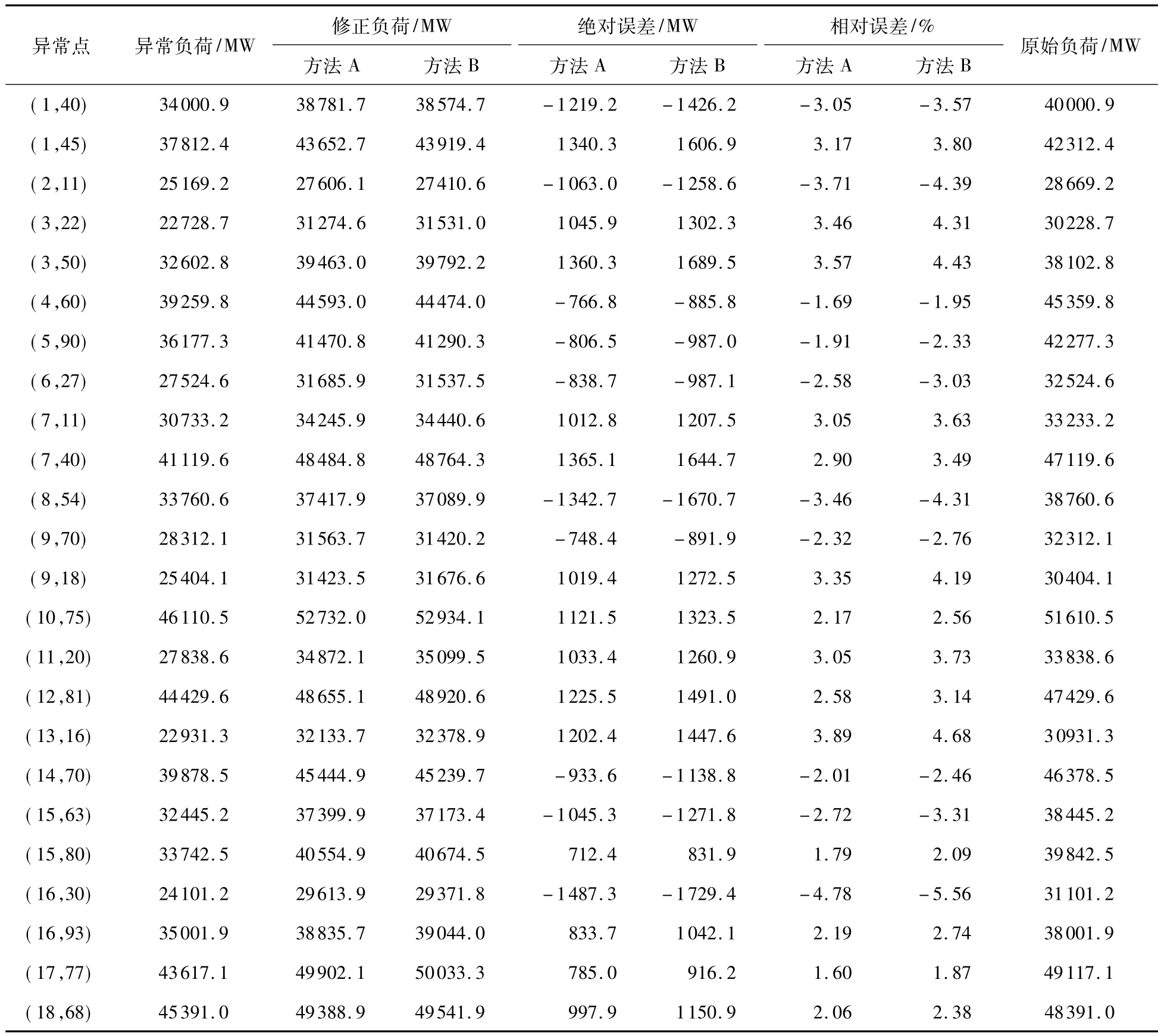
表1 两种方法下的异常数据识别与修正效果对比1)Table 1 Comparison of identification and correction of abnormal electric load data when using two methods

1)表中异常点(m，n)表示选取数据样本里第m(1≤m≤20)天的第n(1≤n≤96)个时刻，方法A和B分别表示文中所述方法与文献［15］中改进的数据横向比较法．

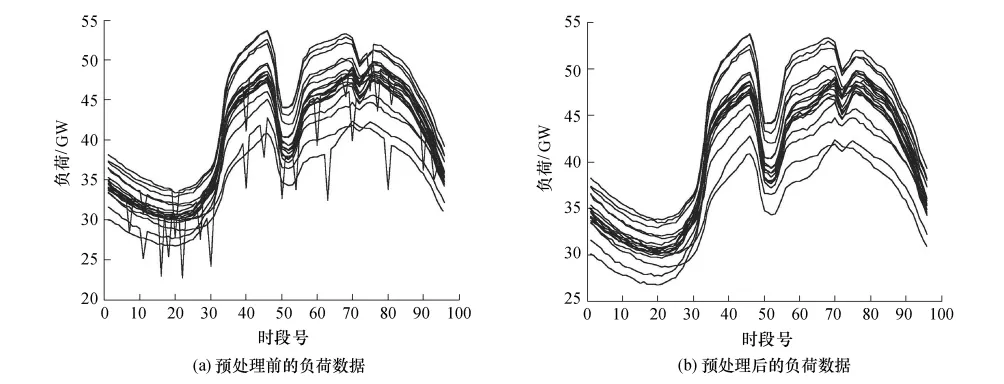
图3 预处理前后负荷数据对比Fig．3 Comparison of load data before and after preprocessing

3．2 日负荷预测准确率评价

由于负荷数据序列一般为含有增长趋势和周期变化趋势的非平稳序列，这里采用差分自回归移动平均模型［16］(ARIMA)，分别用预处理前后的负荷样本数据进行预测．预测效果的评价指标采用日预测准确率，其定义如下:

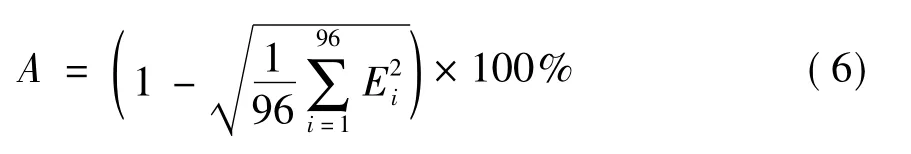
式中，Ei为预测日第i个时段的相对误差，A为预测日的日预测准确率．

所采用的ARIMA模型的参数确定思想如下:(1)对原始序列进行差分运算，消除非平稳序列的增长趋势;(2)用周期性差分消除序列的周期变化趋势，得到平稳序列;(3)用ARMA模型对得到的平稳序列进行拟合，其参数确定方法采用长自回归计算残差法［16］．

一周内的负荷预测效果见表2．由表2可知，采用预处理后的数据，平均日预测准确率为93．47%，较未经处理时的91．80%提高了1．67%．可见，对负荷数据进行预处理后，预测精度有明显提高．

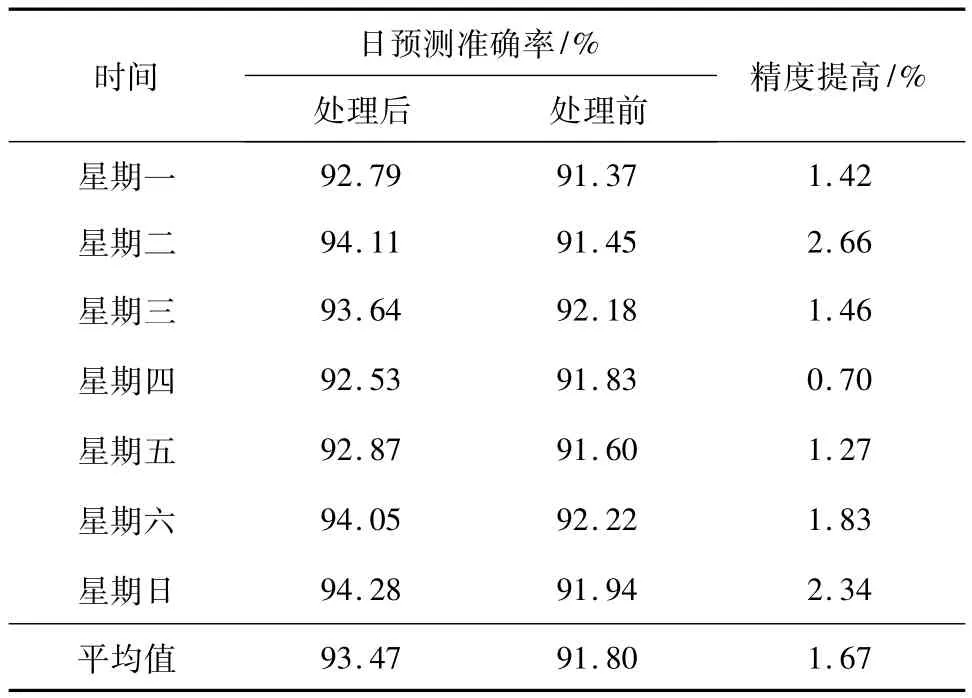
表2 预处理前后日预测准确率对比Table 2 Comparison of load forecast accuracy before and after load data preprocessing

4 结语

基于密度估计的异常数据识别与修正方法可以有效识别与修正连续突变或连续缺失的数据点，且识别过程是基于原始数据整体进行的，避免了现有的横向比较法的缺点．用广东省电力系统的实际数据对所提出的方法进行的验证表明，文中方法可行且有效．

即便如此，但还有一类典型异常数据，即由于信道传输等引起的噪声数据，对其进行去噪还需进一步的研究．

［1］ 康重庆，夏清，张伯明．电力系统负荷预测研究综述与发展方向的探讨 ［J］．电力系统自动化，2004，28(17):1-11．Kang Chong-qing，Xia Qing，Zhang Bo-ming．Review of power system load forecasting and its development［J］．Automation of Electric Power Systems，2004，28(17):1-11．

［2］ 康重庆，夏清，刘梅．电力系统负荷预测［M］．北京:中国电力出版社，2007:84-86．

［3］ 童述林，文福拴．节能减排环境下广东省年最大降温负荷的测算与分析［J］．华北电力大学学报:自然科学版，2010，37(5):32-37．Tong Shu-lin，Wen Fu-shuan．Calculation and analysis of the annual maximum high-temperature related load in the energy saving and emission reduction environment in Guangdong Province［J］．Journal of North China Electric Power University:Natural Science，2010，37(5):32-37．

［4］ Chen Ji-yi，Li Wen-yuan，Lau Adriel，et al．Automated load curve data cleansing in power systems［J］．IEEE Trans on Smart Grids，2010，1(2):213-221．

［5］ Denholm P，Short W．Evaluation of utility system impacts and benefits of optimally dispatched plug-in hybrid electricvehicles ［EB/OL］．［2006-10-31］．http://www．nrel．gov/docs/fy07osti/40293．pdf．

［6］ Karayiannis N B．An axiomatic approach to soft learning vector quantization and clustering［J］．IEEE Trans on Neural Networks，1999，10(5):1015-1019．

［7］ 康重庆，夏清，相年德．灰色系统的参数估计与不良数据辨识 ［J］．清华大学学报:自然科学版，1997，37(4):72-75．Kang Chong-qing，Xia Qing，Xiang Nian-de．Parameter estimation and bad data identification of grey systems［J］．Journal of Tsinghua University:Science ＆ Technology，1997，37(4):72-75．

［8］ 莫维仁，张伯明，孙宏斌，等．扩展短期负荷预测方法的应用［J］．电网技术，2003，27(5):6-9．Mo Wei-ren，Zhang Bo-ming，Sun Hong-bin，et al．Application of extended short-term load forecasting［J］．Power System Technology，2003，27(5):6-9．

［9］ 叶锋，何桦，顾全，等．EMS中负荷预测不良数据的辨识与修正 ［J］．电力系统自动化，2006，30(15):85-88．Ye Feng，He Hua，Gu Quan，et al．Bad data identification and correction for load forecasting in energy management system［J］．Automation of Electric Power Systems，2006，30(15):85-88．

［10］ 张国江，邱家驹，李继红．基于人工神经网络的电力负荷坏数据辨识与调整［J］．中国电机工程学报，2001，21(8):104-108．Zhang Guo-jiang，Qiu Jia-ju，Li Ji-hong．Outlier identification and justification based on neural network［J］．Proceedings of the CSEE，2001，21(8):104-108．

［11］ 张晓星，程其云，周湶，等．基于数据挖掘的电力负荷脏数据动态智能清洗［J］．电力系统自动化，2005，29(8):60-64．Zhang Xiao-xing，Cheng Qi-yun，Zhou Quan，et al．Dynamic intelligent cleaning for dirty electric load data based on data mining［J］．Automation of Electric Power Systems，2005，29(8):60-64．

［12］ 顾民，葛良全，秦健．基于改进ART2网络的电力负荷脏数据辨识与调整［J］．电力系统自动化，2007，31(16):70-74．Gu Min，Ge Liang-quan，Qin Jian．Identification and justification of dirty electric load data based on modified ART2 network ［J］．Automation of Electric Power Systems，2007，31(16):70-74．

［13］ 陈建华，戴铁潮，张宁，等．确定性合同分解中异常负荷数据的辨识与修正［J］．电力系统自动化，2009，33(6):21-24，43．Chen Jian-hua，Dai Tie-chao，Zhang Ning，et al．Load outlier identification and correction for deterministic contract decomposition ［J］．Automation of Electric Power Systems，2009，33(6):21-24，43．

［14］ 王扬．一种新颖的基于密度的袪噪声方法［J］．自动化学报，2010，36(2):333-346．Wang Yang．A novel algorithm for outlier removal based on density．［J］ Acta Automatica Sinica，2010，36(2):333-346．

［15］ 李光珍，刘文颖，云会周，等．母线负荷预测中样本数据预处理的新方法 ［J］．电网技术，2010，34(2):149-154．Li Guang-zhen，Liu Wen-ying，Yun Hui-zhou，et al．A new data preprocessing method for bus load forecasting［J］．Power System Technology，2010，34(2):149-154．

［16］ 杨叔子，吴雅，轩建平，等．时间序列分析的工程应用［M］．武汉:华中科技大学出版社，2007:236-237．